Вступ

Деформація прямого поперечного згинання стержня виникає у тому разі, якщо до нього в площинах, які проходять через ось стержня, прикладені пари сил (моменти), сили, перпендикулярні до цієї осі.

Балки – це стержні, які працюють на згинання. Балки є найбільш розповсюдженими елементами споруд, конструкцій і деталей машин, які сприймають навантаження від інших елементів і передають їх до опор. Таким чином на балку діють прикладене навантаження і реакції опор. Опори балки відносяться до одного з таких трьох типів: шарнірно-рухома опора, шарнірно-нерухома опора, защемлений кінець (консольна балка).

На згинання працюють вали, вагоні осі, балки міжповерхового перекриття, різці, зуб’я коліс передач і таке інше. Багато авіаційних конструкцій розраховуються на міцність, як балки. Це такі елементи фюзеляжу і крила літака, як нервюри, стрингери, лонжерони. На згинання розраховуються оперення літака. Крило літака розраховується на згинання під дією навантаження: аеродинамічного і масового. Основні види розрахунків на міцність при згинанні це: перевірочний і проектувальний.

Перевірочний розрахунок передбачає порівняння максимальної розрахункової напруги з допустимою.

Проектувальний розрахунок передбачає знаходження оптимальних і економічних розмірів поперечного перерізу конструкції (деталі) за умови міцності на згинання.

Перевірочний і проектувальний розрахунки виконуються для небезпечного перерізу балки, для визначення якого треба вміти будувати епюри згинальних моментів і поперечних сил за правилами розділу «Основи опору матеріалів».

1. Розрахункова частина

   1. Визначення величини та напрямку опорних реакцій балки

Необхідні для розрахунку дані:

Таблиця 1

Р, кН	М, кН·м	q, кН\м	а, м	с, м	d, м
30	40	5	2	1	2

Для визначення величини і напрямку опорних реакцій балки слід додержуватись такої послідовності:

• Зобразити розрахункову схему балки у довільно обраному масштабі і прикласти до неї задане навантаження;

• Прикласти до балки невідомі реакції опор, спрямувати їх попередньо вверх. У кожній опорі виникає по одній реакції;

• Скласти рівняння рівноваги статики, прирівнявши алгебраїчні суми моментів усіх сил відносно опорних точок балки до нуля. Рівномірне розподілене навантаження слід замінити однією рівнодіючою силою, яку прикласти в середині розподіленого навантаження і розглядати як зосереджену силу. При визначенні моментів сил відносно точки слід бути уважними з встановленням знаку моменту і додержуватись певного правила;

• Знайти модулі невідомих реакцій, вирішивши рівняння рівноваги.

Спрямуємо реакції опор балки попередньо вверх, і для їх визначення складаємо рівняння статики. Рівномірно розподілене навантаження інтенсивністю q на довжині а. Замінимо однією рівнодіючою силою, яку прикладаємо у середині довжини навантаження. Ця рівнодіюча дорівнює q·a

Для визначення реакції R_B складаємо алгебраїчну суму моментів всіх сил відносно точки А, яка дорівнює нулю:

При визначенні моменту приймаємо такі знаки: проти часової стрілки – «+», за часовою – «-».

Для визначення реакції R_А складаємо алгебраїчну суму моментів всіх сил відносно точки В, яка дорівнює нулю:

Перевірка знайдених реакцій:

Модулі реакцій знайдені вірно, але напрямок реакції R_A слід змінити на протилежний. Реакція R_A спрямована вниз.

2. Побудова епюр згинальних моментів і поперечних сил на кожній ділянці балки і перевірка правильності побудови цих епюр

Для побудови епюр згинальних моментів і поперечних сил треба розбити балку на дільниці. Границями дільниць є точки прикладання навантажень на балку (характерні точки).

Визначаючи згинальні моменти і поперечні сили у довільному перерізі кожної дільниці за методом перерізів, слід використовувати правила і рекомендації з розділу: основи опору матеріалів.

При визначенні згинальних моментів у довільному перерізі з довільною координатою ділянці слід сумістити початок відліку з характерною точкою дільниці (початок чи кінець). При визначенні поперечних сил у довільному перерізі дільниці слід пам’ятати, що правила знаків для сил ліворуч і праворуч перерізу протилежні.

Зробимо есзік балки у довільно обраному масштабі та прикладемо до неї задане навантаження і правильно визначені реакції.

Розбиймо балку на окремі дільниці. Балка має три дільниці 1- АС, 2- ЕА, 3- ВЕ.

Для визначення згинальних моментів у довільних перерізах дільниць застосовуємо засіб перерізів, та правило згідно якого згинальний момент у довільному перерізі балки дорівнює алгебраїчній сумі моментів всіх сил. Або пар сил, які діють на залишену частину відносно центру ваги даного перерізу.

1–дільниця 0 ≤ Z₁ ≤ 2м;

хай z₁=0, тоді:

хай z₁=2 м, тоді:

хай z₁=1 м, тоді:

2–дільниця 0 ≤ Z₂ ≤ 1м;

хай z₂=0 м, тоді:

хай z₂=1 м, тоді:

3–дільниця 0 ≤ Z₃ ≤ 2м;

хай z₃=0 м, тоді:

хай z₃=2 м, тоді:

Епюри згинальних моментів і поперечних сил будують у довільно обраному масштабі. Знайдені значення відкладають від бази епюри (нульової лінії). Зі знаком «+» – вверх, зі знаком «–» – вниз. Епюри штрихують лініями, які перпендикулярні до бази. Якщо на дільниці поперечна сила Q змінює знак, то слід знайти z, при якому поперечна сила дорівнює нулю з рівняння Q_Z = 0 для даної дільниці, а також підрахувати значення згинального моменту M_Z у цьому перерізі. Правильність побудови епюр згинальних моментів і поперечних сил слід перевірити за правилами:

• на дільниці з рівномірно-розподіленим навантаженням епюра згинальних моментів – парабола опуклістю назустріч навантаженню;

• під моментом на епюрі згинальних моментів повинен бути стрибок, який дорівнює цьому моменту;

• під силою на епюрі поперечних сил повинен бути стрибок, який дорівнюватиме цій силі;

• якщо на дільниці згинальний момент зростає зліва направо, то поперечна сила на цій дільниці має знак «+» і навпаки.

Для побудови епюри поперечних сил визначаємо поперечні сили у довільних перерізах балки використовуючи засіб перерізів і правила знаків.

1-дільниця 0≤z₁≤2 м;

Якщо z₁=0, то:

2-дільниця 0≤z₂≤1 м;

3-дільниця 0≤z₃≤2 м;

Будуємо епюру згинальних моментів відкладаючи знайдені значення у довільно обраному масштабі від бази (осі) епюри, яку проведемо паралельно осі балки.

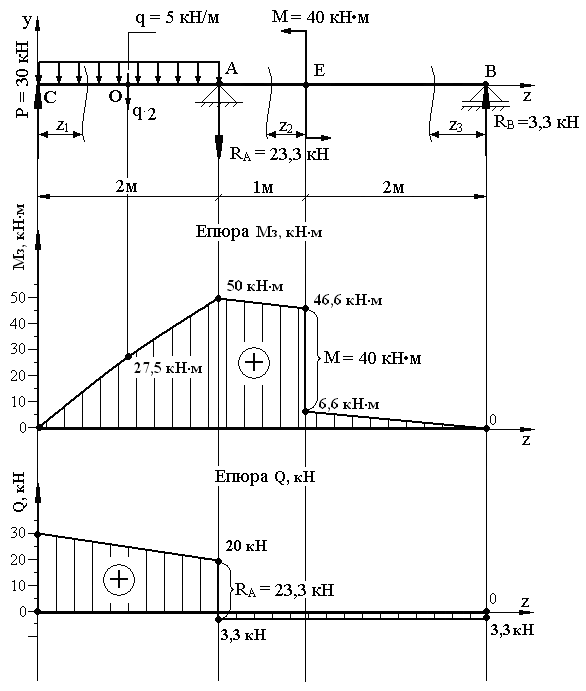
Перевіримо правильність побудованих епюр згинальних моментів і поперечних сил.

На дільниці СА згинальних моментів зображується параболою опуклістю на зустріч навантаженою. На дільницях АЕ та ВЕ – прямі нахилені лінії до осі балки. Під зовнішнім моментом на епюрі М_з маємо стрибок, що дорівнює цьому моментові.

На епюрі поперечних сил маємо стрибок, який стався під силою і дорівнює цій силі.

На дільниці АЕ спадає зліва направо, тому поперечна сила на цій ділянці має знак «–». На дільниці ЕВ згинальний момент спадає зліва направо, тому поперечна сила на цій дільниці має знак «–».

Якщо на дільниці з рівномірно розподіленим навантаженням поперечна сила змінює знак через нуль то згинальний момент в цьому перерізі має максимальне значення (екстремальне).

Результати обчислень згинальних моментів і поперечних сил заносимо в таблицю 2.

Таблиця 2

Дільниця	Z, м	Мз, Кн·м		Qз, кН
1 (СА)	0≤z1≤2	0	50	30	20
2 (АЕ)	0≤z2≤1	50	46,6	-3,3	-3,3
3 (ВЕ)	0≤z3≤2	6,6	0	-3,3	-3,3