17. Градиентный метод.

Градиентные методы — численные методы решения с помощью градиента задач, сводящихся к нахождению экстремумов функции.

градиент Ñf(x), как вектор, указывает направление возрастания функции f в точке x (любое достаточно малое перемещение из точки x в направлении вектора Ñf(x) увеличивает значение функции f). Это замечательное свойство положено в основу многих вычислительных методов. Итеративные методы, в которых направление rx определяется при помощи градиента Ñf(x) (в задачах на максимум) и антиградиента -Ñf(x) (в задачах на минимум), называются градиентными методами. К числу градиентных можно отнести метод Ньютона, в котором rk = -Ñf(x), ak = [Ñ2f(xk)]-1, а также методы наискорейшего спуска (см. там же), в которых длина шага определяется в результате решения оптимизационной задачи в направлении антиградиента.

Суть градиентного метода ( рис. 18, а) состоит в чередовании процедур определения градиента целевой функции и рабочего шага. Каждый рабочий шаг анализируется на успешность и срыв. 

18.условие окончание поиска оптимума целевой функции.

Условия окончания поиска.

1)

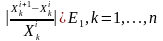
2)

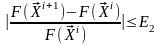
3) 1)+2)

4)

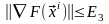
5) Ограничение числа итераций.

20. Метод Эйлера.

В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Идея метода заключается в том, что на малом промежутке изменения независимой переменной

интегральная кривая дифференциального уравнения

                              (8)

заменяется отрезком прямой (касательной)

.

Отсюда   и процесс можно повторить для промежутка   и т.д. Число h является здесь шагом таблицы.

Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера 

Рабочая формула для определения значений у по методу Эйлера имеет вид

                               (9)

где

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага, вообще говоря, систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае метод двойного счета – с шагом h и с шагомh/2. Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными. Ошибка метода пропорциональна h2. Существуют различные уточнения метода Эйлера, повышающие его точность так, что ошибка метода становится пропорциональной h3([13]).

21. метод рунге кутта.

Для решения ДУ лин и нелин. Сущность – очень точный метод до 4 знака после ,. Понятие точный и приближенный в решении ДУ.

22. 10,Математическая формулировка задачи отыскивания наименьшего значения функции нескольких переменных с ограничениями в виде равенств и неравенств.

Основные понятия методов нелинейного программирования

В большинстве инженерных задач построение математической модели не удается свести к задаче линейного программирования.

Математические модели в задачах проектирования реальных объектов или технологических процессов должны отражать реальные протекающие в них физические и, как правило, нелинейные процессы. Переменные этих объектов или процессов связанны между собой физическими нелинейными законами, такими, как законы сохранения массы или энергии. Они ограничены предельными диапазонами, обеспечивающими физическую реализуемость данного объекта или процесса. В результате, большинство задач математического программирования, которые встречаются в научно-исследовательских проектах и в задачах проектирования – это задачи нелинейного программирования (НП).

Для решения задачи нелинейного программирования было предложено много методов, которые можно классифицировать по различным признакам.

По количеству локальных критериев в целевой функции методы нелинейного программирования делятся на:

однокритериальные,

многокритериальные.

По длине вектора   методы делятся на:

однопараметрические или одномерные (n=1),

многопараметрические или многомерные (n>1).

По наличию ограничений методы нелинейного программирования делятся на:

без ограничений (безусловная оптимизация),

с ограничениями (условная оптимизация).

По типу информации, используемой в алгоритме поиска экстремума методы делятся на:

методы прямого поиска, т.е. методы, в которых при поиске экстремума целевой функции используются только ее значения;

градиентные методы первого порядка, в которых при поиске экстремума функции используются значения ее первых производных;

градиентные методы второго порядка, в которых при поиске экстремума функции наряду с первыми производными используются и вторые производные.

Ни один метод нелинейного программирования не является универсальным. В каждом конкретном случае необходимо приспосабливать применяемый метод к особенностям решаемой задачи.

23. СВЕДНИЕ УРАВНЕНИЯ К СИСТЕМЕ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА. Сведение уравнения m-го порядка к системе m уравнений первого порядка. Рассмотрим уравнение m-го порядка

f(t, x, xў, ..., x(m–1), x(m)) = 0. (18)

Это уравнение может быть сведено к системе m дифференциальных уравнений первого порядка с помощью замены

y1 = x,

y2 = xў,

...

ym-1 = x(m–2),

ym = x(m–1).

(19)

Формально продифференцировав уравнения (19) и воспользовавшись уравнениями (18) и (19), получим следующую систему уравнений

yў1 = y2,

yў2 = y3,

...

yўm-1 = ym,

f(t, y1, y2, ..., ym, yўm)= 0.

(20)

Покажем, что уравнения (18) и (20) эквивалентны с учетом замены (19). Действительно, пусть x = j(t), y1 = y1(t), ..., ym = ym(t) — решение системы (18) Щ (19). Проделав, уже не формально (дифференцировать теперь можно), описанные при выводе системы (20) действия, получим, что y1 = y1(t), ..., ym = ym(t) — решение системы (20). Импликация (20) Щ (19) Ю (18) доказывается аналогично. Остается заметить, что замена (19) очевидно допустима для уравнения (18) и (20).