1.7. Смесь идеальных газов

Газовой смесью понимается смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси. Парциальное давление – это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объеме и при той же температуре, что и в смеси. Газовая смесь подчиняется закону Дальтона: ║Общее давление смеси газов равно сумме парциальных давлений ║отдельных газов, составляющих смесь.

Р = Р₁ + Р₂ + Р₃ + . . .Р_n = ∑ Р_i , (2.14)

где Р₁ , Р₂ , Р₃ . . .Р_n – парциальные давления. Состав смеси задается объемными, массовыми и мольными долями, которые определяются соответственно по следующим формулам:

r₁ = V₁ / V_см ; r₂ = V₂ / V_см ; … r_n = V_n / V_см , (2.15) g₁ = m₁ / m_см ; g₂ = m₂ / m_см ; … g_n = m_n / m_см , (2.16) =a r₁^′ = ν₁ / ν_см ; r₂^′ = ν₂ / ν_см ; … r_n^′ = ν_n / ν_см , (2.17)=x

где V₁ ; V₂ ; … V_n ; V_см –объемы компонентов и смеси; m₁ ; m₂ ; … m_n ; m_см – массы компонентов и смеси; ν₁ ; ν₂ ; … ν_n ; ν_см – количество вещества (киломолей) компонентов и смеси.

Для идеального газа по закону Дальтона:

r₁ = r₁^′ ; r₂ = r₂^′ ; … r_n = r_n^′ . (2.18)

Так как V₁ +V₂ + … + V_n = V_см и m₁ + m₂ + … + m_n = m_см ,

то r₁ + r₂ + … + r_n = 1 , (2.19) g₁ + g₂ + … + g_n = 1. (2.20)

Связь между объемными и массовыми долями следующее:

g₁ = r₁∙μ₁/μ_см ; g₂ = r₂∙μ₂ /μ_см ; … g_n = r_n∙μ_n /μ_см , (2.21)

где: μ₁ , μ₂ , … μ_n , μ_см – молекулярные массы компонентов и смеси. Молекулярная масса смеси:

μ_см = μ₁ r₁ + r₂ μ₂+ … + r_n μ_n . (2.22)

Газовая постоянная смеси:R_см = g₁ R₁ + g₂ R₂ + … + g_n R_n = = R_μ (g₁/μ₁ + g₂/μ₂+ … + g_n/μ_n ) = = 1 / (r₁/R₁ + r₂/R₂+ … + r_n/R_n) . (2.23)

Удельные массовые теплоемкости смеси:

с_{р см.} = g₁ с_{р 1} + g₂ с_{р 2} + … + g_nс_{р n} . (2.24) с_{v см.} = g₁с_{р 1} + g₂с_{v 2} + … + g_nс_{v n} . (2.25)

Удельные молярные (молекулярные) теплоемкости смеси:

с_{рμ см.} = r₁ с_{рμ 1} + r₂ с_{рμ 2} + … + r_nс_{рμ n} . (2.26) с_vμсм. = r₁с_{vμ 1} + r₂с_{vμ 2} + … + r_nс_{vμ n} . (2.27)

Тема 2. Физические основы горения.

2.1. Свойства газов.

Основное уравнение кинетической теории газов имеет вид:

, (2.1)

где: W_K – суммарная кинетическая энергия поступательного движе-

ния n молекул газа, находящегося в объеме V;

m_i, _i – масса и скорость движения i-той молекулы.

В результате беспорядочного движения и соударений газа происходит изменение скорости и энергий частиц. Возникают явления направленного пе-реноса внутренней энергии, т.е. теплопроводность, и переноса массы частиц, – диффузия с выравниванием того и другого в объеме вещества.

Теплопроводность возникает в веществе при наличии градиента тем-ператур:

, (2.2)

где: dQ – количество теплоты переносимой за время dT через поверхность dS по направлению нормали Х к этой поверхности в сторону убывания температуры;

(dT/dх) – градиент температуры;

k – коэффициент теплопроводности, равный количеству теплоты, перенесенный через единицу поверхности за единицу времени при градиенте dT/dх=1.

Согласно кинетической теории газов:

, Дж/(смсекград) (2.3)

где: υ – средняя скорость теплового движения молекул;

 - средняя длина свободного пробега молекул;

 - плотность газа;

C_V – удельная теплоемкость газа при постоянном объеме.

Диффузией называется процесс установления внутри фаз какой-то сис-темы равномерного распределения концентрации газа.

Фазой называется совокупность всех гомогенных частей системы. В гомогенной системе нет поверхностей раздела фаз (например, газовая фаза, раствор, твердая фаза), т.е. фаза находится в одном агрегатном состоянии. Система, состоящая из двух и более фаз, называется гетерогенной.

В двухкомпонентной системе явление диффузии описывается законом Фика:

, (2.4)

где: dM – масса первого компонента, которая переносится за время d через площадь dS в направлении нормали Х к этой площадке в сторону убывания плотности первого компонента;

d/dx – градиент плотности;

d – коэффициент диффузии.

, см²/сек. (2.5)

Теплоемкостью называется количество тепла, необходимое для повы-шения температуры вещества на один градус:

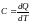, Дж/(гК) (2.6)

Различают C_P – теплоемкость при P=const и C_V – теплоемкость при V=const, которые объединяются соотношением:

, (2.7)

где: R – универсальная газовая постоянная, равная работе, совершае-мой 1 молем идеального газа при изобарном нагреве P=const на 1 градус:

.

Понятия «моль», «R» вытекают из основных законов идеальных газов (идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом).

Кроме закона Бойля-Мариотта это следующие законы:

1. Закон Авогадро: Равные объемы газов при одинаковых температуре и давлении содержат одинаковое число молекул.

Различие в массах веществ определяется разными весами их атомов и молекул. За единицу массы в молекулярной теории принят моль (г-молеку-ла). 1 моль – такая масса химически однородного вещества, которая (в грам-мах) численно равна его молекулярному весу.

Иногда закон Авогадро гласит так: «При одинаковых давлениях и тем-пературах грамм-молекулы различных идеальных газов имеют одинаковые объемы».

Число Авогадро: в 1 моле газа содержится 6,0210²³ молекул. Тогда 1 моль любого газа при 0 ^оС и 101,3 кПа занимает объем 22,414 л.

Другими словами, молекулярный вес – это вес 6,0210²³ молекул газа, выраженный в граммах. Тогда PV=22,4 латм/моль при 0 ⁰С.

Например: атомный вес кислорода – 16. Молекулярный вес 162=32 г. Тогда в 32 г О₂ содержится 6,0210²³ молекул О₂.

Можно рассчитать удельный вес (плотность) газа при нормальных фи-зических условиях:

.

где:  - молекулярный вес газа.

2. Закон Гей-Люссака: при P=const объем массы газа прямо пропорцио-нален его абсолютной температуре:

, (2.8)

где: Т₀=273 К;

V₀ – объем газа при Т₀.

3. Закон Шарля: при V=const давление данной массы газа прямо про-порционально его абсолютной температуре:

, (2.9)

где: P₀ – давление при Т₀=273 К.

4. Уравнение состояния идеального газа для 1 моля газа:

, (2.10)

где: P, V_μ и T – давление, молекулярный объем и абсолютная темпе-

ратура газа.

5.Уравнение Менделеева-Клайперона для произвольной массы газа (М):

, (2.11)

Связь ТГВ с рассмотренными законами и свойствами газов можно показать на следующих примерах.

1. Горение представляет собой комплекс взаимосвязанных физических и химических процессов. Важнейшими из них при горении являются тепло- и массоперенос. Наиболее общим свойством горения является способность возникшего очага (фронта) пламени перемещаться по горючей смеси путем теплопроводности и диффузии активных частиц из зоны горения в свежую смесь. Таким образом, скорость распространения пламени при горении и взрыве зависит от теплопроводности реагирующих веществ. С увеличением теплопроводности скорость горения возрастает.

2. Теплоемкость учитывается в термодинамических расчетах горения и выборе огнетушащих средств. Этот параметр относится как к физике, так и к термохимии, т.к. горение – это химическая реакция. Зависимость теплоемко-сти от температуры веществ выражается уравнением:

C_P =a+bT+cT², (2.12)

где: а, b, c – термодинамические константы.

3. R входит во все уравнения ТГВ.

4. Диффузия объясняет возникновение и протекание так называемого диффузионного горения.

5. На базе основных законов идеальных газов выведены постулаты тео-рии горения и самовоспламенения.

6. Законы идеальных газов являются основой расчетов давления, объе-ма, температуры в процессах горения и взрыва.