2.1.2 Формализация модели

Математическая модель объекта является аналитической, т.е. составляется в форме систем дифференциальных и алгебраических уравнений.

Cистема дифференциальных уравнений электрического равновесия ОЭМП представляет собой четыре уравнения Кирхгофа для четырех обмоток

(2.1) где r₁, r₂ – активные сопротивления соответственно статора и ротора; i_1α,i_1β,i_2d,i_2q – соответственно токи обмоток статора и ротора.

Потокосцепления по осям определяются, как

(2.2)

Индексы при индуктивностях L_i,j обозначают, в какой обмотке (i) и током какой обмотки (j) создается потокосцепление. Уравнения можно переписать:

(2.3) (2.4)

Совместное решение системы уравнений (2.1) невозможно, так как уравнения записаны в различных системах координат. Уравнения (2.1), (2.2) можно переписать в системе координат статора:

(2.5)

где p=d/dt – оператор дифференцирования

L₁, L₂, L_m – соответственно полные индуктивности статора, ротора и взаимная индуктивность

В матричной форме записи:

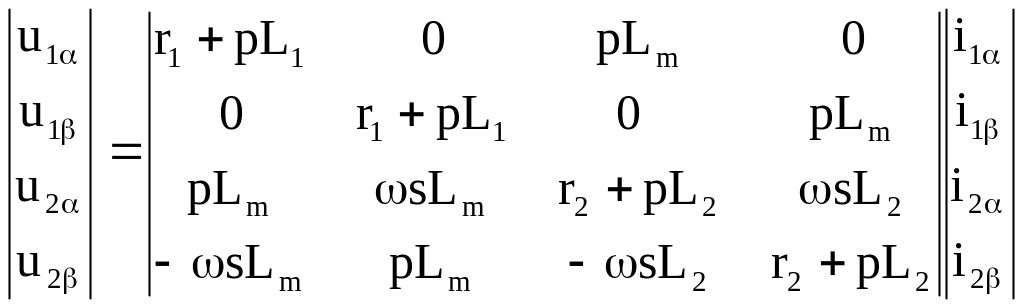(2.6)

Взаимодействие полей статора и ротора ЭМП создает электромагнитный момент

(2.7) Уравнения (2.6), (2.7) совместно с уравнением движения (2.8)

описывают процессы электромеханического преобразования энергии.

6) Программная реализация математической модели

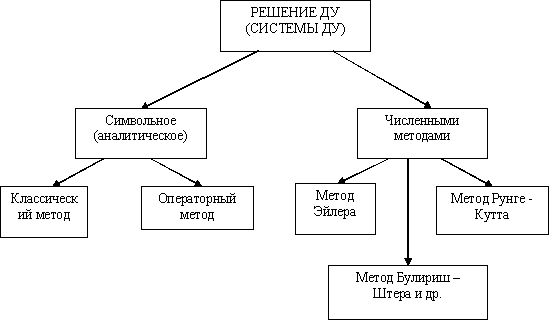
При формализации математической модели необходимо выбрать метод решения дифференциального уравнения (или системы уравнений), описывающих данный динамический процесс. Символьные (аналитические) способы наиболее точны и предпочтительны, но не всегда осуществимы (сложность и громоздкость решения или его невозможность). Значительную помощь в проведении символьных расчетов может оказать использование пакетов символьной математики «Maple» или «Mathematica» Использование современных вычислительных средств значительно повысило точность приближенных численных методов, их быстродействие. Многие математические компьютерные приложения упрощают применение численных методов расчета и делают их универсальными. В случае, когда модель (или подсистему) можно достаточно просто описать и решить аналитическими способами, предпочтение следует отдать последним. Наиболее распространенными в настоящее время пакетами математических прикладных программ для инженерных расчетов являются «Mathcad» и «Matlab».

7) Аналитическое решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя

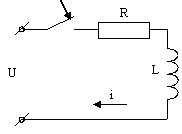
Рассмотрим аналитическое решение ДУ на примере простейшей электрической схемы (рисунок 1)

а) Классический способ

Рассмотрим простейшее звено, описываемое дифференциальным уравнением первого порядка

Примем, что при замыкании ключа установившемуся значению тока i_уст соответствует частное решение дифференциального уравнения

i_уст=U/R

Это решение следует сложить с решением однородного уравнения, описывающего неустановившийся процесс:

имеющим решение ,

где T=L/R – постоянная времени.

Сложим оба решения с условием, что в момент времени t=0 ток, до этого равный нулю, мгновенно измениться не может:

.

Следовательно,k=-U/R, и полное решение

б) Операторный метод

Операторный метод решения ДУ предусматривает замену в уравнениях функций – оригиналов их изображениями в соответствии с преобразованиями Лапласа, решение полученных алгебраических уравнений (где дифференцирование и интегрирование заменяются соответственно умножением и делением) и обратное преобразование полученных результатов.

В обоих случаях, решение даже простейшего уравнения потребует определенных затрат времени. Аналитическое решение уравнений Кирхгофа для ОЭМП затруднено учетом взаимной индуктивности фаз статора и ротора. Совместное же решение уравнений (2.6) – (2.8) в аналитическом виде невозможно из-за нелинейности уравнения момента. Численному решению этой системы ДУ альтернативы нет.

8)-9) Численное решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя. Решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя методом Эйлера

Практически все задачи, относящиеся к анализу динамических систем и к их математическому моделированию, базируются на численных методах решения систем ДУ

Простейшим численным методом решения одиночного дифференциального уравнения вида

является метод Эйлера. Он реализуется следующей рекуррентной формулой:

.

Здесь h— шаг решения. Погрешность этого метода значительна (порядка h), поэтому он на практике почти не применяется.

В документе, показанном на рис. 14.47, дана реализация в приложении «Mathcad» так называемого моди­фицированного метода Эйлера, погрешность которого близка к h² (то есть по­рядка 1% при h =0,1), что нередко уже приемлемо для приближенного решения дифференциальных уравнений первого порядка.

Улучшение точности вычислений при использовании этого метода фактически достигнуто за счет интегрирования методом трапеций вместо метода прямо­угольников, характерного для реализации простого метода Эйлера. В конце рис. 14.47 показано точное решение дифференциального уравнения, взятого для этого примера.

На рис. 14.48 представлена вторая часть данного документа, на которой даны графики точного решения (сплошная линия) и приближенного численного решения модифицированным методом Эйлера. Нетрудно заметить, что точки (ввиду невысокой точности оценки вычислений по графикам) очень плотно укладываются на кривую точного решения.

Однако из таблиц векторов точного и приближенного решения, также представ­ленных на рис. 14.48, заметно расхождение результатов в конце решения уже в третьем знаке после десятичной точки.