Реакторы с различным тепловым режимом

•Для стационарного теплового режима сумма тепла всех взаимодействующих потоков равна нулю:

где Q_то - теплообмен с окружающей средой.

При нестационарном режиме происходит накопление теплоты:

В реакторах с изотермическим режимом температура реаген­тов на входе в реактор и на выходе из него равна

•В реакторах с адиабатическим режимом отсутствует теплообмен с кружающей средой:

В проточном РИС с не изотермическим режимом тепловые потоки

за d  составят

где Ср - средняя теплоемкость;

р - средняя плотность реакционной смеси;

Q₁ - тепловой эффект реакции на 1 моль реагирующего компонента;

dТ_ТО - движущая сила теплообмена;

К_Т -коэффициент теплопередачи;

F - поверхность теплообмена с окружающей средой.

Уравнение теплового баланса при накоплении теплоты в реакторе за

dQ_нак = d(vpCpT) имеет вид

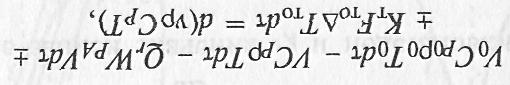
после переноса d в правую часть уравнения:

Кроме этого уравнения математическая модель содержит урав-нение материального баланса

ВЫВОДЫ

1.Сопоставление математических моделей РИС и РИВ

показывает более высокую производительность РИВ

2.Ячеечная модель реактора с неидельной структурой

потоков основана на его дифференцировании на

участки, адекватные идеальному реактору РИС

3.Однопараметрическая диффузионная модель включает

физическое обоснование математического описания процесса

Лекция 6

ПЛАН ЛЕКЦИИ

1.Адиабатический РИС в неизотермическом режиме

2.Тепловая устойчивость химических реакторов

3.Параметрическая чувствительность ректоров

4.Оптимальный температурный режим

Для адиабатического РИС с неизотермическим режимом математическая модель

Решение этой системы уравнений зависит от свойств ФХС, положенной в основу ХТП, т.е. от порядка химического; превращения и знака при энтальпии системы. Однако проводят и некоторое ее упрощение исключением влияния температуры на теплоемкость, плотность и тепловой эффект реакции. Уравнения являются трансцендентными и решаются графическим методом

Реактор РИВ-Н с неизотермическим режимом представляет собой цилиндрическую колонну или горизонтальный канал F = R2. Если линейная скорость W и физические свойства ФХС постоянны, то уравнение теплового баланса следующее:

•Реактор РИВ-Н с неизотермическим режимом представляет собой цилиндрическую колонну или горизонтальный канал

• F = R². Если линейная скорость W и физические свойства ФХС постоянны, то уравнение теплового баланса следующее:

где dF_ТО - поверхность теплообмена (если теплообмен происходит через стенку реактора, то dF _ТО = 2 Rdz);

rA - скорость реакции.

Для стационарного режима после преобразований .

Уравнение теплового баланса решают совместно с уравнениями материального баланса

Тепловая устойчивость химических реакторов

При анализе совместного решения уравнений материального и теплового балансов адиабатического РИС для экзотермических реакций было показано, что возможны случаи, когда система имеет не одно, а несколько решений. Это означает возможность множественности стационарных состояний этой системы.

Устойчивость системы в стационарном состоянии определяется ее реакцией на возмущающие воздействия.

Стационарные состояния системы называется устойчивым, если небольшие кратковременные возмущающие воздействия не могут вывести систему за пределы небольшой области, окружающей исследуемый стационарный режим.

Параметрическая чувствительность по отношению к температуре реакционной смеси на входе в реактор выражается производной dT₂ / dT₁ и показывает, как изменяется температура на выходе из реактора при изменении температуры на входе на 1 градус.

Таким путем можно установить параметрическую чувствительность по температуре. Для этого

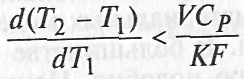
или

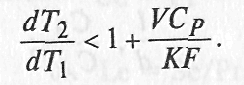
Преобразованиемнеравенства получают

Из теплового баланса:

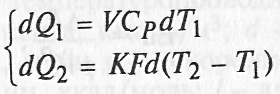
Следует что:

или

Подстановкой в неравенство получают

Оптимальный температурный режим и способы его осуществления в промышленных реакторах

Температурный (тепловой) режим проведения химического процесса, обеспечивающий экономически целесообразную максимальную производительность единицы объема реактора (интенсивность) по целевому продукту, называют оптимальным

Простые необратимые реакции. Уравнение скорости необратимых экзо- и эндотермических реакций можно записать в виде

Из уравнения видно, что принципиальных ограничений повышения температуры с целью увеличения скорости необратимых реакций нет. С ростом степени превращения реагентов скорость реакции падает. Для компенсации этого уменьшения целесообразно увеличивать температуру.

Эндотермическая реакция сопровождается поглощением теплоты. Следовательно, такие реакции невыгодно проводить в адиабатических условиях, так как по мере протекания реакции ее скорость будет падать как из-за увеличения степени превращения, так и из-за уменьшения температуры.

Обратимые химические реакции.

Скорость реакции А R

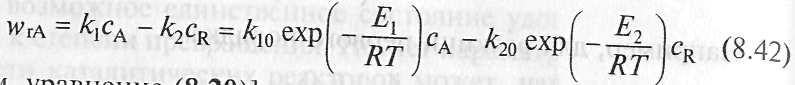
Характер изменения скорости с ростом температуры будет разным для эндо- и экзотермических реакций

При фиксированной степени превращения ход скорость обратимой эндотермической реакции с ростом температуры монотонно увеличивается.

Так как скорость эндотермической реакции — функция нескольких переменных (по меньшей мере, двух — Т и х_А, то для анализа этой функции удобно использовать ее сечение при постоянстве всех переменных, кроме одной.

Существует оптимальная температура Т_т, при которой скорость реакции при заданной степени превращения является максимальной

П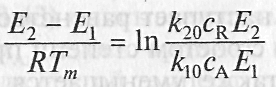 ри Т= Т_М

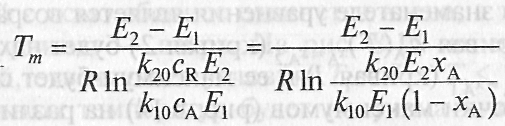и ли

ВЫВОДЫ

1.Устойчивость системы в стационарном состоянии

определяется ее реакцией на возмущающие воздействия

2.Параметрическая тепловая чувствительность показывает

как изменяется температура на выходе из реактора при

изменении температуры на входе на 1 градус

3.Оптимальный температурный режим обеспечивает максимальную

производительность единицы объема реактора по целевому продукту