Модели реакторов с неидеалной структурой потоков
Разработаны две модели учета неидеальности потока, в некоторой степени приближающие расчеты к существующим в реакторах и реакционных агрегатах реальным процессам. Первая из них основана на мысленной замене реального реактора некоторой комбинацией идеальных аппаратов (ячеечная модель), вторая - на введении большего физического обоснования в системе математического описания процесса, в том числе и с помощью математических операторов (однопараметрическая диффузионная модель).
•Ячеечная модель. Реальный аппарат расчленяют на N последовательно соединенных реакторов идеального смешения (ячеек). Сумма всех ячеек равна объему проектируемого реактора. Такой подход вытекает из организации каскада реакторов РИС-Н;
•Каскад при N ~ 1 представляет собой единичный реактор идеального смешения, а при N = и бесконечно малых объемах секций dV -реактор идеального вытеснения.
•Как правило, при N < 10 можно удовлетворительно описать реальный реакционный узел в реакционном агрегате. Число ячеек, представляющее реальный реактор, - единственный параметр ячеечной модели. Зная необходимое число N, рассчитывают каждую ячейку идеального смешения.
•Однопараметрическая диффузионная модель.
•В диффузионной модели учитывают перемешивание реакционной смеси в осевом направлении, которое происходит благодаря различным видам диффузии. Изменение концентрации реакционного компонента в связи с появлением турбулентной или тейлоровской диффузии описывают как и при молекулярной диффузии, но с применением коэффициентов Dтурб. или Dтейл.
•В расчеты по этой модели вводят некоторые условия по аналогии с системой аксиом:
•- по сечению реактора, перпендикулярного оси аппарата, состав не изменяется, изменения происходят только вдоль оси аппарата;
•- в аппарате отсутствуют застойные зоны и байпасные потоки
•При составлении уравнения материального баланса принимают модель идеального вытеснения по веществу А,
•элементарный объем реактора
•dVp = FdZ
• промежуток времени d.
• В соответствии с принятыми допущениями концентрация компонента , зависит от двух переменных:
• при нестационарном режиме СА = CA(Z, )
• при стационарном только от координаты CA(Z).
•Реагент А поступает в dV за d путем конвективного и диффузионного переноса:
Диффузионный перенос вещества А выражают в структуре уравнения Фика.
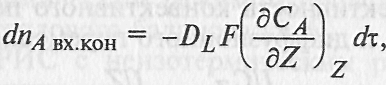Коэффициент
диффузии DL
объединяет
вcе
виды диффузии при продольном перемешивании:
Г
де
- градиент концентрации
в сечении Z
по направлению переноса.
•При изменении координаты возможно приращение концентрации на
(CA/ Z) dZ и увеличение градиента концентрации на
( 2 CA / Z2) dZ
В результате этого
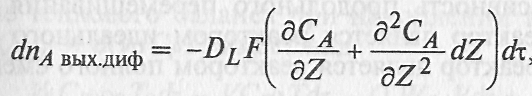
где п ~ удельный выход каждого вида изменения концентрации А
V~ объем реактора; Vр - объем реакционной смеси.
Преобразовав и соединив все виды п в единое уравнение Получают уравнение, описывающее нестационарный процесс ] Реальном реакторе при наличии продольного перемешивания:
Преобразовав и соединив все виды n в единое уравнение получают уравнение, описывающее нестационарный процесс в реальном реакторе при наличии продольного перемешивания:
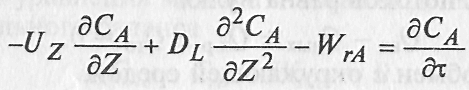
где Uz= - F- линейная скорость потока в реакторе по его оси
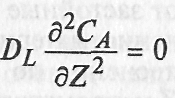
При отсутствии осевого перемешивания
У
равнение
принимает вид:
где dl ~ dZ ; W= vF, м/с.
Воспользовавшись методами подобия, получают критерий, отражающий эффективность конвективного переноса вдоль оси (высоты) аппарата и диффузионного перемешивания:
где U- линейная скорость; Z- линейный размер, равный L.
О
тсюда
критерий Боденштейна (Пекле) равен
В том случае, когда в реакторе большие линейные скорости или низкие значения продольной диффузии, величина Во большая и интенсивность продольного перемешивания низкая,
т.е. Во -» и реактор является реактором идеального вытеснения.
При Во -» 0 реактор является реактором полного смешения.