2.5 Выбор закона регулирования и проверка системы на устойчивость

2.5.1 Определение динамических характеристик объекта управления

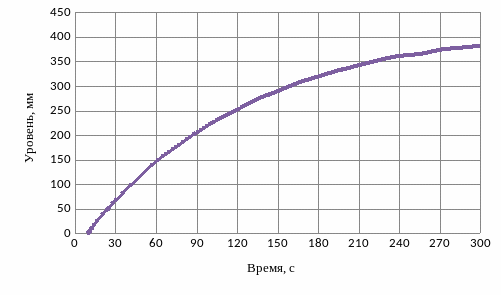
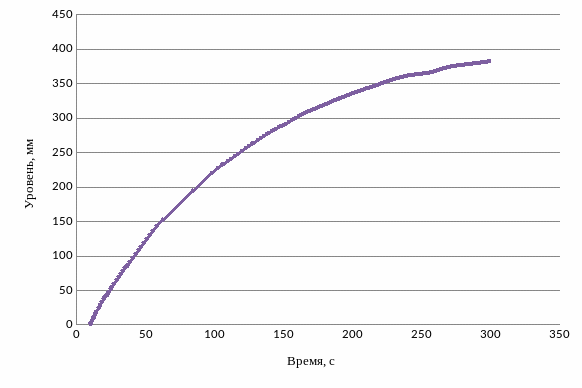
Для определения динамических характеристик объекта управления задается переходный процесс в виде графика, изображенного на рисунке 2.13. Произведя оцифровку точек на графике, заполняется таблица исходных значений и по ним строится переходный процесс (рисунок 2.14):

Используя метод наименьших квадратов, составляется уравнение касательной (2.7):

y = a + bx, (2.7)

где a, b – коэффициенты;

x – входная величина;

y – выходная величина.

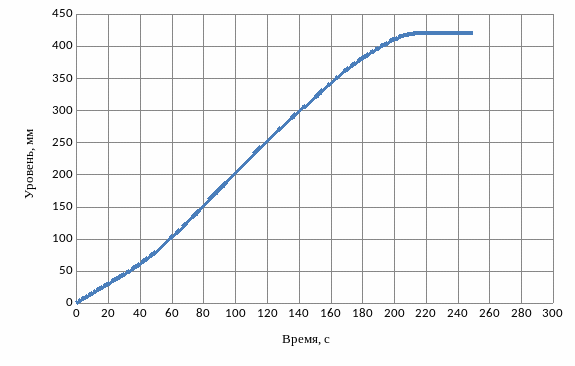
Рисунок 2.13 – Переходный процесс

Для определения коэффициентов a и b составляется система уравнений 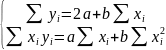(2.8):

(2.8)

где x_i – входной сигнал в точке i;

y_i –выходной сигнал в точке i.

Данные для нахождения уравнения касательной указаны в таблице 2.8.

Таблица 2.8 – Данные для нахождения уравнения касательной

Точки характеристики	xi	yi	xi2	xiyi
1	80	150	6400	12000
2	140	300	19600	42000
Ʃ	220	450	26000	54000

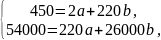
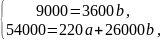
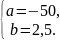
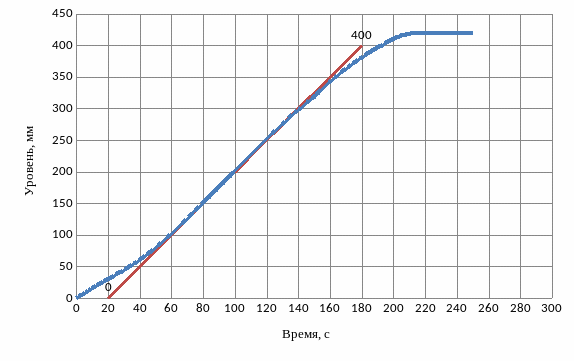
1 – переходный процесс; 2 – касательная.

Рисунок 2.14 – График для определения динамических характеристик объекта

По рисунку 2.14 определяются характеристики объекта:

– по уравнению (2.9) определяется время запаздывания τ_з:

y = -50+2,5x, (2.9)

где x – входная величина;

y – выходная величина.

y = 0,

0 = -50+2,5x,

x = τ_з = 20 с;

– коэффициент передачи объекта k_об определяется по формуле (2.10):

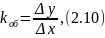
где ∆x – изменение входной величины;

∆y – изменение выходной величины.

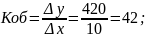
– используя уравнение (2.9) определяется постоянная времени Т_об по формуле (2.11):

y = 420,

-50+2,5x,

x=148.

Т_об = x- τ_з, (2.11)

где x = 148;

τ_з – время запаздывания.

Т_об=148-20=128 с;

– время переходного процесса t_пер определяется в соответствии с формулой (2.12):

t_пер = 2∙T_об, (2.12)

где T_об – постоянная времени.

t_пер = 2∙128 = 256 с.

2.5.2 Аппроксимация моделью первого порядка

Исходные данные об объекте задаются в виде графика его переходной функции. Предполагается, что у переходной функции модели первого порядка отсутствуют колебания, т.е. она имеет качественный вид.

Передаточная функция H_м(p) имеет вид, соответствующий формуле (2.13):

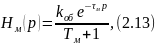
где k_об – коэффициент передачи объекта;

τ_м – расчетное значение времени запаздывания;

p – символ дифференцирования;

Т_м – расчетное значение постоянной времени.

Ей соответствует переходная функция в виде формулы (2.14):

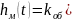
где h_м(t) – координата точки перегиба;

t – время;

k_об – коэффициент передачи объекта;

τ_м – расчетное значение времени запаздывания;

Т_м – расчетное значение постоянной времени.

По формуле (2.15) рассчитывается коэффициент b:

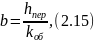
где h_пер = h_м(t_пер) – координата точки перегиба;

k_об – коэффициент передачи объекта.

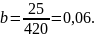
По формулам (2.16), (2.17) определяются Т_м и τ_м:

Т_м = Т_об∙(1-b), (2.16)

τ_м = t_пер.+Т_м∙ln(1-b), (2.17)

где Т_м – расчетное значение постоянной времени;

T_об – постоянная времени;

b – коэффициент;

τ_м – расчетное значение времени запаздывания;

t_пер – координата точки перегиба.

Т_м = 128∙(1-0,06) = 120,32 с,

τ_м = 16,25+120,32∙ln(1-0,06) = 8,81 с.

Строим переходную функцию модели (рисунок 2.15), используя формулу (2.14).

1 – переходный процесс; 2 – аппроксимация первого порядка.

Рисунок 2.15 – Аппроксимация моделью первого порядка

2.5.3 Аппроксимация моделью второго порядка

Аппроксимация моделью второго порядка осуществляется следующими способами:

– аппроксимация двумя инерционными звеньями первого порядка с разными постоянными времени;

– аппроксимация двумя инерционными звеньями первого порядка с одинаковыми постоянными времени.

Для аппроксимации двумя инерционными звеньями первого порядка с разными постоянными времени можно выбрать передаточную функцию второго порядка с запаздыванием τ_ч и различными постоянными времени.

Передаточная функция H_м(p) имеет вид, соответствующий формуле (2.18):

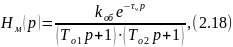
где k_об – коэффициент передачи объекта;

τ_ч – чистое запаздывание;

p – символ дифференцирования;

Т_о1, Т_о2 – расчетные значения постоянной времени.

В большинстве случаев модель обеспечивает достаточную точность для практических расчетов, если принять Т_о1 /Т_о2 = 0,5 при этом постоянные времени Т_о1 и Т_о2 определяются следующим образом по ординате h(t₂) в соответствии сформулами (2.19), (2.20), (2.21):

h(t₂) = 0,63∙k_об, (2.19)

где k_об – коэффициент передачи объекта.

T_o2 = 0,64∙t₂ , (2.20)

T_o1 = 0,5∙T_o2, (2.21)

где t₂ – момент времени, определяемый по ординате h(t₂) экспериментальной переходной характеристики, t₂=126.

h(t₂) = 0,63∙420 = 264,6,

T_o2 = 0,64∙126 = 80,64 с,

T_o1 = 0,5∙80,64 = 40,32 с.

Полученный переходный процесс изображён на рисунке 2.16.

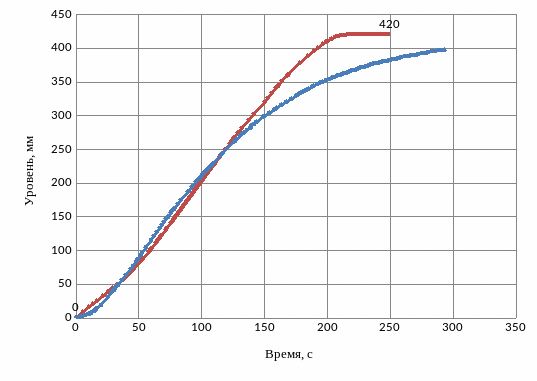
1 – переходный процесс; 2 - аппроксимация двумя инерционными звеньями первого порядка с разными постоянными времени.

Рисунок 2.16 – Аппроксимация двумя инерционными звеньями первого порядка с разными постоянными времени

Модель второго порядка с одинаковыми постоянными времени и запаздыванием имеет вид, соответствующий формуле (2.22):

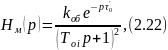
где H_м(p) – передаточная функция;

k_об – коэффициент передачи объекта;

τ’_о – чистое запаздывание, τ’_о = τ_ч;

p – символ дифференцирования;

Т_оi – расчётное значение постоянной времени.

Постоянная времени Т_оi рассчитывается по формуле (2.23):

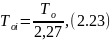
где Т_о – постоянная времени.

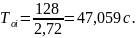
Используя формулу (2.24), рассчитывается чистое запаздывание τ’_о:

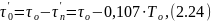
где τ_о – время запаздывания;

Т_о – постоянная времени.

.

Параметры данной модели однозначно выражаются через параметры Т_о и τ_о экспериментальной переходной характеристики (рисунок 2.17).

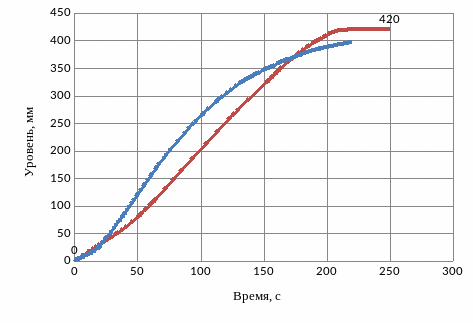
1 – переходный процесс; 2 – аппроксимация двумя инерционными звеньями первого порядка с одинаковыми постоянными времени.

Рисунок 2.17 – Аппроксимация двумя инерционными звеньями первого порядка с одинаковыми постоянными времени

2.5.4 Определение оптимальной передаточной функции

Для определения оптимальной передаточной функции критерием выбора является квадратичный интегральный критерий качества, характеризующий суммарную площадь, ограниченную кривой переходного процесса.

Графики, необходимые для определения оптимальной передаточной функции, представлены на рисунке 2.18.

Интегральная квадратичная ошибка 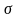вычисляется по формуле (2.25):

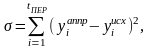(2.25)

где 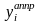– выходная величина аппроксимации;

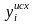– выходная величина переходного процесса.

Данные для вычисления квадратичной ошибки приведены в таблице 2.9.

1 – переходный процесс; 2 – аппроксимация первого порядка; 3 – аппроксимация с двумя инерционными звеньями первого порядка с разными постоянными времени; 4 – аппроксимация двумя инерционными звеньями первого порядка с одинаковыми постоянными времени.

Рисунок 2.18 – Графики для определения оптимальной передаточной функции

Таблица 2.9 – Определение интегральной квадратичной ошибки для различных моделей аппроксимации

Время	Переходные функции объектов и моделей				Вычисление ошибки
	Исходная	1 пор.	2п.разл.Т	2п.один.Т		1 пор.	2п.разл.Т	2п.один.Т
0	0	0	0	0		0	0	0
15	21	20	11	17		1	100	16
30	43	69	40	55		676	9	144
45	70	110	75	103		1600	25	1089
60	102	148	114	151		2116	114	2401
75	140	176	153	200		1296	169	3600
90	178	206	190	239		784	144	3721
105	213	231	220	272		324	49	3481
120	252	251	250	302		1	4	2500

Продолжение таблицы 2.9

Время	Переходные функции объектов и моделей				Вычисление ошибки
	Исходная	1 пор.	2п.разл.Т	2п.один.Т		1 пор.		2п.разл.Т		2п.один.Т
135	286	272	278	328		196		64		1764
150	320	290	300	348		1		400		784
165	353	308	319	360		2025		1156		49
180	380	320	334	373		3600		2116		49
195	402	330	350	385		5184		2704		289
210	419	341	360	391		6084		3481		784
225	420	351	370	399		4761		2500		441
240	420	361	378	402		3481		1764		324
255	420	369	382	409		2601		1444		121
270	420	374	390	411		2116		900		81
285	420	378	393	418		1764		729		4
Ошибка:					38611		17872		21642

Вывод: для дальнейших расчетов выбираем аппроксимацию моделью второго порядка с разными постоянными времени, так как она имеет наименьшую квадратич