2.4 Расчёт статической характеристики методом наименьших квадратов

Метод наименьших квадратов необходимо использовать для того, чтобы получить математическое описание статической характеристики оптимизируемого процесса. Под математическим описанием понимается уравнение статической характеристики, полученной экспериментальным путем. Под оптимизацией понимается нахождение параметров системы, которые являются наилучшими для ее функционирования.

МНЛЗ как объект автоматизации имеет статическую характеристику уровня металла в кристаллизаторе (рисунок 2.11).

С помощью данного метода составляется полином третьей степени, представленный в виде формулы (2.1).

Рисунок 2.11 – Статическая характеристика

у = a+bх+cх²+dx³, (2.1)

где a, b, c, d – коэффициенты;

x – входная величина;

y – выходная величина.

Составляется система уравнений (2.2):

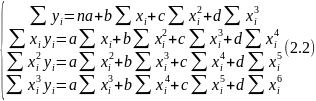
где a, b, c, d – коэффициенты;

n – количество точек;

x – входная величина;

y – выходная величина.

В таблице 2.7 представлены данные для составления системы уравнений (2.2).

Таблица 2.7 – Данные для составления системы уравнений

Точки характеристики	x	y	x2	x3	x4	x5
1	0	5	0	0	0	0
2	20	18	400	8000	160000	3200000
3	50	51	2500	125000	6250000	3,13E+08
4	80	100	6400	512000	40960000	3,28E+09
5	100	140	10000	1000000	1E+08	1E+10
6	120	195	14400	1728000	2,07E+08	2,49E+10
7	140	250	19600	2744000	3,84E+08	5,38E+10
8	150	290	22500	3375000	5,06E+08	7,59E+10
9	160	325	25600	4096000	6,55E+08	1,05E+11
10	180	400	32400	5832000	1,05E+09	1,89E+11
Ʃ	1000	1774	133800	19420000	2,95E+09	4,62E+11

Продолжение таблицы 2.7

Точки характеристики	x6	xy	x2y	x3y
1	0	0	0	0
2	64000000	360	7200	144000
3	1,56E+10	2550	127500	6375000
4	2,62E+11	8000	640000	51200000
5	1E+12	14000	1400000	1,4E+08
6	2,99E+12	23400	2808000	3,37E+08
7	7,53E+12	35000	4900000	6,86E+08
8	1,14E+13	43500	6525000	9,79E+08
9	1,68E+13	52000	8320000	1,33E+09
10	3,4E+13	72000	12960000	2,33E+09
Ʃ	7,4E+13	250810	37687700	5,86E+09

Используя данные таблицы 2.7, определяются коэффициенты a, b, c, d по формулам (2.3), (2.4), (2.5), (2.6):

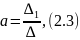
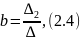
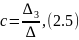
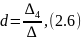
где ∆, ∆₁, ∆₂, ∆₃, ∆₄ – определители.

2,70254E+25,

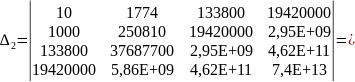2,31838E+24,

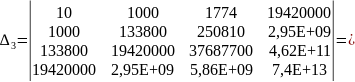4,29E+22,

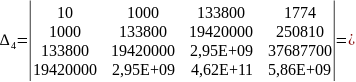3,50733E+19.

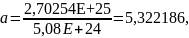
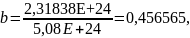
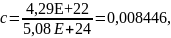
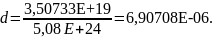
Подставив полученные коэффициенты в полином, указанный в формуле (2.1), получается следующее уравнение:

y = 5,322186 + 0,456565x – 0,008446x² + 6,90708Е–0,6x³.

По полученному уравнению строится экспериментальная статическая характеристика (рисунок 2.12).

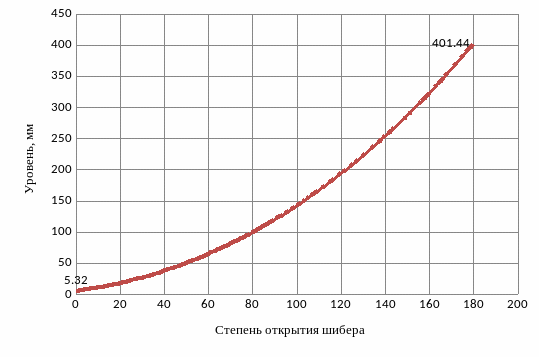
1 – расчётная характеристика; 2 – экспериментальная характеристика.

Рисунок 2.12 – Сравнительный анализ расчетной и экспериментальной характеристик