14. Comparison test 1,2,3.

Comparison test 1.

∞ ∞

Let ∑ an and ∑ Bn be series with nonnegative terms and suppose that an ≤ Bn(4)

n=1 n=1

1. If the “bigger” series ∑ Bn converges, then the “smaller” series ∑an also converges.

2. If the “smaller” series ∑an diverges, then the “bigger” series ∑Bn also diverges.

Proof: (a) if An= ak+ak+1..an and Bn=bk+bk+1..bn, n ≥ k, then the from (4) An ≤Bn(5)

If ∑Bn  ,then {Bn} is bounded above and (5) implies that {An} is also; therefore ∑an.

On the other hand, if ∑an diverges, then the sequence {An} is unbounded above and (5) implies that {Bn} also; therefore ∑Bn diverges.

Comp. test 2

Suppose that an≥ and Bn>0 and lim an/Bn =L,where L.>0. Then ∑an and ∑ bn converges or diverges together.

Comp. test 3

∞

∑ 1/n^p,  if p>1

n=1 diverges if p≤1

15. The d’alemberts test. The raabe’s test. The gauss’s test.

The D’alemberts test

Let ∑an be a series with positive terms and suppose that lim=An+1/An=p

n->∞

1. If p<1, the series 

2. If p >1, the series diverges

3. If p=1, the series may converge and diverge, so that another test must be tried.

Proof: __ __

Suppose that an>0 for n≥k. Then ∑an if lim An+1/an>1 because if lim An+1/an such that

n->∞ n->∞

o<r<1 and An+1/an< r^(n+1)/ r^n.

Since ∑r^n / we use comp.test 1 and the series ∑an . If lim An+1/an>1 there is a number r

---

Such that r>1 and An+1/an>r for n sufficiently large. This can be rewritten as An+1/an > r^(n+1)/r^n. since ∑r^n diverges. Comp test 1 implies that ∑ bn diverges.

Then lim An+1/an < 1, ∑an 

limAn+1/an>1, ∑an diverges.

THE RAABE’S TEST

Suppose that an>0 for large n.

Let lim n( an/An+1 – 1)= p , if p>1, the series 

n->∞ if p<1 , diverges

if p=1, ∑an-?

THE GAUSS’S TEST.

Suppose that an>0, for any n€N

Let an/An+1= ϒ(альфа)+ µ/n +0(c 2мя точками сверху) (1/n)

Then if ϒ>1 => ∑an 

If ϒ<1 => ∑an diverges

If ϒ=1

µ=1 => ∑ an 

if ϒ=1, µ<1 => ∑ an diverges.

16. Cauchy’s root test. Absolute and conditional convergence. Leibnitz’s test. Derichlet’s test. Abel’s test.

Cauchy’s root test.

∞

Let ∑ be a series with positive terms and suppose that lim ak под корнем в степени к= L

n=1 k∞

1. If L<1, the series 

2. If L>1, the series diverges

3. If l=1, may converges or diverges, so that another test must be tried.

Absolute and conditional convergence.

∞

A series ∑ ak= a1+a2+…+ak+… is said to convergence absolutely, if the series of absolute

k=1 ∞

values ∑ |ak|= |a1|+|a2|+…+|ak|+… converges too.

n=1

If the series that converges, but diverges absolutely is said to converges conditionally.

Leibnitz’s test. ∞

∑ (-1)^n an (1)  if

n=1

1. (1) is alternating series

2. An ↓ (monotonically decreasing)

3. Lim an=0

n->1

Derichlet’s test.

∞

∑ an bn  if

n=1 ∞

1. | ∑ an| ≤ k there is k>0, partial sum is bounded

n=1

∞

2. {bn} ↓

N=1

Abel’s test.

∞

∑ an bn  if

n=1

∞

1. ∑ an 

n=1

∞

2. {bn} monotonically ↓↑

n=1

3. |bn| ≤ c , there is c>0

19.The canonical decomposition of LCM (theorem 26 page 38)

Each integer a 0 has only a finite set of divisors.

Proof. Let d/a , then a = dq. Since a = 0, and hence an integer 1, .

There is only a finite set of integers d such that .

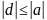20.Prove  [a₁,…,a_n-1,a_n]=[[a₁,…,a_n-1],a_n]. (theorem 33)

That is, the least common multiple of n numbers (n ) can be found by finding the first least common multiple of n – 1 numbers, and then taking the smallest oschee multiple of the number of the thus obtained m’= 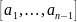and the last number .

Proof: Let 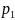, … , - prime numbers dividing at least one of the numbers , … , .

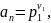… , … , = … , , … , , where integer.

max( )= max (max ( ), )

. . . . . . . . . . . .. . . . . . . . . . . . . . . .. . .. .. . .. .. . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

max( )= max (max ( ), )

( , … , )= … , this proves our theorem.

21.Prove  ab=[a,b] (a,b).(theorem 34)

Let a intger, (a,b)=d and , then dm=ab , i.e. the product of the greatest common divisor and least common multiple of two positive numbers is equal to their product.

Proof: Let … , , 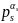… , integer); then:

d= … , ,

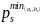m= … ,

,

. . . . . . . . . . . . . . . . . . . . . . . .

,

So that dm=ab.

22.Euchleadean’s Algorithm.(page 43)

Finding the greatest common divisor of the formula are possible if previously found to canonical decomposition numbers under consideration. To find the greatest common divisor of two numbers there Euclidean algorithm.

If b/a and b 2)b/a and b/b 3) if and 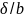, in particular . Since for b executed all conditions (1) defining greatest common divider a and b, (a.b)=b

23.Prove:  a=bc+d  implies  (a,b)=(b,d).(theorem 36)

If a=bc+d , so (a,b)=(b,d).

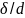Proof: (a,b)=r ;then: 1) r ; 2) of r/a , d/b and d= a-bq follow that r/d; 3) if , , so ; common divider a and b, and, therefore .

Such, all conditions defining r as the greatest common divisor b and d, executed: (a,b)=r=(b,d).

24.Prove:  a=bc+d  implies  (a,b)=(b,d).(theorem 36)

If a=bc+d , so (a,b)=(b,d).

Proof: (a,b)=r ;then: 1) r ; 2) of r/a , d/b and d= a-bq follow that r/d; 3) if , , so ; common divider a and b, and, therefore .

Such, all conditions defining r as the greatest common divisor b and d, executed: (a,b)=r=(b,d).

25.Prove:  (a₁,b)=1,…, (a_n,b)=1 implies  (a₁…a_n.,b)=1.(theorem 42)

If (a₁,b)=1,…, (a_n,b)=1, then (a_1,…a_n.,b)=1, i.e product of numbers each of which is coprime with the same number, also coprime with the number.

Proof: Consider three cases:

1)b=0. Of the condition ( ,0)=1 get , that 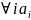=±1, and then (a_1,…a_n.,b)=1

=±1. In this case (a₁…a_n., ±1)=1 for integer a_1,…,a_n.

, ±1. Consider in this case the canonical decomposition =± … 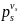. Since (a₁,b)=1,…, (a_n,b)=1, Multipliers 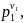… , according to theorem 38 not included in any of the canonical decomposition of numbers a₁…a_n, Therefore not included in any of the canonical decomposition of their product a₁…a_n, such that (a₁…a_n.,b)=1.

26.Prove:  (a,b)=1  implies for any positive  m  and  n  with  (a^m,bⁿ)=1.(theorem 43)

If (a,b)=1  implies for any positive  m  and  n  with  (a^m,bⁿ)=1

1. If for any two positive integers m and n values (a^m,bⁿ)=1, then (a,b )=1

Proof: 1) Of (a,b)=1 for a1=…=am=a (m ) we get (a^m,b)=1 , of this such that for n we get (a^m,bⁿ)=1. If at least one of the numbers n,m=0 this is obvious.

2. If (a^m,bⁿ)=1, n , m and (a,b)=d , of d/a, d/b we successively obtain: d/ a^m. d/ bⁿ ; d/ (a^m,bⁿ ) , d/1 d=1.