8 Дәріс. Ұңғылардың интерференциясы - қабатта бірнеше ұңғылардың өзара әсерлесу кезіндегі сұйықтық фильтрациясын моделдеу
Ұңғы интерференциясы (өзара әсерлесу) құбылысы кезінде, ұңғылардың бір тобының жұмыс тәртібі өзгергенде немесе іске қосу, токтану әсерінен, сол қабатты пайдаланып жатқан басқа бір ұңғылар тобының түптік қысымы мен шығымының өзгеруі жүріп жатады. Қайта іске қосылған ұңғылар жұмыс істеп тұрған ұңғылармен өзара әрекеттеседі.
Ұңғылардың осылайша өзара әрекеттесуі мен өзара әсерлесу құбылысы интерференция деп атайды.
Сұйықтықтың жұтып алатын (бөлетін) жазықтықтағы нүктесі – нүктелік ағын (қайнар көзі) деп атайық.
Ағынды (қайнар көзді) өндіруші (айдаушы) ұңғының центрі деп қарастыруға болады.
Нүктелік ағынның Ф патенциялының енгізіп, оны мына формула арқылы анықтауға болады:
(1)
мұндағы;
q=Q/h - қабат қалындығының бірлігіне келетін ұңғы-ағынның шығымы ;
r - потенциал анықталатын ағыннан қабат нүктесіне дейінгі қашықтық;
С – тұрақты сан;
(1) формуладағы нүктелік қайнар көзі үшін, q шығымы теріс деп есептеледі.
Бірнеше ағын көздері қабатқа бірдей әсер етсе, онда әрбір қайнарға бөлек патенциал Ф (1) формуламен анықталады.
Ол (2) формулада көрсетілген. Бүкіл қайнар мен ағынды сипаттайтын патенциал, бір-бірінен тәуелсіз патенциал мәндерінің қосындысы арқылы есептеледі,
яғни
немесе
(2)
мұндағы
.
1. Коректену өнбойынан (ҚӨ) алшақтатылған қабаттағы ұңғылар тобына сұйықтықын ағыны (1-сурет).
Қалыңдығы
h көлденнен қабаттағы , А
,
А
,
… А
ұңғылар тобы орналасқан, ал олардың
радиусы r
,
олар әртүрлі түптік потенциалдармен
Фсі
жұмыс істеп тұрады, мұндағы i = 1,2,…n.
i – ші
және j – ші ұңғылар центірінін ара
қашықтығы берілген, ол мынаған тең
=
.
Қоректену өнбойы ұңғыдан алыс қашықтықта
орналасқандықтан, жуықтап алғанда,
барлық ұңғылардан бастап, ҚӨ - ның барлық
нүктелеріне дейінгі қашықтық, бәрібір
rк
-
ға теңгеріледі. ҚӨ -ндағы Фк
патенциалы
берілген деп есептеледі. М қабатының
кез-келген нүктесіндегі патенциал (2)
формула арқылы анықталады.
А2
Фк
r13
А1,
Ф1
А3 Ai ,Фi КП
r3n Аn rk
Фк
1-сурет. Көректену нұсқасы қашықтықталған қабаттағы ұңғылар тобындағы сұйықтықтың ағыны (КН) .
Ал
i – ші ұңғы түбінің потенциалы
- мынаған тең:
(3)
i = 1,2, … n.
(3) жүйесі n теңдеулерден тұрады және құрамында (n+1) белгісіздері (n – ұңғы шығымы және интегралдық тұрақтысы ) болады.
КӨ–на М нүктесін орналастырғаннан кейін, біз қосымша теңдеуді аламыз.
(4)
(4) теңдіктен (3) теңдікті санды түрде шегере отырып, тұрақты саннан С-тен құтыламыз және n теңдеуден тұратын мына жүйені аламыз.
Бұны
шеше отырып, ұңғы шығымын q
-ді
есептеуге жеңіл жол аламыз, бірақ бұл
жерде өнбой
және түптік
-
потенциалы берілуі керек.
2. Түзу сызықты қоректену өнбойы бар қабаттағы ұңғыға сұйықтыңтың ағыны.
Түзу сызықты КӨ бар жартылай шексіз қабатта потенциал Фк – ға тең, жалғыз өндіруші ұңғының түбіндегі потенциалы Фс тең болады.
q – ді табу керек.
Бұл есепті шешу үшін ағын ұңғының айналы бейнесі КӨ-на қатысты алымы, ұңғы шығымын теріс (минус) таңбамен аламыз.
М қабаттағы кез келген нүктенің потенциалы мынаған тең:
(5)
rк радиусты ұңғы қабырғасына және КӨ - н рет – ретімен М нүктесін орналастырсақ?
Аламыз
(6)
мұндағы a – ұңғы бастауы мен КӨ арасындағы ең жақын ара қашықтық.
3. Дөңгелек қабатта эксцентрлі орналастырылған ұңғыға келетін сұйықтың ағыны.
rс радиусты дөңгелек ҚӨ бар, тұрақты қалыңдығы h – қа тең жазық қабатта Фк тұрақты патенциялы қалыптасқан. Дөңгелек центрінен а қашықтыққа, Фс тұрақты патенциалды А1 ағын –ұңғысы раноласқан.
ҚӨ -на қатысты А2 фиктивті ұңғы – қайнар көзі арқылы А1 ағын ұңғысын келтірейік.
Қабаттағы М нүктесінің потенциалын (5) формула бойынша анықтаймыз. А1 және қорек өңбойы ұңғымасының қабырғасына М нүктесін орналастыра отырып фс және фк потенциалдарын анықтаймыз. Сонан соң q – ді табамыз.
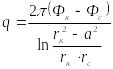(7)
Негізгі әдебиеттер: 1[ 52-96 ]
Қосымша әдебиеттер: 3[ 125-155 ], 5 [16-20].
Бақылау сұрақтары:
Ұңғы интерференциясы (өзара әсерлесу) құбылысы.
Ағынның қайнар көзі және бөлінуі.
Түзу сызықты қоректену өнбойы бар қабаттағы ұңғыма шығымы.
Дөңгелек қабатта эксцентрлі орналастырылған ұңғыма шығымы.