Ағынның үздіксіздік теңдеуі

Деформацияланатын кеуекті ортадағы біртекті сығылатын флюид үшін фильтрациялық ағынның үздіксіздік теңдеуі, кеуекті ортадағы элементарлы көлемдегі масса балансы теңдеуімен түсіндіріледі.

Математикалық түрде ол былай өрнектеледі:

x, y, z координат осьтеріне dx, dy, dz қабырғалары параллель болатын тікбұрышты параллелипипедті қарастырайық.

Уақыт бірлігінде х осі бағытымен параллепипедке dy·dz ּмасса енеді; ол қарама-қарсы жақтан

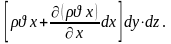
масса түрінде шығып жатыр.

dt бірлік уақыт ішінде x осінің бағытында кіріп - шығып жатқан массалар арасында флюид массаның өзгерісі мынаған тең:

-

Сол сияқты y және z осьтеріне параллель бағыттар үшін:

- -

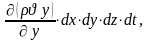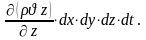
dt уақыт ішінде бүкіл көлемі ішінде массаның жалпы өзгерісі келесідей:

(1)

Бір жағынан қарастылып отырған элементтің флюидінің массасы (pm)ּdxּdyּdz тең.

Массасының dt уақыт ішінде өзгерісі мынаған тең:

(2)

1. мен (2) теңестіріп, мынаны аламыз:

(3)

Дарси заңының дифференциалды түрі

Дарсидің сызықтық заңы

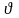= (4)

қабаттағы қиманың тұрақты ауданы үшін шығарылған. қиманың айнымалы ауданында ток түтігі үшін түтік ұзындығы dS бойынша Дарси заңы дифференциалды түрде жазылады.

Егер xy жазықтықтығын қабат жазықтығымен біріктіп, ал z координаттық осін перпендикуляр бағыттасақ, онда Дарси заңын былай жазуға болады:

x = - k/µ∙ p/ x, y = - k/µ∙ p/ y, z= - k/µ∙ p/ z (5)

Кеуекті орта мен флюидтердің күй теңдеуі

Дарси заңының дифференциалдық түрі мен ағының үздіксіздік теңдеуінде тығыздық ρ, кеуектілік коэффициенті m, өткізгіштік коэффициенті k болады.

Изотермиялық үрдісте біртекті флюдтің тығыздығы қысымнан тәуелділігі күй теңдеуін сипаттайды.

1. Тамшылы сұйықтықтың қалыптасқан фильтрациясының тығыздығы қысымға тәуелді емес деп қарастыруға болады, яғни сұйықтықты сығылмайды деп аламыз.

Онда

ρ = const. (6)

2. Сығылатын сұйықтықтар үшін тығыздық пен қысымның өзара қатынасын сұйықтың сығылу βж коэффициентін анықтайтын теңдеу арқылы аламыз:

(7)

бұндағы Vж –сұйықтықтың алғашқы көлемі

Егер қарастырылып отырған сұйық көлемінің массасын М деп алсақ, онда

Vж=М/ρ және =

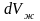болады және (7) теңдік мына түрге келеді:

Осыны интегралдап мынаны аламыз:

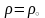
(8)

немесе аз қысымда

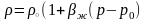₍₉₎

3. Егер газды кенорындардағы қабат қысымы үлкен болмаса (6-9 МПа дейін) және депрессия 1 МПа дейін болса, онда табиғи газды идеалды деп санаймыз.

Идеалды газ күйінің теңдеуі болып, Клайперон–Менделеев теңдеуі қарастырылады.

бұдағы R- газ тұрақтысы

Егер 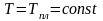болып , ал 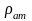– атмосфералық қысым кезіндегі газ тығыздығы болса, онда идеалды газ күйінің теңдеуі мына түрге ие болады:

(10)

Үлкен депрессиямен (15-30 МПа) пайдаланылатын және қабат қысымы жоғары (40-60 МПа дейін) газды кенорындар үшін, газдың күй теңдеуі мынадай болады.

(11)

бұндағы z - газдың жоғары сығылу коэффициенті .

4. Қатты фазаның аз деформациялануы салдарынан, әдетте, кеуектіліктің өзгерісі қысымның өзгерісінен сызықты тәуелді болады. Қабаттың көлемдік серпімділік коэффициентін енгізіп, жыныстардың сығылу заңы былай жазамыз:

(12)

бұндағы 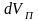- қысым dp-ға өзгергенде, V көлеміндегі қабат элементінде кеуектер көлемінің өзгеруі.

Сығылу заңын (11) былай жазуға болады:

немесе

(13)

5. Қысымының аз өзгерісі кезінде, өткізгіштіктің қысымнан тәуелділігін сызықты түрде былай жазамыз:

ал өзгеріс көп болса, экспоненциалды түрде былай жазамыз:

(14)

бұндағы 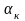–тәжірибе арқылы анықталатын коэффициент.

Негізгі әдебиеттер: Нег. 1[ 39-49 ]

Қосымша әдебиеттер: Қос. 3[ 44-51 ]

Бақылау сұрақтары:

1. Ағынның үздіксіздік теңдеуі.

2. Флюидтердің қозғалыс теңдеуі.

3. Флюидтердің күй теңдеуі.

4. Жыныстың күй теңдеуі.

№ 4 дәріс. Фильтрацияның дифференциалдық теңдеулері үшін негізгі бастапқы және шекті шарттардың түрлері – ұңғы түбін және қабаттың көректену аймағын моделдеу.

Өнімді қабатты немесе одан бөлініп шыққан бөлікті кеңістіктің белгілі бір ауданы ретінде қарастыруға болады, олардың шеттерін – шектер деп атайды. Шектер - флюидтер үшін өтімсіз болуы мүмкін. Мысалы, қабаттың жамылғы беті мен табаны, лықсыма сүйірленіп кему беті.

Шектік бет ретінде, қабаттың қоректену ауданымен (күндізгі жазықтықпен, табиғи суқоймамен) байланысты, су бетін айтуға болады.

Осы бетті басқаша қоректену өнбойы деуге болады. Ұңғы қабырғасы, қабаттың ішкі шегі болып саналады.

Теңдіктер жүйесінің шешімін алу үшін, оған алғашқы және шекті шартын енгізу керек.

Бастапқы шарт бойынша бастапқы деп алынған белгілі бір мезетте ізделінді функцияны беру барлық облыстарда жүргізіледі.

Мысалы, егер ізделінді функция қабат қысымы болса, онда бастапқы шарт мына түрде болады:

P= P (x, y, z), t=0 (1)

яғни,сондай-ақ, уақыттың бастапқы мезетінде, қысымның бүкіл қабатқа таралуы жүргізіледі.

Егер бастапқы мезетте қабат қозбаса, онда алғашқы шарт мына түрге келеді:

(2)

Шекті шарттар қабат шектерінде беріледі. Шекті шарттар саны, координаттар бойынша дифференциалды теңдеудің ретіне сәйкес болуы шарт.

Келесідей шекті шарттар болуы мүмкін (сур. 1).

ұңғы

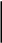
Г₁ Г₂ Г₂ Г₁

қабат коректену аймағы

ҰТА

1 -сурет. Қабаттың сыртқы және ішкі шекаралары

1. Сыртқы Г₁ шекарасында:

-қысым тұрақты

(3)

яғни, шек- қоректену өнбойы болып табылады.

-шек арқылы тұрақты ағын

(4)

мұндағы, n- Г-шегіне ұмтылған нормаль;

-шек арқылы айнымалы ағын

(5)

- тұйықталған сыртқы шек

(6)

-ұзына бойы шексіз қабат

(7)

2. Ішкі Г₂ шекарасында:

- радиусы 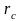ұнғы түбіндегі тұрақты қысым

(8)

- тұрақты шығым. Бұл шарт Дарси заңы орындалғанда былай жазамыз:

(9)

немесе r=r болғанда; (10)

мұндағы F = - ұңғының шеткі беттерінің ауданы; h – қабат қалыңдығы.

-ұңғы түбіндегі айнымалы қысым

P(r болғанда, r=r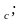 (11)

-айнымалы шығым

болғанда r=r ; (12)

-ұңғының істен шығуы

0 болғанда r=r . (13)

Негізгі әдебиеттер: Нег. 1[ 39-49 ]

Қосымша әдебиеттер: Қос. 3[ 44-51 ]

Бақылау сұрақтары:

1. Қоректену аймағы дегеніміз не?

2. Бастапқы шарты.

3. Шекті шарты.

4. Сыртқы және ішкі шарттар