13 Дәріс. Серпімді режим теориясының есептерін жуықтап шешу әдістері. Соколов – Гусейновтың орташалау әдісі.

Бүкіл қозған аймақ бойынша серпімді режимінің дифференциалдық теңдеуіндегі қысымнан туындысы уақыт бойынша орташаланады және кейбір функциямен ауыстырылады

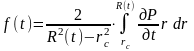. (1)

Оның мәні бастапқы және шекаралық шарттардан табылады. Сонда серпімді режимінің теңдеуі келесі түрге келеді:

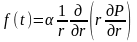, (2)

Тұрақты Q дебиті кезінде ұңғыға серпімді сұйықтың қалыптаспаған ағыны кезіндегі қысым таралуын анықтайық. Осы жағдайда түптегі және қозған аймақтың шекарасындағы шарттар (4)-(6) түрінде болады (12 дәрістегі).

(4)-(6) шарттар кезінде (2) теңдеуді r бойынша интегралдап табамыз;

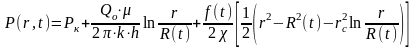, (3)

(6) шарттан анықтаймыз;

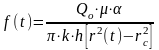, (4)

r²_c бар мүшелерді ескермей және (4) формуланы (3) формулаға қойып, табамыз

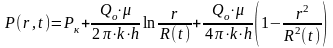. (5)

Қозган аймақтың R(t) координатын анықтау үшін (5) тендікті t бойынша дифференциалдау, нәтижесін (1) қою және (4) өрнекті ескеру керек. Сонда аламыз

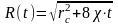. (6)

Сондықтан, қозған аймақтағы қысым таралуы (5) келесі түрде болады:

,

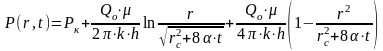при 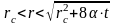. (7)

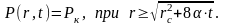
Негізгі әдебиет: 2 [133-150]

Қосымша әдебиет: 4 [277-283]

Бақылау сұрақтары:

1. Орташалау әдістің маңызы

14 Дәріс. Кеуекті ортада газдың қалыптаспаған фильтрациясын моделдеу. Скда әдіспен ұңғыға ғаздың құйылу туралы есебін жуықтап шешу.

Идеалды газдың қалыптаспаған фильтрациясының дифференциалды теңдеуін шығару үшін, осы теңдеудегі ажырамаушы ағынға фильтрацияның жылдамдық компонентіне және идеалды газдың күй теңдеуіне мәндер қойылады.

Кеуекті коэффициент - m , өткізгіштікті k - деп, газ тұтқырлығын - 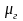әрдайым тұрақты деп мынаны аламыз:

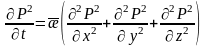, (1)

=>

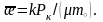
Ұңғымаға келетін газ ағыны туралы нақты есепті қарастырайық. Ол қабатта орналассын және де осы қабаттың шексіз созылымында ылғи да қалыңдығы h болсын.

1. дифференциялдық теңдеу осы жағдайда былай түрленеді:

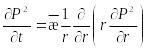(2)

Бұның шешілуі оның бастапқы және шекті шарттарына байланысты:

егер t=0

егер 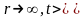0 (3)

Ұңғы түбіне мынадай шарт енгізейік массалық шығымы тұрақты - Q = const:

Q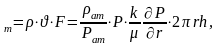

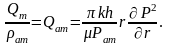
Онда

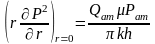(4)

Идеал газ бен серпімді сұйықтықтың қалыптаспаған сүзілгіш арасынан мынадай шешім шығарамыз. Идеал газ үшін квадратта қысым болу керек.

Сұйықтыққа арналған пьезоөткізгіштік 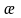коэффициент мынаған тең 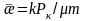, ал газ үшін коэффициент 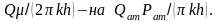Қалғаны бұрынғыдай қатынаста қалады.

(3)-ші мен (4)-ші формулаларды ескеріп (2)-ші формуланы былайша түрлендірейік:

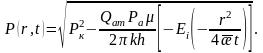(5)

Ұңғыма түбіне әсер етуші қысым өзгерісі (егер r= r_c)

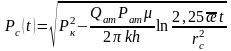(6)

СКДА тәсілі арқылы ұңғымаға келетін газ ағынына байланысты есепті шешу

Кез келген уақыт моментінде белгіленген аймақ – стационарлық заң бойынша радиусының ішінде қысым таралатын дөңгелекті аймақ болып табылады:

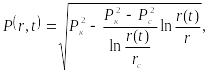
(7)

Белгіленген аймақтағы емес егер r>r(t) (8)

былай болса, онда белгіленген аймақтағыны былай қабылдаймыз:

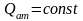егер (9)

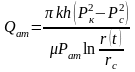(10)

(10)-ші формуладан

(11) (11) Осы алынған (11)-ші формуланы (7)-ші формулаға қойып, мынаны қорытып шығарамыз:

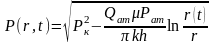(12)

r(t) – ны табу үшін материалдық баланс теңдеуін құрамыз.

r(t) радиусының зонасында қамтылатын газдың бастапқы қоры (егер ):

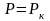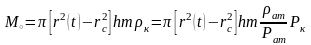(13)

Газ қорының ағымы

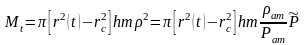(14)

мұнда

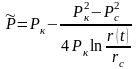(15)

Себебі газ шығымында әрдайым шығым тұрақты болады, онда

Олай болса (13), (14) және (15)-тен формулаларды ескерсек:

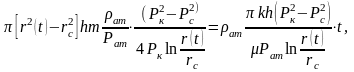
онда

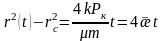
немесе 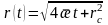(16)

(16)-шы формуланы (7)-шы формулаға қойсақ:

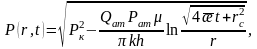
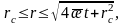
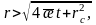(17)

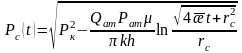(18)

Негізгі әдебиеттер: 1[170-184]

Қосымша әдебиеттер: 3[303-310]

Бақылау сұрақтары:

1. Газдың фильтрациясының дифференциалды теңдеуі.

2. Шығымы тұрақты болғандағы газ ұңғымасының қабырғасындаға қысым.

3. Стационар күйді дәйекті ауыстыру(СКДА) әдісінің мәні.

4. Материалдық баланс теңдеуі.

5. Газдың бастапқы қоры.

6. Ағымдағы газдың қоры.

15 дәріс. Екіфазды сұйықтық фильтрациясын моделдеу. Мұнайды сумен поршенділік ығыстыруы.

Кеуекті ортадағы екі сұйықтықтың шекара бөлімінің қозғалысы туралы есеп теориялық және практикалық қызығушылық туғызады.

Мұнай кен орнын су тегеурінді режим шартымен игеру жағдайында су шетінің тегеурін астында мұнайлылық контурдың созылуы байқалады.

Бірлесіп сұйықтың ығысу кезінде қозғалушы шекара бөліміне әсер етуші кинематикалық шарт.

Кеуекті ортадағы екі сұйықтың шекара бөлімінің қозғалысы туралы есепті дәлдікпен шешудің басты ауырлығы, сұйықтықтың шекара бөліміндегі тоқ сызықтарының сынуы.

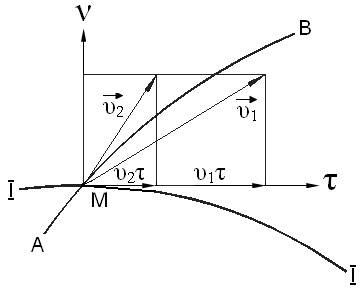
1 – сурет. Сұйықтың бөлінуінің шекарасындағы тоқ сызығының сынуы.

(1 суреттегі) I-I қисығы екі сұйықтықтың бөлімдерінің шекарасы болған. Олардың тұтқырлығы және және олар > (мұнай сумен ығыстырылады). Осы жердегі М нүктесі арқылы жанасушыны және нормальді сұйықтың бөлімінің шекарасына отырғызайық (I-I).

Мұнай мен судың сүзілгіштік жылдамдығының проекциясын табайық, ол берілген моментте М нүктесінде орналассын және де жанасушы және нормальді кеуекті ортадағы өткізгіштікті бөлім шекарасының екі жағында да әрдайым деп аламыз.

Ағын массасының ажырамайтын шартына сәйкес М нүктесіне кіретін бөліну шекарасының элементі арқылы қос сығылмайтын сұйықтықтардың қарапайым шығыны ішінара бір-бірімен тең болуы керек.

Осыдан, қос сұйықтықтың сүзілгіштіктерінің жылдамдықтарының нормальдарын құрайтындары тең болуы тиіс, яғни .

Сонымен қатар қос сұйықтыққа арналған қабаттағы М нүктесіндегі қысымда бірдей болғаны жөн, себебі ажыратылу жылдамдығының аздығынан (дыбыстықтан төмен) жазық ағында сол қысымның болмауы ғажап емес.

Қос сұйықтықтың сүзілгіштік жылдамдықтарының жанаушы құраушылары Дарси заңы бойынша анықталады.

(1)

(2)

> болғандықтан (1), (2)-ші формулалардан . Осыдан сүзілгіштік жылдамдықтың көрсеткіштік векторы МА тоқ сызығының жасасушысы үлкен вектор болады, МВ мұнай тоқ сызығының жанасуында.

Осыған байланысты АМ және МВ тоқ сызықтары (М нүктесі арқылы өтетін) сол М нүктесінде сыну қасиеті болады.

Сұйықтықтың бөлім шекарасындағы тоқ сызығының осы сынылудың ескерілуі осы шекара бөліміндегі есептің дәлме-дәл шығарылуының барысындағы басты қиындықты туғызады.

Берілген тоқ сызығы екі жағдайда ғана сынылмайды, олар: түзу сызықты паралельді және жазық радиалды. Осы екеуі шекара бөлімінің қозғалысы кезінде және болған жағдайда ғана іске асады. Осы есептер ең алдымен берілген параграфте қарастырылады. Осы жағдайда сұйықтар (мұнай мен су) сығылмайтын болып есептелінеді, бірге ерімейтін және химиялық кеуекті ортаның бір бірімен қабылдамайтын қасиетті айтамыз. Мұнайды сумен ығыстыру болжаумен алғанда толық жүргізіледі, яғни былайша айтқанда поршеньдік ығыстыру.