7.2. Корреляционный и регрессионный анализ
Задачи корреляционного анализа сводятся к следующему:
- измерение тесноты связи между варьирующими признаками;
- определение неизвестных причинных связей;
- оценка факторов, оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа есть:
- выбор типа модели (формы) связи;
- установление степени влияния независимых переменных на зависимую переменную (функцию регрессии);
- определение расчетных значений зависимой переменной.
Решение всех перечисленных задач приводит к необходимости комплексного использования корреляционного и регрессионного анализа. Статистическое моделирование связи между явлениями общественной жизни при этом состоит из следующих этапов.
1. Отбор факторных признаков для включения их в модель связи. В его основе лежит качественный и логический анализ явления, связанный с изучением его природы методами экономики, социологии.
2. Выбор типа модели связи (уравнения регрессии). Он может опираться на теоретические знания об изучаемом явлении, на опыт предыдущих аналогичных исследований или на анализ графического изображения статистических данных. Другим способом выбора уравнения регрессии является метод перебора различных уравнений с последующей статистической проверкой на основе t-критерия Стьюдента и F-критерия Фишера.
Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности. Исследователь должен стремиться к увеличению числа наблюдений, так как большой объем наблюдений обеспечивает адекватность статистических моделей.
Адекватность модели – соответствие теоретических величин фактическим статистическим данным.
3. Построение модели связи, т.е.
определение неизвестных параметров
множественной регрессии
,
,...,
.
Неизвестные определяются по методу
наименьших квадратов, в котором в
качестве решения принимается точка
минимума суммы квадратов отклонений
эмпирических данных
от выравненных
:
.
Для определения минимума данной функции приравнивают к нулю её частные производные и получают систему нормальных уравнений для нахождения , ,..., .
Так, для расчета параметров линейной двухфакторной регрессии
система нормальных уравнений будет иметь вид:
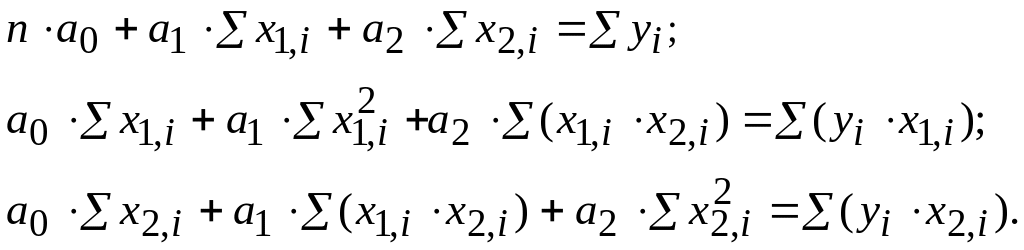
Параметры системы могут быть найдены методами численного моделирования (например, методом Гаусса) или с помощью прикладных программ (Eureka, MathCad, Excel и др.).
4. Оценка существенности корреляции. Для этого рассчитывают разного рода характеристики тесноты связи между зависимой и независимой переменными: парные, частные и множественные коэффициенты корреляции, множественный коэффициент детерминации.
5. Проверка адекватности полученной модели связи, которая заключается в оценке значимости коэффициентов регрессии и уравнения регрессии. Она осуществляется на основе t-критерия Стьюдента и F-критерия Фишера.
6. Экономическая интерпретация коэффициентов уравнения регрессии. Она вновь связана с качественными особенностями изучаемого явления. При этом вычисляются частные коэффициенты эластичности, β-коэффициенты.