
- •Введение
- •Глава 1. Задачи статистики и ее организация
- •1.1. Предмет, методы и задачи статистики
- •1.2. Современная организация статистики в Российской Федерации и ее задачи [6]
- •1.3. Источники статистической информации. Формирование информационной базы статистического исследования
- •1.3.1. Отчетность предприятий
- •1.3.2. Регистр организаций и предприятий
- •1.3.3. Переписи и обследования
- •1.3.4. Административные источники
- •1.3.5. Денежная и банковская статистика
- •1.3.6. Платежный баланс
- •1.3.7. Таможенная статистика
- •Контрольные вопросы для самопроверки
- •Глава 2. Статистическое наблюдение
- •2.1. Задачи статистического наблюдения
- •2.2. Организационные формы статистического наблюдения
- •2.3. Контроль материалов наблюдений
- •2.4. Основные категории статистики
- •Контрольные вопросы для самопроверки
- •Глава 3. Группировка статистических данных и ее роль в анализе информации
- •3.1. Сводка и группировка статистических материалов
- •Статистические наблюдения дают лишь исходный материал. Для получения характеристик объекта необходимо произвести сводку материала статистического наблюдения.
- •3.2. Виды группировок
- •3.3. Система группировок
- •Величина равного интервала вычисляется по формуле
- •3.4. Организация и техника проведения сводки
- •3.5. Виды рядов распределения
- •Контрольные вопросы для самопроверки
- •Глава 4. Абсолютные, относительные и средние статистические величины
- •4.1. Абсолютные статистические величины
- •Статистические величины – это некоторая количественная категория, с помощью которой измеряются явления общественной жизни. Статистические величины бывают абсолютными, относительными и средними.
- •4.2. Относительные статистические величины
- •4.3. Средние величины
- •4.4. Структурные средние величины
- •Контрольные вопросы для самопроверки
- •Глава 5. Показатели вариации признака
- •5.1. Показатели вариации
- •5.2. Моменты распределения
- •5.3. Сложение дисперсий изучаемого признака
- •5.4. Дисперсия альтернативного признака
- •5.5. Показатели формы распределения
- •5.6. Кривые распределения
- •Контрольные вопросы для самопроверки
- •Глава 6. Выборочное наблюдение
- •6.1. Понятие о выборочном наблюдении
- •6.2. Виды и схемы отбора единиц наблюдения в выборку
- •6.3. Ошибки выборки
- •Контрольные вопросы для самопроверки
- •Глава 7. Статистическое изучение взаимосвязей
- •7.1. Виды связей между явлениями
- •7.2. Корреляционный и регрессионный анализ
- •7.3. Оценка существенности корреляции
- •7.4. Проверка адекватности модели связи. Принятие решений на основе уравнения регрессии
- •7.5. Экономическая интерпретация регрессионной модели
- •Контрольные вопросы для самопроверки
- •Глава 8. Ряды динамики
- •8.1. Ряды динамики и их виды
- •8.2. Правила построения рядов динамики
- •8.3. Показатели анализа динамического ряда
- •Интервальный ряд моментный ряд
- •Года t: 1991 1992 1993 1994
- •Цепные базисные (1991 г.)
- •Цепные базисные (1991 г.)
- •8.4. Методы анализа тенденции развития в рядах динамики
- •8.5. Прогнозирование развития социально-экономических явлений на основе тренда
- •8.6. Методы изучения сезонных колебаний
- •Контрольные вопросы для самопроверки
- •Глава 9: экономические индексы
- •9.1. Общие понятия об индексах и значение метода индексного анализа
- •Если уровни сравниваются:
- •9.2. Классификация индексов
- •9.3. Правила построения экономических индексов
- •9.4. Индивидуальные и общие индексы в агрегатной
- •Форме. Экономический анализ
- •Индекс физического объема реализации:
- •Индекс себестоимости:
- •Индекс затрат на производство:
- •Индекс производительности труда:
- •9.5. Общие индексы в средней форме
- •9.6. Системы индексов
- •Системы индивидуальных индексов
- •Индекс физического объема:
- •Система общих индексов в агрегатной форме
- •Контрольные вопросы для самопроверки
- •Библиографический список
- •Общая теория статистики
6.3. Ошибки выборки
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.
Теорема
П.Л. Чебышева
утверждает принципиальную возможность
определения генеральной средней по
данным случайной повторной выборки.
Теорема Чебышева дополняется теоремой
А.М. Ляпунова,
которая позволяет рассчитать максимальную
ошибку выборочной средней при данном
достаточно большом числе независимых
наблюдений в генеральной совокупности
с конечной средней и ограниченной
дисперсией вероятности того, что
расхождение между выборочной и генеральной
средней
![]() не превзойдет по абсолютной величине
некоторую величину
не превзойдет по абсолютной величине
некоторую величину
![]() ,
равную интегралу
Лапласа. Это
можно записать следующим образом:
,
равную интегралу
Лапласа. Это
можно записать следующим образом:
![]() ;
;
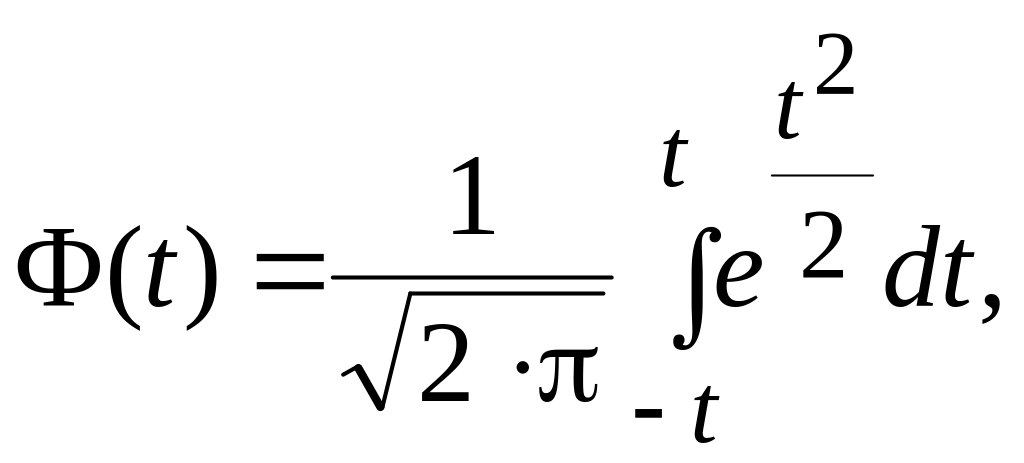
где
![]() – интеграл Лапласа (нормированная
функция Лапласа).
– интеграл Лапласа (нормированная
функция Лапласа).
Величина , обозначаемая , называется предельной ошибкой выборки. Различают среднюю и предельную ошибки выборки. Эти два вида ошибок связаны следующим соотношением:
![]() ,
,
где – предельная ошибка выборки; – средняя ошибка выборки; t – коэффициент доверия, определяемый в зависимости от уровня вероятности.
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.
Так, при случайном отборе средняя ошибка определяется по формулам:
1)
при повторном отборе:
![]() ;
;
2)
при бесповторном отборе:
![]() ,
,
где
![]() – выборочная (или генеральная) дисперсия;
– выборочное (или генеральное) среднее
квадратическое отклонение; n
– объем выборочной совокупности; N
– объем генеральной совокупности.
– выборочная (или генеральная) дисперсия;
– выборочное (или генеральное) среднее
квадратическое отклонение; n
– объем выборочной совокупности; N
– объем генеральной совокупности.
Можно определить предельные ошибки выборки и для доли признака. В этом случае дисперсия доли определяется по формуле
![]()
где
![]() –
доля единиц, обладающих данным признаком
в выборочной совокупности.
–
доля единиц, обладающих данным признаком
в выборочной совокупности.
Тогда при случайном отборе предельная
ошибка
![]() может вычисляться по формуле:
может вычисляться по формуле:
1) при повторном отборе:
![]() ;
;
2) при бесповторном отборе:
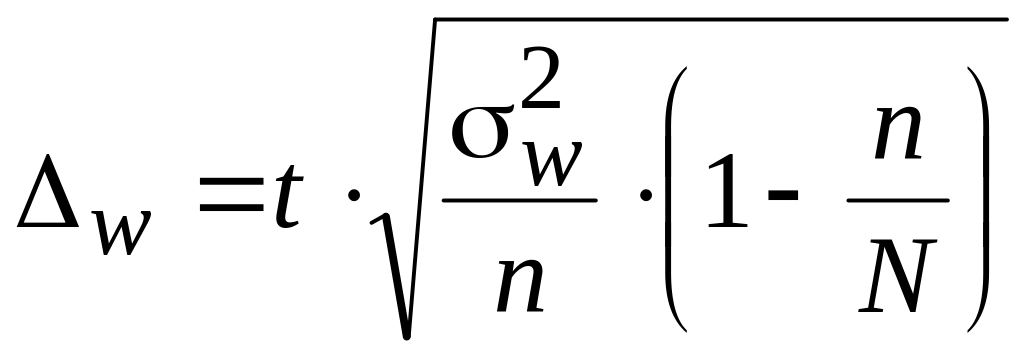 .
.
Пределы доли признака в генеральной совокупности определяются следующим образом:
![]() .
.
При расчете ошибок возникает существенное затруднение, так как величины и p по генеральной совокупности неизвестны. Эти величины в условиях большой выборки заменяют величиной S (выборочная дисперсия) и w (выборочная доля), рассчитанными по выборочным данным.
Формулы предельной ошибки позволяют решать задачи трех видов.
Определение пределов генеральных характеристик с заданной степенью надежности (доверительной вероятностью).
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
![]() ;
;
![]() ,
,
где и – генеральная и выборочная среднее соответственно; – предельная ошибка выборочной средней.
Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину.
Доверительная вероятность является функцией от t , определенной по формуле
![]() .
.
По величине t определяется доверительная вероятность . На практике пользуются готовыми таблицами этой функции . В табл. 6.1 приведены некоторые значения t и .
Таблица 6.1. Значения вероятности для коэффициента доверия t
t |
1,000 |
1,5 |
2,0 |
2,5 |
2,6 |
3,0 |
4,0 |
|
0,683 |
0,867 |
0,954 |
0,988 |
0,991 |
0,997 |
0,9999 |
Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.
Объем выборки можно вычислить по следующим формулам.
Случайная и механическая выборка:
1)
повторная:
![]() ;
;
2)
бесповторная:
![]() .
.
Покажем практическое применение рассмотренной выше методики на следующих примерах.
Пример 6.1. [7] При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.
Решение.
Для
вероятности
= 0,997
определяем по табл. 6.1 значение
коэффициента доверия t
= 3. Объем выборки n
= 200 и
![]() = 4.
= 4.
Рассчитаем предельную ошибку выборки:
![]() =
=
![]() = 3 4/
= 3 4/![]() = 0,84.
= 0,84.
Определим пределы генеральной средней:
30 – 0,84 < х < 30 + 0,84,
или 29,16 < х< 30,84.
Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 до 30,84 г.
Пример 6.2. [7] С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью рабочих 480 человек была проведена 25 %-ная механическая выборка. По результатам наблюдения оказалось, что у 10 % обследованных рабочих потери рабочего времени составили более 45 минут в день. С вероятностью 0,683 установить пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 минут в день.
Решение. Определяем объем выборочной совокупности:
n = 480![]() =
120 человек.
=
120 человек.
Выборочная доля w равна по условию 10 %. По табл. 6.1 определяем, что для вероятности = 0,683 коэффициент доверия t = 1. Учитывая, что при достаточно большой совокупности механический отбор по точности результатов близок к случайному отбору, для определения средней ошибки используем выше приведенные формулы:
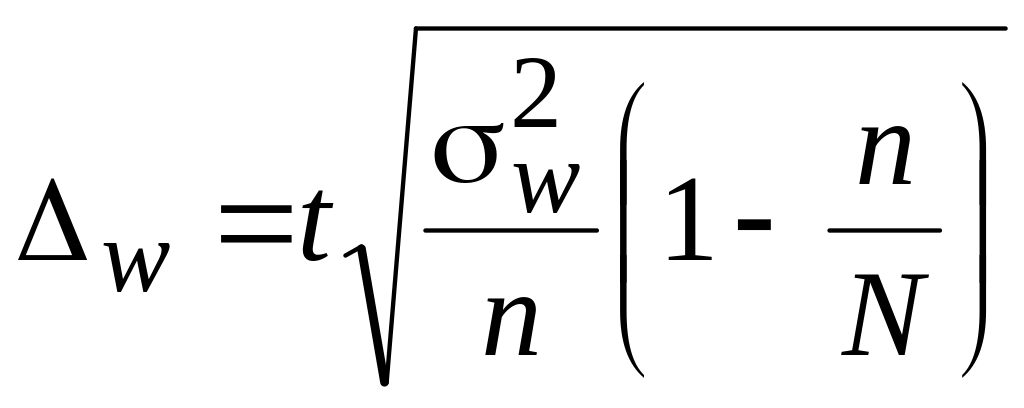 =
=
![]() или 2,4 %.
или 2,4 %.
Пределы доли признака в генеральной совокупности:
10 – 2,4 p 10 + 2,4,
или
7,6 p 12,4.
Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями времени более 45 минут в день находится в пределах от 7,6 до 12,4 %.
Ошибки и пределы генеральных характеристик
при других способах формирования
выборочной совокупности определяются
на основе формул, отражающих особенности
этих видов выборки. В случае типической
выборки показателем вариации является
средняя из внутригрупповых дисперсий
![]() ,
при серийной выборке – межгрупповая
дисперсия
,
при серийной выборке – межгрупповая
дисперсия
![]() .
.
Для типической выборки средняя ошибка вычисляется по формулам:
1) при отборе, пропорциональном объему типических групп:
![]() – повторный
отбор;
– повторный
отбор;
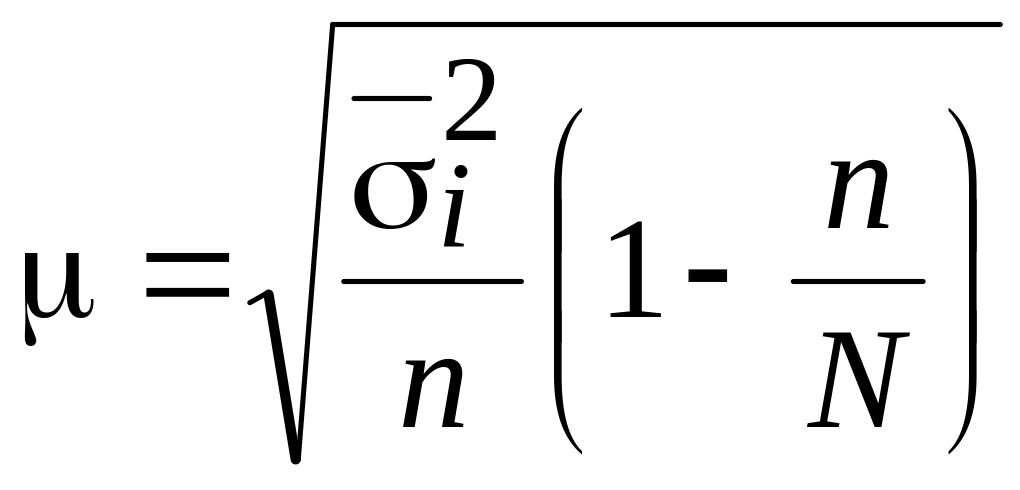 – бесповторный
отбор;
– бесповторный
отбор;
2) при отборе, непропорциональном объему групп:
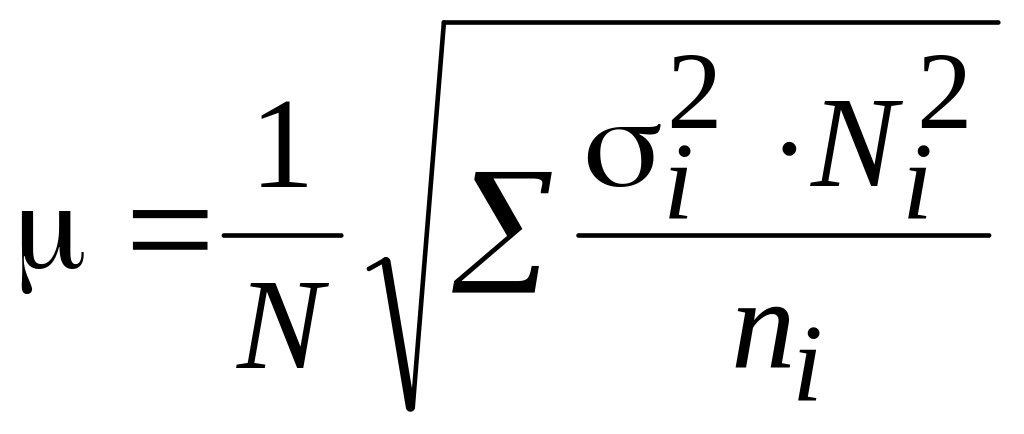 – повторный
отбор;
– повторный
отбор;
 – бесповторный
отбор,
– бесповторный
отбор,
где
Ni,
ni
– объемы i-й
типической группы и выборки из нее
соответственно;
![]() – групповые дисперсии.
– групповые дисперсии.
При серийной выборке средняя ошибка определяется следующим образом:
![]() – повторный
отбор;
– повторный
отбор;
![]() – бесповторный
отбор,
– бесповторный
отбор,
где r – число серий в выборочной совокупности; R – число серий генеральной совокупности; 2 – межгрупповая, межсерийная дисперсии;
![]() .
.
Пример 6.3. [7] В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние урожайности по районам составили соответственно: 14,5; 16; 15,5; 15; 14 ц/га. С вероятностью 0,954 найти пределы урожайности во всей области:
![]()
Решение. Рассчитаем общую среднюю:
Межгрупповая дисперсия:
![]()
Определяем предельную ошибку серийной бесповторной выборки (t = 2, P = 0,954):
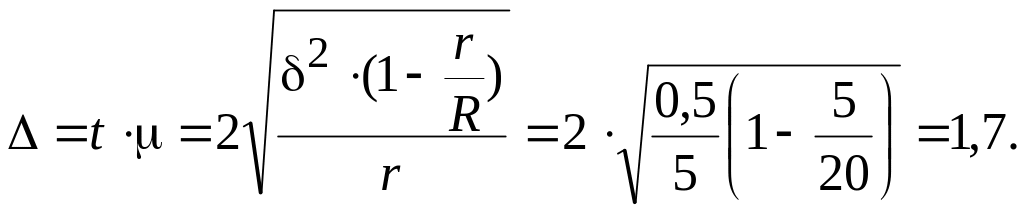
Урожайность в области с вероятностью 0,954 будет находиться в пределах:
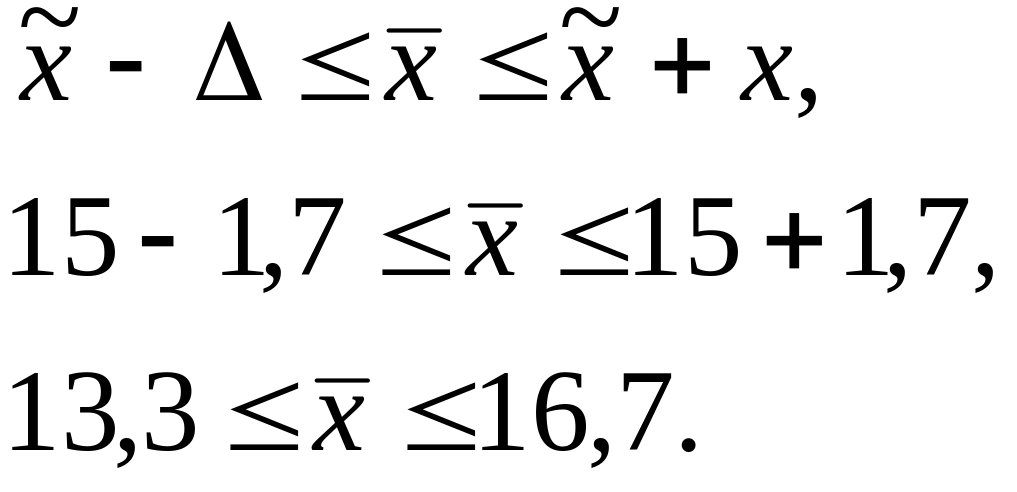
Следовательно, урожайность в области с вероятностью 0,954 будет находится в пределах от 13,3 до 16,7 ц/га.
Объем выборки можно вычислить следующим образом.
1. Типическая выборка:
повторный
отбор –
![]() ;
;
бесповторный
отбор –
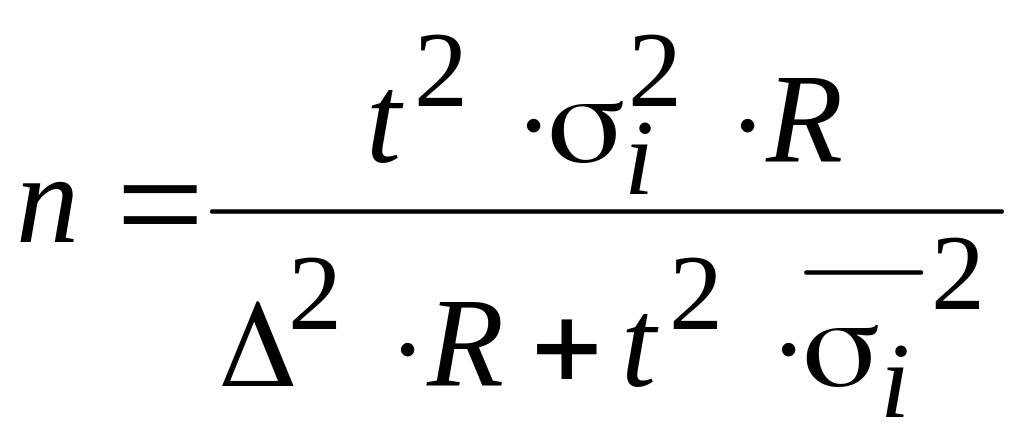 .
.
2. Серийная выборка:
повторный
отбор –
![]() ;
;
бесповторный
отбор –
![]() .
.
Пример 6.4. [7] В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала трех путевок, если по данным пробного обследования дисперсия составляет 225?
Решение. По табл. 6.1 определяем для вероятности = 0,683 коэффициент доверия t = 1.
Рассчитаем необходимый объем выборки:
 =
=
![]() .
.
Следовательно, нужно обследовать 20 агентств, чтобы с вероятностью 0,683 ошибка не превышала трех путевок.
Пример 6.5. [7] С целью определения доли сотрудников коммерческих банков в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников 12000 человек, в том числе 7000 мужчин, 5000 женщин.
На основе предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определить необходимый объем выборки при вероятности 0,997 и ошибке 5 %.
Решение. Рассчитаем общую численность типической выборки:
Для вероятности = 0,997 коэффициент t = 3 (табл. 6.1). Число серий генеральной совокупности – это общее число сотрудников (R = 12000).
![]() чел.
чел.
Вычислим объем отдельных типических групп:
мужчины
=
![]() человек;
человек;
женщины
=
![]() человек.
человек.
Таким образом, необходимый объем выборочной совокупности сотрудников коммерческих банков составляет 550 человек, в том числе 319 мужчин и 231 женщина.
