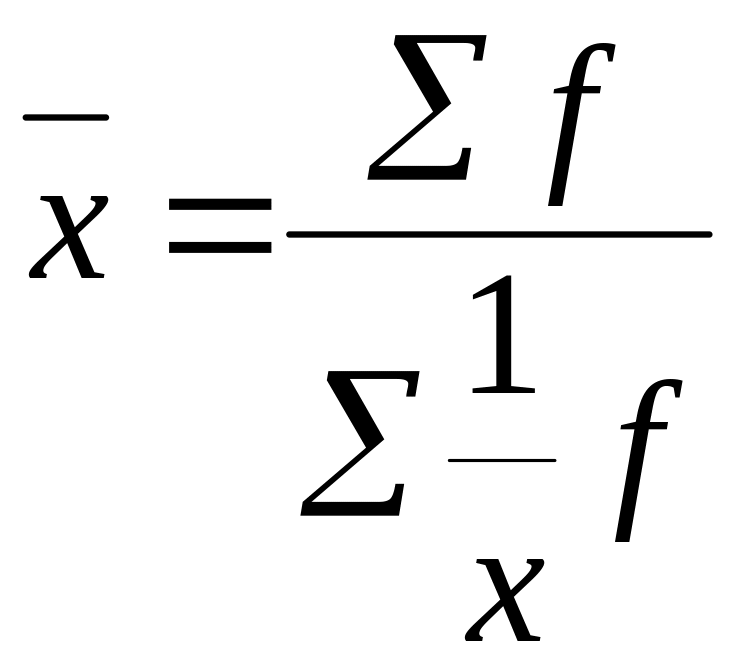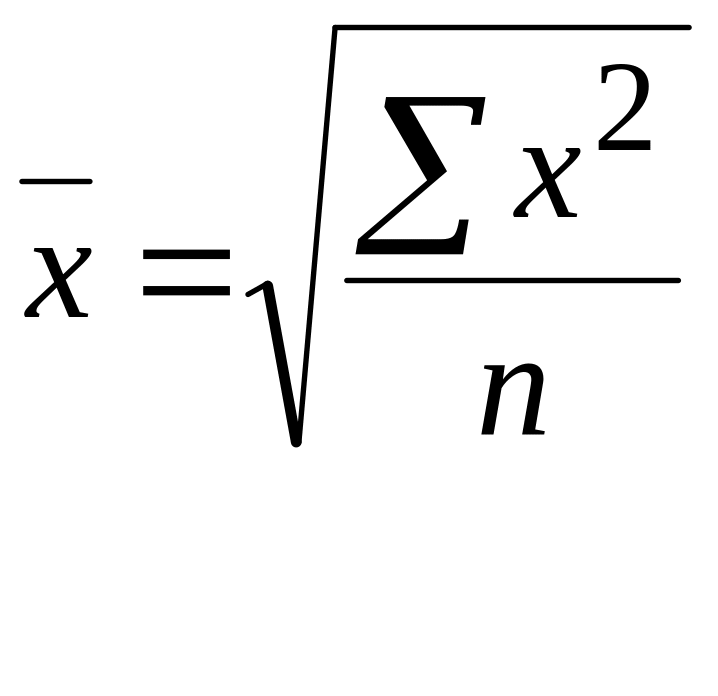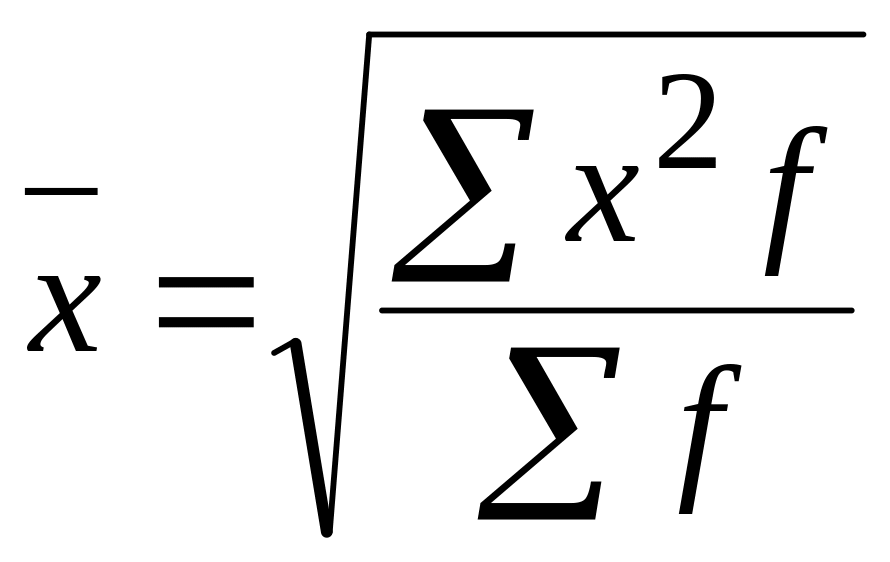4.3. Средние величины

Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.

Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие – для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.

При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.

В экономических исследованиях и плановых расчетах применяются две категории средних:

• степенные средние;

• структурные средние.

К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая.

Средняя обозначается через .

Общая формула степенной средней записывается следующим образом:

,

где f_i – частота (повторяемость индивидуальных значений признака); х_i – величины, по которым вычисляется средняя.

В зависимости от степени k получаются различные виды средних величин, их формулы представлены в табл. 4.4.

Таблица 4.4. Формулы расчета различных видов степенных средних величин

Значение k	Наименование средней	Формулы средней
		простая	взвешенная
–1	Гармоническая		;
0	Геометрическая
1	Арифметическая
2	Квадратическая

Как видно из данных табл. 4.4, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т.е. умножают на нее. Частоты при этом называются статистическими весами или просто весами средней. В качестве веса могут применяться какие-либо другие величины (в табл. 4.4 они обозначены буквой W). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными – частостями (относительные частоты).

Величины степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака при различных значениях степени (k), не одинаковы. Чем больше показатель степени k, тем больше значение средней величины. Таким образом, выполняется правило мажорантности средних:

< < < .

Какую среднюю вычислять – решается в каждом отдельном случае, исходя из задачи исследования и наличия исходной информации. Чаще всего используется средне арифметическая и средне гармоническая. Они используются в плановых расчетах, при расчете общей средней и средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Средняя арифметическая применяется в тех случаях, когда известны варианты варьирующего признака и их частот.

Средняя арифметическая обладает следующими математическими свойствами:

1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

.

2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

.

3. Если варианты значений признака уменьшить или увеличить на постоянное число A, то средняя арифметическая соответственно уменьшится или увеличится на эту величину:

.

4. Если все варианты значений уменьшить или увеличить в A раз, то средняя также соответственно увеличится или уменьшится в A раз:

.

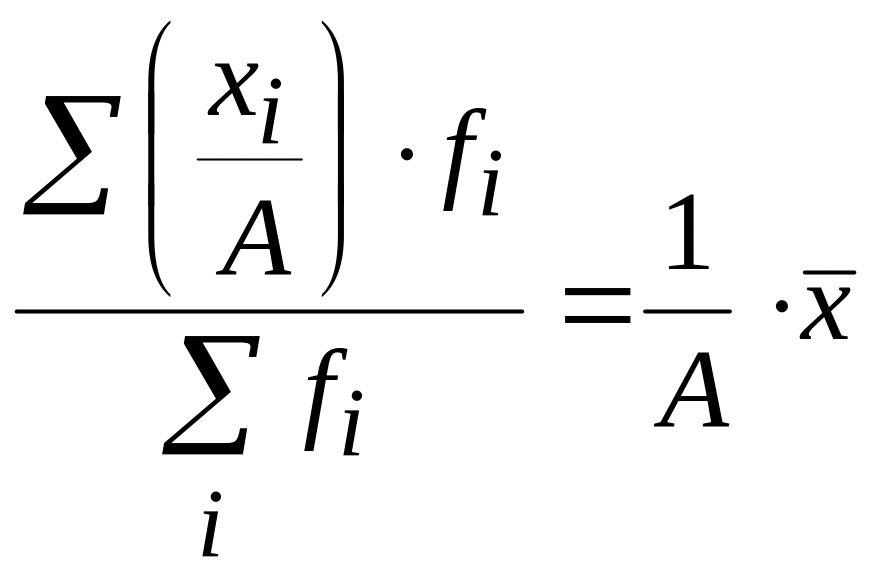5. Если все частоты уменьшить или увеличить в A раз, то средняя арифметическая от этого не изменится:

.

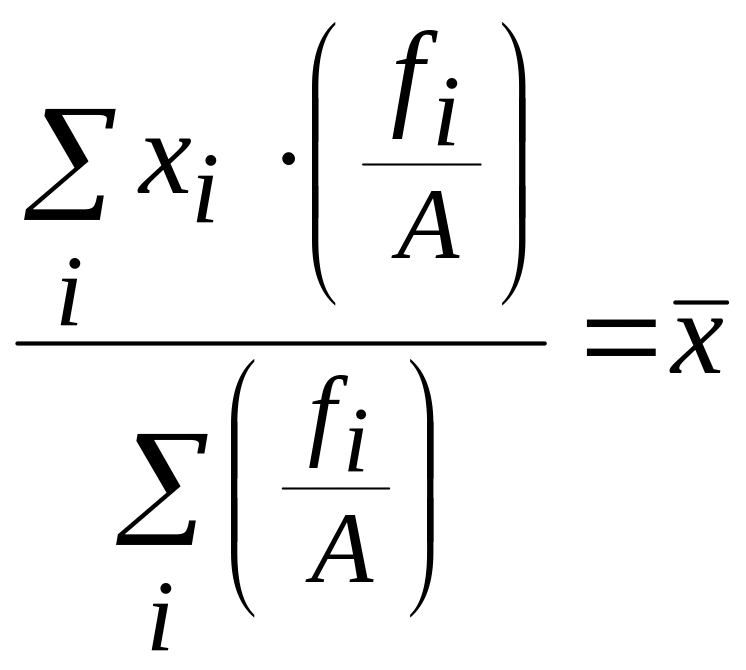Пример 4.4. В бригаде из трех рабочих зарплата распределяется следующим образом:

1. Иванов – 3000 рублей

2. Петров – 3200 рублей.

3. Сидоров – 4000 рублей.

Нужно определить среднюю зарплату в бригаде. Для решения задачи использовалась формула простой средней арифметической:

= (3000 + 3200 + 4000) / 3 = 3400.

Пример 4.5. Распределение служащих фирмы по стажу работы представлено в табл. 4.5.

Таблица 4.5. Распределение рабочих участка по стажу работы

Стаж работы, лет	До 5 лет	5–10	10–15	15 и более
Количество служащих, человек	10	6	12	3

Определить средний стаж работы рабочих участка.

Решение:

Прежде чем вычислить , необходимо для каждого интервала предварительно вычислить среднее значение признака как полусуммы нижнего и верхнего значений интервала – . Величина открытых интервалов приравнивается к величине примыкающих к ним соседних интервалов:

; ; ; .

Для вычисления среднего стажа рабочих используем формулу средней арифметической взвешенной:

.

Средний стаж работы равен:

лет.

Средняя арифметическая взвешенная применяется для вычисления общей средней по групповым средним.

Пример 4.6. По данным о числе вкладчиков и размере вклада за 1 квар-тал 2005 года по 3 филиалам Сбербанка района города (табл. 4.6), определить средний размер вклада (на 30.03.2005 г.).

Таблица 4.6. Число вкладчиков и размер вклада за 1 квартал 2005 г.

по трем филиалам Сбербанка

№ филиала Сбербанка	Число вкладчиков, чел.	Средний остаток по вкладу, млн. руб
1	1350	1,5
2	2050	2,05
3	1290	1,81

Для определения среднего остатка вклада по трем филиалам в целом следует общую сумму остатков по вкладу для всех вкладчиков разделить на общее число вкладчиков.

,

где x_i – среднее значение признака по каждой группе (в нашем случае – средний остаток по вкладу отдельного филиала); w_i – веса средней (число вкладчиков по каждому филиалу);

млн. руб.

Когда статистическая информация не содержит частот f по отдельным вариантам x совокупности, а представлена как их произведение , применяется формула средней гармонической взвешенной.

Пример 4.7. Есть следующие данные о фонде зарплаты и средней зарплаты за ноябрь месяц по цехам предприятия (табл. 4.7.)

Таблица 4.7. Средняя зарплата и фонд заработной платы

за ноябрь месяц по цехам предприятия

№ цеха	Ноябрь
	Средняя заработная плата, руб.	Фонд заработной платы, руб.
1	3600	48600
2	3580	75180
3	3340	83500

Определить среднюю месячную заработную плату работников предприятия.

Решение:

Условные обозначения следующие:

w – фонд заработной платы по каждому цеху;

х – средняя месячная заработная плата работников каждого цеха.

Средняя заработная плата в ноябре исчислена по формуле средней взвешенной гармонической:

руб.,

где – численность работников каждого цеха за ноябрь.

Следовательно, средняя месячная заработная плата работников предприятия в ноябре 3483,7 руб.

Пример 4.8. Автомобиль прошел первые 200 км со скоростью 75 км/ч, а оставшиеся 130 км со скоростью 85 км/ч. Определить среднюю скорость автомобиля на протяжении всего пути в 330 км.

Решение:

Условные обозначения следующие:

– фонд заработной платы по каждому цеху;

– средняя скорость автомобиля на отдельных участках пути;

– затраты времени на прохождения отдельных участков пути.

Средняя скорость определяется как частное от деления всего пути ( = 200 + 130) на общие затраты времени:

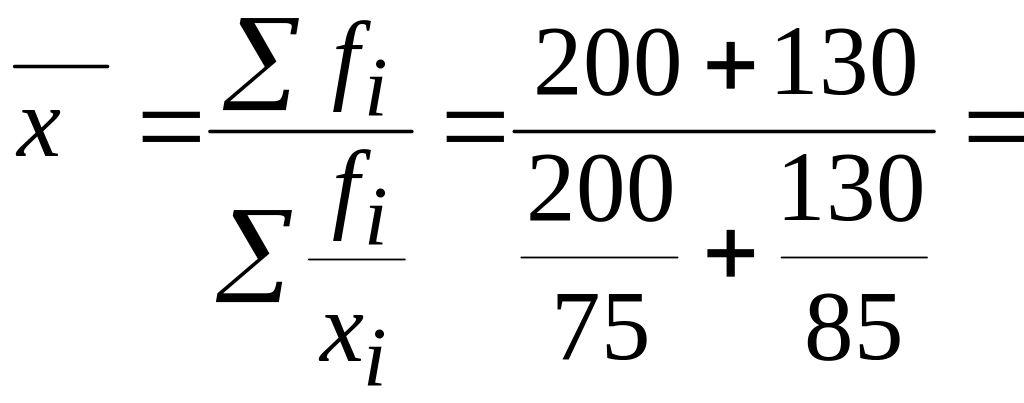
км/ч.

Следовательно, средняя скорость автомобиля на протяжении всего пути была 78,65 км/ч.

В том случае, если объемы явлений, т.е. произведения, по каждому признаку равны, применяется средняя гармоническая простая. Ее применяют при вычислении средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовление одного и того же вида продукции, одной и той же детали, изделия.

Пример 4.9. Две машины прошли один и тот же путь: одна со скоростью 70 км/ч, вторая – 85 км/ч. Определить среднюю скорость автомобилей.

Решение:

Средняя скорость исчисляется по формуле средней гармонической простой:

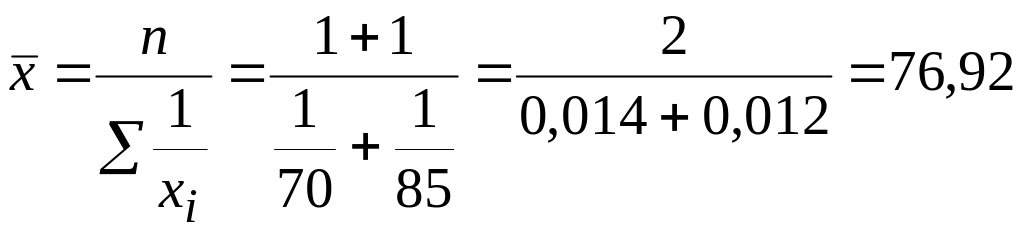км/ч.

Следовательно, средняя скорость автомобилей 76,92 км/ч.

Средняя квадратическая применяется для расчета среднего квадратического отклонения , являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).

Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики, если промежутки времени, к которым относятся коэффициенты роста, одинаковы. Если средние коэффициенты роста относятся к периодам различной продолжительности, то общий средний коэффициент роста за весь период определяется по формуле средней геометрической взвешенной (f – продолжительность периода, к которому относится средний коэффициент роста).

Пример 4.10. Выпуск продукции предприятия в течение четырех лет представлен в табл. 4.8.

Таблица 4.8. Выпуск продукции предприятием

Год	Продукция, тыс. руб.	Коэффициент роста
1999	500	–
2000	650	1,3
2001	780	1,2
2002	792	1,02

Среднее значение коэффициента роста определяется по формуле средней геометрической:

.

Средний темп роста выпуска продукции за четыре года составил 116,7 .
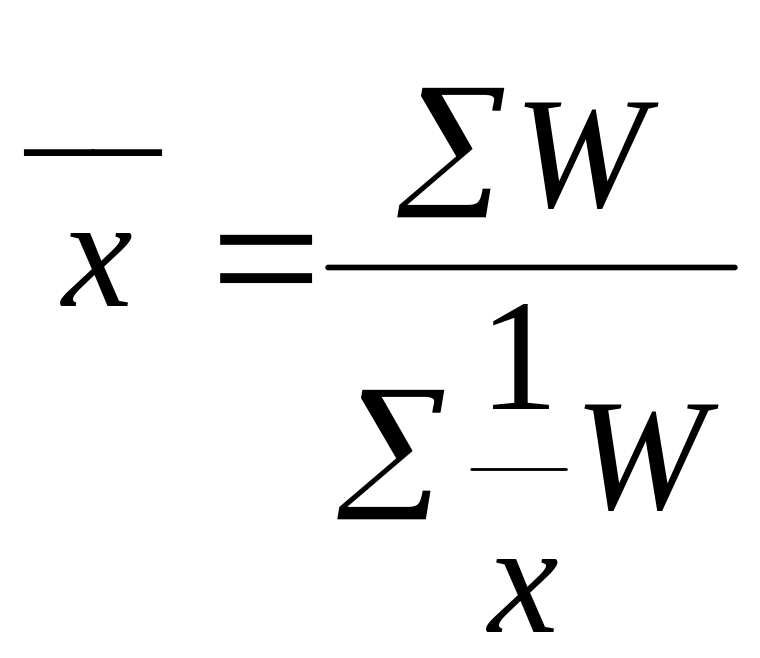