1.5. Экономическая интерпретация

многофакторной регрессионной модели

Интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков, т.е. с выяснения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый. Особое значение имеет знак перед коэффициентом регрессии; он говорит о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает; если факторный признак со знаком минус, то с его увеличением результативный признак уменьшается. Интерпретация этих знаков определяется социально-экономическим содержанием результативного признака.

Однако на основе коэффициентов регрессии нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак, так как коэффициенты регрессии между собой не сопоставимы, поскольку они измерены разными единицами. На их основе нельзя также установить, в развитии каких факторных признаков заложены наиболее крупные резервы изменения результативного показателя.

С целью расширения возможностей экономического анализа используются следующие величины.

Частные коэффициенты эластичности, устраняющие различия в единицах измерения факторов, определяются как:

, (1.21)

где - коэффициент регрессии при j – м факторе;

- среднее значение j – го фактора;

- среднее значение результативного признака.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель при изменении на 1 % каждого фактора при фиксированном значении других факторов.

С помощью β - коэффициентов определяют факторы, в которых заложены наиболее крупные резервы улучшения изучаемого показателя. β - коэффициенты учитывают различия в степени варьирования вошедших в уравнение факторов и вычисляются по формуле:

, (1.22)

где - среднее квадратическое отклонение j – го фактора;

- среднее квадратическое отклонение результативного признака.

β - коэффициенты показывают, на какую часть среднего квадратического отклонения изменяется результативный признак с изменением соответствующего факторного признака на величину его среднего квадратического отклонения.

Δ – коэффициенты рассчитываются по формуле:

. (1.23)

Δ – коэффициенты показывают, какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов.

1.6. Решение типовых задач

Задание 1. Данные о выработке деталей за смену 20 рабочими цеха представлены в таблице 1.3. Исследовать зависимость производительности труда от внутрисменных простоев и квалификации рабочих. Для этого:

1) выполнить качественный и логический анализ явления;

2) выбрать тип модели связи;

3) определить неизвестные параметры множественной регрессии по методу наименьших квадратов;

4) оценить существенность корреляции, рассчитав парные, частные и множественные коэффициенты корреляции, множественный коэффициент детерминации;

5) проверить адекватность модели связи на основе t - критерия Стьюдента и F – критерия Фишера;

6) дать экономическую интерпретацию регрессионной модели на основе анализа коэффициентов регрессии, частных коэффициентов эластичности, β – и Δ – коэффициентов.

Таблица 1.3

Порядковый номер рабочего	Внутрисменные простои, мин.	Квалификация рабочего (тарифный разряд)	Дневная выработка рабочего, шт. y
1	5	3	86
2	8	4	88
3	15	5	94
…	…	…	…
19	20	2	77
20	14	4	92
Итого	220	80	1800

Порядок выполнения задания

1) Факторными признаками являются внутрисменные простои и квалификация рабочих .

Результативный признак - производительность труда, т.е. дневная выработка рабочего y.

Теоретический анализ исходных данных позволяет установить наличие причинно-следственной связи факторных признаков с результативным показателем.

2) Так как имеются два факторных признака, то регрессионная модель связи будет двухфакторная. Рассмотрим линейную модель:

.

3) По исходным данным построим систему нормальных уравнений (1.7) для определения неизвестных коэффициентов регрессии , , . Предварительно рассчитаем вспомогательные величины (для простоты записи в формулах опустим индекс суммирования):

n = 20; ; ; ; ;

; ; ; .

Система нормальных уравнений имеет вид:

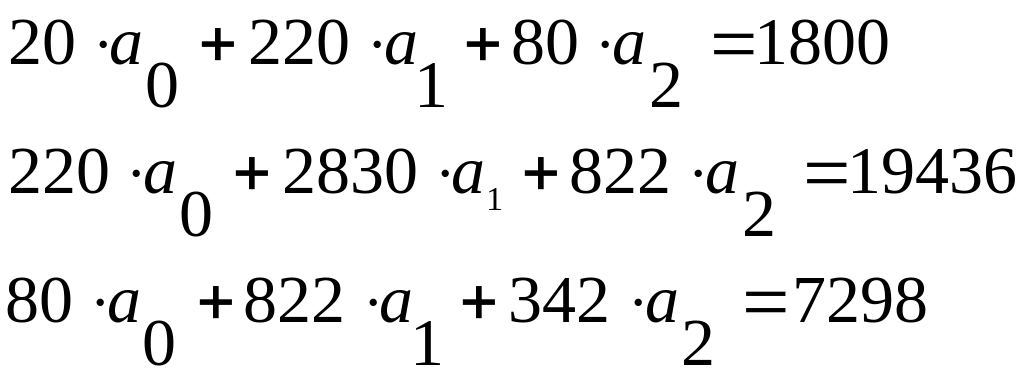
Решая данную систему, получаем

; ; .

Уравнение множественной регрессии, выражающее зависимость производительности труда y от внутрисменных простоев и квалификации рабочих , есть:

. (1.24)

4) Оценим существенность корреляции.

а) Рассчитаем парные коэффициенты корреляции по формулам (1.10) - (1.12). Предварительно определим вспомогательные величины:

; ; ; ; ;

; ; ; .

Средние квадратические отклонения вычислим по формулам (1.13):

; ;

.

Тогда парные коэффициенты корреляции будут равны:

; ;

.

Проанализируем полученные значения, используя табл. 1.1 и 1.2. Видно, что связь между

- производительностью труда и внутрисменными простоями вероятностная, обратная (т.е. с увеличением простоев дневная выработка падает), сильная;

- производительностью труда и квалификацией рабочих вероятностная, прямая, сильная;

- внутрисменными простоями и квалификацией рабочих вероятностная, обратная (более квалифицированный рабочий допустит меньше простоев), умеренная, если, конечно, учитывать влияние на эти факторы результативного признака - необходимости выполнения задания.

б) Определяем частные коэффициенты корреляции первого порядка, используя формулы (1.14) – (1.16).

;

;

.

Видно, что выводы о характере и направлении связи в данном случае не противоречат выводам, сделанным при анализе парных коэффициентов корреляции. Однако связь каждого фактора с изучаемым показателем при условии комплексного воздействия факторов становится слабее. Практически отсутствует взаимосвязь между факторными признаками при элиминировании результативного показателя ( ). Это вполне понятно: если не стоит вопрос о выполнении плана, то внутрисменные простои и квалификация рабочих никак не связаны между собой.

в) Рассчитаем множественный коэффициент корреляции (см. формулу (1.17)):

г) Множественный коэффициент детерминации или 74,9 %.

Он показывает, что вариация производительности труда на 74,9 % обусловливается двумя анализируемыми факторами. Это означает, что выбранные факторы существенно влияют на показатель производительности труда. Таким образом, изучаемая с помощью многофакторного корреляционного и регрессионного анализа вероятностная связь между исследуемыми показателями говорит о целесообразности построения двухфакторной регрессионной модели производительности труда в виде линейного уравнения регрессии.

6) Проверим адекватность построенной двухфакторной модели производительности труда.

а) Значимость , и оценим на основе t - критерия Стьюдента по формулам (1.18) – (1.19) (n = 20, k = 2):

;

;

.

Для расчета определим следующие величины:

- число степеней свободы ν = n – k – 1 = 20 – 2 – 1 = 17;

- уровень значимости = 0,05 (т.е. определим результат с вероятностью 95%).

По табл. П1 Приложения 1 находим, что . Так как все , оба фактора , и совокупный коэффициент корреляции являются значимыми (существенными).

б) Проверим значимость уравнения регрессии с помощью F – критерия Фишера по формуле (1.20). Предварительно определим остаточную дисперсию; для расчета числителя составим таблицу вспомогательных величин (табл.1.4).

Таблица 1.4

Вспомогательные величины для расчета

Порядковый номер рабочего
1	89,0	-3,0	9,0
2	91,2	-3,2	10,24
3	91,7	2,3	5,29
…	…	…	…
19	79,6	-2,6	6,76
20	88,7	3,3	10,89
Итого	---	---	177,2

и .

Для расчета определим число степеней свободы и . По табл. П2 Приложения 2 при уровне значимости = 0,05 находим, что . Поскольку (более чем в 14 раз), уравнение регрессии следует считать адекватным.

Таким образом, построенная регрессионная модель производительности труда пригодна для практического применения. Она может быть использована для выявления резервов повышения производительности труда.

7) Экономическая интерпретация регрессионной модели.

а) Проверим, согласуются ли знаки коэффициентов регрессии , c теоретическими предсказаниями о направлении влияния факторного признака на результативный признак.

Анализ коэффициентов регрессии позволяет сделать вывод, что

- с увеличением продолжительности внутрисменных простоев на 1 мин. следует ожидать снижения производительности труда (количества деталей, изготовленных одним рабочим за смену) в среднем на 0,41 шт. (обратная связь, это совпадает с выводом, сделанным в пункте 4а);

- повышение квалификации рабочего на один разряд может привести к возрастанию числа деталей, произведенных одним рабочим за смену, в среднем на 3,37 шт.

Данные выводы не противоречат логике.

б) Рассчитаем частные коэффициенты эластичности по формуле (1.21):

; .

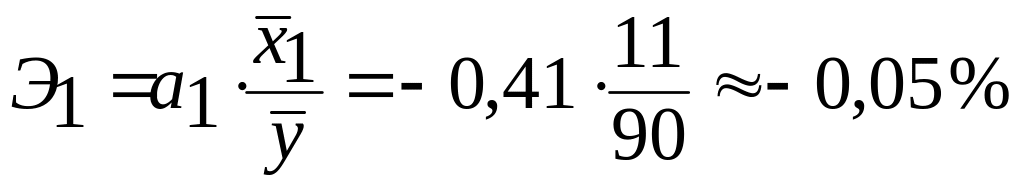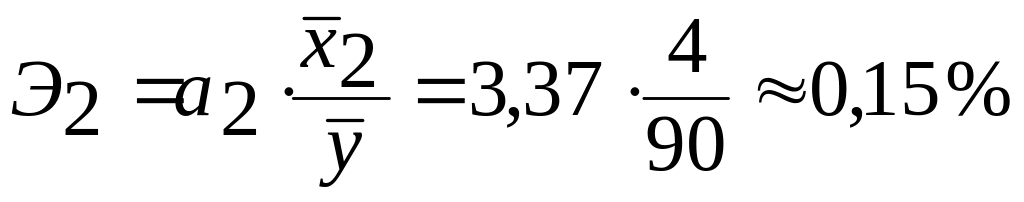Данные величины показывают, что по абсолютному приросту наибольшее влияние на производительность труда оказывает фактор - повышение квалификации рабочих на 1 % приводит к росту производительности труда на 0,15 %. Снижение продолжительности внутрисменных простоев на 1 % повышает производительность труда только на 0,05 %.

в) По формуле (1.22) определим значения β – коэффициентов:

; .

Анализ коэффициентов показывает, что на производительность труда наибольшее влияние из двух исследуемых факторов с учетом уровня их вариации способен оказать фактор - квалификация рабочих, так как ему соответствует наибольшее (по абсолютной величине) значение β – коэффициента.

г) По формуле (1.23) определим значения Δ – коэффициентов:

; .

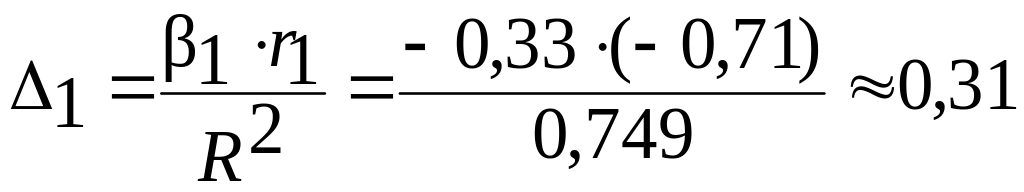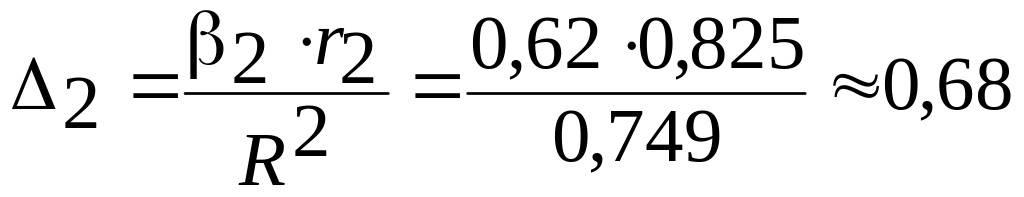Здесь , , .

На основании анализа Δ – коэффициентов установлено, что наибольшая доля прироста производительности труда из двух анализируемых факторов может быть обеспечена развитием такого фактора, как повышение квалификации рабочих.

Примечание: Для удобства расчета вспомогательных величин, используемых при определении основных показателей, рекомендуется все вычисления оформлять в табличном виде:

Таблица 1.5

К расчету параметров и оценке многофакторной регрессионной модели

№ п/п
1
2
…
n
Итого