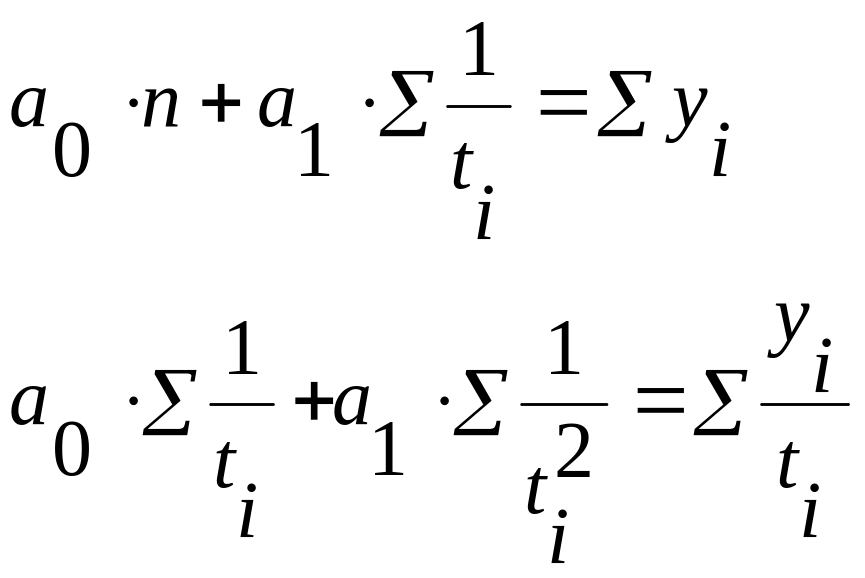3.2. Методика измерения параметров тренда

Когда тип тренда установлен, вычисляют оптимальные значения параметров тренда, исходя из фактических уровней. Для этого обычно используют метод наименьших квадратов (МНК). В этом методе минимизируется сумма квадратов отклонений фактических уровней динамического ряда от выровненных уровней (от тренда). Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую, рассчитывают параметры тренда. Однако вычислительный процесс определения параметров тренда при сохранении полной идентичности конечных результатов может быть упрощен, если ввести обозначения дат (периодов) таким образом, чтобы .

Если количество уровней в ряду динамики нечетное, то временные даты (t) обозначаются следующим образом (табл. 3.1):

Таблица 3.1

Временные даты (периоды)	2000	2001	2002	2003	2004
Уровни ряда динамики,
Обозначения временных дат, t	-2	-1	0	1	2

Если количество уровней в ряду динамики четное, то счет ведется полугодиями и обозначения временных дат (t) принимают следующий вид (табл. 3.2):

Таблица 3.2

Временные даты (периоды)	2000	2001	2002	2003	2004	2005
Уровни ряда динамики,
Обозначения временных дат, t	-5	-3	-1	1	3	5

В таблице 3.3 приводятся различные виды трендовых моделей и системы нормальных уравнений для определения параметров тренда.

3.3. Прогнозирование развития социально-экономических явлений на основе тренда

Аналитическое выравнивание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнить расчеты для периодов, для которых нет исходных данных.

Интерполяции - определение недостающих значений признака внутри рассматриваемого периода.

Экстраполяция - определение недостающих значений признака за пределами рассматриваемого периода.

Применение экстраполяции для прогнозирования основывается на предположении, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда. Это справедливо, если исследуемое явление развивается в достаточно стабильных условиях.

Таблица 3.3

Виды трендовых моделей

Наименование функции	Вид функции	Система нормальных уравнений для определения параметров тренда
Линейная
Полином 2–й степени (парабола)
Полином 3–й степени
Показательная
Гиперболическая

Так как анализируемые ряды динамики обычно относительно короткие, то и период экстраполяции не может быть бесконечным. Поэтому срок прогноза – период упреждения (период от конца базы расчета до прогнозируемого периода) не должен превышать длительности базы расчета тренда. На основе динамических рядов получают надежные прогнозы, если уровни ряда сопоставимы и получены по единой методологии.

В отличие от прогноза на основе регрессионного уравнения прогноз по тренду учитывает факторы развития только в неявном виде, что не позволяет «проигрывать» разные варианты прогнозов при разных возможных значениях факторов, влияющих на изучаемый признак. Однако прогноз по тренду охватывает все факторы, в то время как в регрессионную модель невозможно включить в явном виде более 10-20 факторов.

При составлении прогнозов уровней социально-экономических явлений рассчитывают доверительные интервалы прогноза, используя интервальную оценку. Границы интервалов определяют по формуле:

, (3.1)