Глава IV. Гетероструктуры

Рассмотренные в предыдущей главе p-n-переходы в современной электронике часто называют гомопереходами, т.е. переходами, созданными в процессе легирования разных частей одного и того же исходного полупроводника. Естественно, ширина основной запрещенной зоны во всех частях этого легированного полупроводника остается одинаковой. Однако в последнее время центр направлений исследований и разработок отчетливо смещается в сторону гетеропереходов, реализуемых в т.н. гетероструктурах. По мнению известного отечественного ученого - академика Ж.И.Алферова, лауреата Нобелевской премии по физике, гетероструктуры в XXI веке оставят гомопереходам в электронике только один процент.

4.1. Физические основы формирования гетероструктур

В общем случае, гетероструктуры можно определить как неоднородные полупроводниковые структуры, изготовленные из двух или более различных материалов (с различающимися ширинами запрещенных зон!!!) таким образом, что переходный слой (гетеропереход), т.е. граница раздела двух материалов играет важную роль в любом протекающем в приборе процессе. Можно даже сказать, что функциональным техническим устройством является сама граница раздела.

На рис. 4-1 приведена схема, иллюстрирующая случай, когда в контакт приведены два полупроводника с различными запрещенными зонами, а именно, GaAs (арсенид галлия) с шириной зоны 1,5 эВ и Al_xGa_1-xAs (арсенид алюминия-галлия), в котором часть атомов галлия замещена атомами алюминия. Заметим, что подобные образования часто называют твердым раствором. Величина х обычно изменяется от 0,15 до 0, 35 и соответственно растет ширина запрещенной зоны. В предельном случае х = 1 она достигает значения 2,2 эВ.

Рис. 4-1. Энергетические зоны на границе двух полупроводников. Е^с и Е^v – границы зоны

проводимости и валентной зоны, Е₃ – ширина запрещенной зоны.

Все материалы, из которых делаются гетероструктуры, относятся к центральной части Периодической системы элементов (таблице Менделеева). Ниже для наглядности приведена в упрощенной форме соответствующая часть таблицы, охватывающая нужные элементы II-VI групп.

Таблица

II	III	IV	V	VI
	Al	Si	P	S
Zn	Ga	Ge	As	Se
Cd	In		Sb	Te
Hg

В середине таблицы находится кремний – основа современной электроники. Он играет такую же важную роль в технологии электронных материалов, как и железо, точнее, сталь среди материалов конструкционных. Но, подобно тому, как современная металлургия занимается, кроме стали, и другими материалами, электроника, помимо кремния, имеет дело, например, с полупроводниковыми твердыми растворами. Так, каждый элемент III группы может вступать в соединение с любым элементом V группы. При этом возникают соединения этих групп – соединения типа А^IIIB^V. Наиболее часто используемое в технике соединение – арсенид галлия GaAs, однако любое из этих соединений может применяться в гетероструктурах – все зависит от конкретной цели. Фактически сегодня соединения А^IIIB^V используются, как правило, не в чистом виде, а в составе гетероструктур.

На рис. 4-1 показано, что для электронов, движущихся в узкозонном полупроводнике и имеющих энергию меньше Е^с₂ (пунктирная линия на рисунке), граница будет играть роль потенциального барьера. Легко понять, что два подобных гетероперехода ограничивают движение электрона в узкозонном полупроводнике с двух сторон, что эквивалентно образованию потенциальной ямы. Практически это достигается путем помещения тонкого слоя узкозонного полупроводника между двумя слоями материала с более широкой запрещенной зоной. В результате электрон оказывается запертым вдоль одного направления, что приводит к квантованию импульса и энергии в одном направлении, в то время, как в двух других движение электронов будет свободным. Поэтому можно считать, что электронный газ в квантовой яме становится двумерным.

Приведенный пример является примером т.н. гетеросистемы пониженной размерности. В общем случае, низкоразмерным, в отличие от объемного (3D, three-dimensional), называют такое состояние кристаллов, при котором движение носителей ограничено в одном, двух или всех трех измерениях. Соответственно, говорят о двумерных (2D), одномерных (1D) и нульмерных (0D) объектах. Обычно расстояния между эффективными границами измеряются десятками-сотнями нанометров, что позволяет ввести в рассмотрение т.н. квантовые ямы (2D), квантовые нити (1D) и квантовые точки (0D), где термин «квантовый» подчеркивает неизбежность возникновения квантово-размерных эффектов в указанных наноструктурах. Этим электроника с гетеропереходами принципиально отличается от вышерассмотренной электроники с гомопереходами, где, например, электронные энергетические уровни в пределах разрешенной зоны располагаются практически непрерывно (в силу макроскопических размеров полупроводникового 3D-кристалла).

4-2. Квантовые ямы

Как уже было продемонстрировано, одной из наиболее удачных пар для выращивания квантовых ям является полупроводник GaAs и твердый раствор Al_xGa_1-xAs. Чтобы вырастить квантовую яму, необходимо во время роста менять химический состав атомов, летящих на растущий слой. Сначала нужно вырастить слой полупроводника с широкой запрещенной зоной, т.е. Al_xGa_1-xAs, затем нанометровый слой узкозонного материала GaAs и, наконец, снова слой Al_xGa_1-xAs. Такая трехслойная структура иногда называется сэндвич. Энергетическая схема приготовленной таким образом квантовой ямы показана на рис. 4-2. Глубина ее – порядка нескольких десятых долей электронвольта. В такой яме разрешенными для электрона иногда оказываются только два энергетических уровня Е₁ и Е₂ , а волновые функции ψ на границе не обращаются в нуль (яма с конечной высотой стенок!).

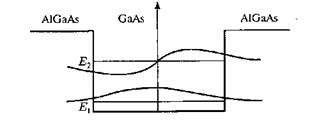
Рис. 4-2. Квантовая яма, сформированная в узкозонном полупроводнике

Реально, конечно, потенциальный барьер имеет более сложную форму, поскольку потенциал зависит и от межатомного расстояния, влияющего на волновые функции. Однако для многих случаев можно рассматривать потенциал, усредненный по нескольким межатомным расстояниям (т.н. приближение огибающей функции). Такой случай более подробно рассмотрен на рис. 4-3 и рис. 4-4, где отражены барьеры в квантовой яме и в зоне проводимости, и в валентной зоне. Теперь видно, что из-за наличия стенок ямы движение носителей (и электронов и дырок) не может происходить вдоль оси Z, перпендикулярной яме, однако в двух остальных направлениях (X иY, параллельных плоскости границы раздела) электроны остаются свободными, и их движение ничем не ограничено.

Рис. 4-2. Прямоугольная потенциальная яма в трехслойной системе.

Ось Z перпендикулярна границам слоев.

Поведение электронов в системах, где их движение абсолютно ограничено вдоль одной из координатных осей (в данном случае вдоль Z), приводит нас к известной квантово-механической задаче о движении частицы в так называемом потенциальном ящике с бесконечно высокими стенками и шириной a. Решение этой задачи для уравнения Шредингера с учетом граничных условий дает нам волновые функции и энергетические уровни связанных электронных состояний в виде

Ψ_n (z) = (2/a)^1/2 ∙ sin(πnz/a)

E_n = , где n = 1, 2, 3…

Из этих выражений видно, что квантовые эффекты должны особенно сильно проявляться в структурах с малыми значениями L, причем именно в материалах, где эффективная масса электрона является очень малой. Рассматриваемые нами наноструктуры GaAs очень удобны в этом отношении, т.к. в этом материале эффективная масса электрона m^* ~ 0,067 m_o (m_o – масса свободного электрона).

В соответствии с предложенным описанием движение электронов в квантовых ямах ограничено лишь в одном направлении Z, а в плоскости XY они остаются свободными и их поведение аналогично наблюдаемому поведению в трехмерных твердых телах. Поэтому представляется полезным записать волновую функцию электрона в виде произведения волновых функций по отдельным осям, т.е. представить ее в виде

Ψ = ψ_x∙ψ_y∙ψ_z

где в соответствии с используемой нами очень простой моделью функции ψ_x и ψ_y должны являться решениями уравнения Шредингера для свободного электрона. Т.е. описывать бегущую волну. Одновременно третья функция ψ_z должна представлять собой решение того же уравнения Шредингера, но для частицы в прямоугольной яме.

С учетом сказанного для полной энергии электронов в потенциальной яме можно выписать соотношение

E(k_x , k_y, n) = + E_n = + ,

где квазинепрерывные значения k_x и k_y должны определяться в соответствии с периодическими граничными условиями, как и в случае свободных электронов в объемном твердом теле.

У реальных квантовых ям энергетическая глубина конечна, что приводит к распределению волновой функции вдоль оси Z в виде, воспроизведенном на рис. 4-2. Тем не менее, все основные соотношения для Е применительно к относительно малым значениям n практически соответствуют решениям для бесконечно глубокой ямы. При этом особый интерес представляет то, что минимальная энергия электронов E₁ отлична от нуля. Для описываемых систем это значение называют нулевой энергией по аналогии с нулевой энергией квантового осциллятора.

Важное значение имеет вид функции плотности состояний g(E) для двухмерных структур, поскольку она определяет концентрацию электронов для каждого конкретного значения энергии. Ранее было показано на примере модели Зоммерфельда, что для трехмерных структур g(E) ~ E^1/2 . В двухмерном случае ситуация кардинально меняется. Следуя методу, использованному для трехмерной задачи, можно показать, что в двухмерных системах разрешенные значения k_x и k_y имеют периодичность 2π/L, где L – размер образца в плоскости XY, сечение которого без потери общности рассмотрения предполагается квадратным. Все это отражено на рис. 4-3. Число состояний в k-пространстве внутри кругового кольца, заключенного между k и k+dk, равно

а число состояний в k-пространстве на единицу координатной площади составляет

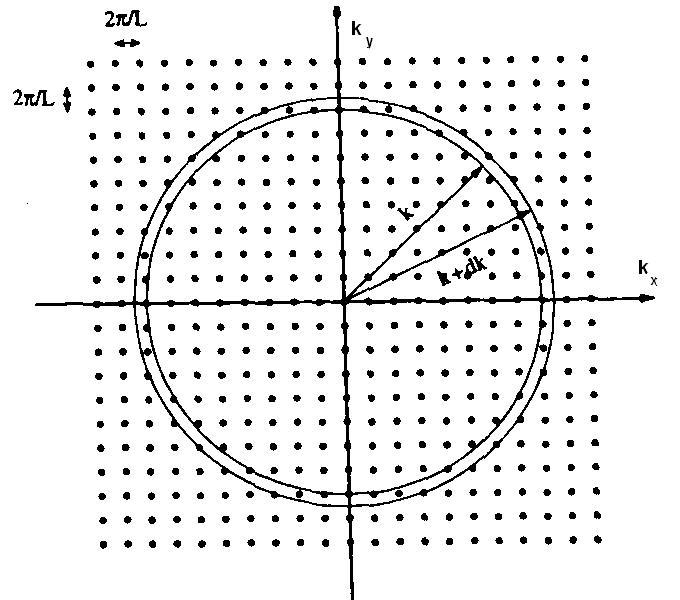
Рис. 4-3. Представление дискретных состояний для двухмерной электронной системы.

Если необходимо вычислить функцию плотности состояний по энергии в подзоне, то следует определить функцию g_2D(E) таким образом, чтобы величина g_2D(k)dk соответствовало числу состояний в диапазоне значений энергий dE. Другими словами, должно выполняться соотношение

g_2D(E)dE = g_2D(k)dk или g_2D(E) = g_2D(k)∙ ,

где величины E и k связаны формулой

E = (*)

Определяя из формулы (*) выражения для и вводя коэффициент 2 для учета спина электрона, получаем окончательно

Следует сразу отметить, что полученная для двухмерного случая функция плотности состояний является постоянной, т.е. не зависит от энергии в соответствующем поддиапазоне. Более того, эта функция является ступенчатой. Причем все ступени имеют одинаковую высоту, но располагаются на дискретных значениях E_n (определяемых свойствами квантовой ямы вдоль оси Z) , как это показано на рис. 4-4. Здесь же отражена пунктирной линией и огибающая, повторяющая аналогичную зависимость для трехмерного случая и демонстрирующая, что разница между двухмерным и трехмерными системами значительно сильнее проявляется при малых значениях n/

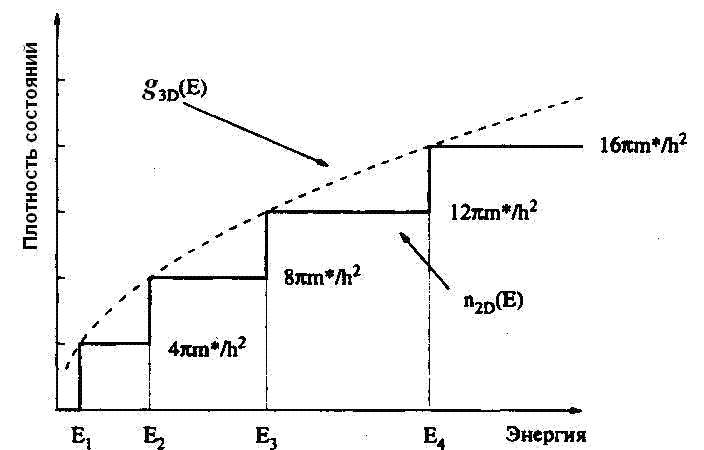
Рис. 4-4. Функции плотности состояний для двухмерной электронной системы.

В заключение этого раздела еще раз обсудим влияние конечности глубины потенциальных ям, которая должна совпадать со значением значения разрыва ΔЕ_с зоны проводимости на границе раздела сред GaAs и AlGaAs, которое для рассматриваемой задачи составляет несколько десятых эВ. Конечно, для практических целей удобнее воспользоваться полученным решением для ямы бесконечной глубины, только не надо рассматривать решения, относящиеся к очень высоким уровням энергии электронов.

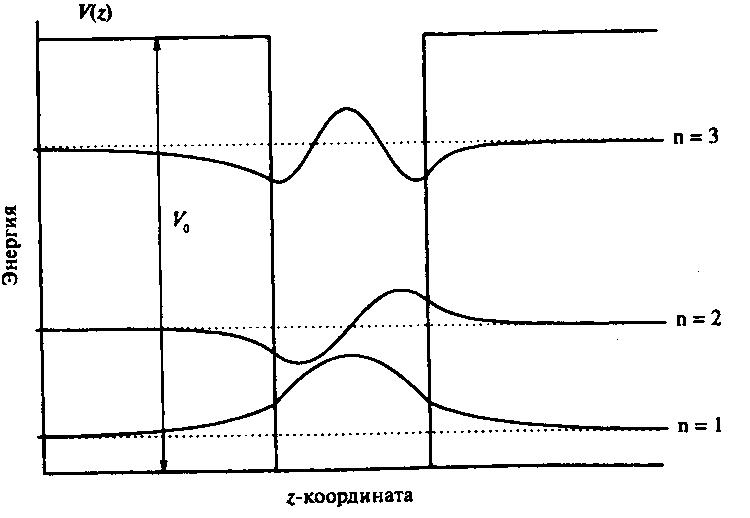
Рис. 4-5. Волновые функции и разрешенные энергетические уровни

для прямоугольной потенциальной ямы конечной глубины

Сказанное поясняет рис. 4-5. Здесь используется потенциальная яма глубиной V₀, причем подразумевается, что при энергиях E<V₀ мы имеем т.н. связанные состояния (т.е. электроны, захваченные или удерживаемые внутри ямы шириной a), а при E>V₀ мы имеем дело с непрерывными делокализованными состояниями, в которых электроны могут свободно двигаться вдоль оси Z. Аккуратное решение уравнения Шредингера в трех смежных областях и их «сшивка» дают вид первых трех волновых функций и разрешенных уровней энергии.

Анализ полученных решений еще раз показывает возможность проникновения связанных состояний в запрещенную зону. Это, конечно, чисто квантово-механический эффект.

4-3. Квантовые нити и точки

Вышеизложенное относительно квантовых ям позволяет понять (по крайней мере, в принципе) процесс создания квантовых нитей (проволок) и точек. Такие структуры можно сформировать на границе двух полупроводников, где уже находится двумерный электронный газ. С точки зрения физики, речь идет о создании дополнительных барьеров, ограничивающих движение электронов в двух (Z, X) и трех направления (Z, X, Y). Так, квантовые нити формируются в нижней точке V-образной канавки, образованной на полупроводниковой подложке. Если в основание этой канавки осадить полупроводник с меньшей шириной запрещенной зоны, то электроны этого полупроводника будут заперты в двух направлениях. Иногда такая квантовая нить определяется как одномерная структура.

Более изощренные технологии требуются для формирования квантовых точек (нульмерных структур). Тем не менее, к настоящему времени уже отработаны методики выращивания квантовых точек и их ансамблей в виде наноостровков (островков нанометровых размеров) предельно малых размеров (10-100 нм) с плотностью более 10¹⁰ – 10¹¹ см^-2. В квантовой точке движение ограничено в трех направлениях и электронный энергетический спектр полностью дискретный, как в атоме. Поэтому квантовые точки называют еще искусственными атомами, хотя каждая такая точка может содержать всего один или несколько свободных электронов. Если она содержит один такой электрон, то это как бы искусственный атом водорода, два – атом гелия и т.д. Это, в частности, стало поводом для появления представлений об атомоподобных характеристиках обсуждаемых здесь квантовых объектов. Например, низшее по энергии состояние электрона в нанокристалле соответствует s–состоянию электрона в атоме, а следующее – p-состоянию. Заполнение состояний двумя или шестью электронами в квантовой точке наиболее выгодно по энергии, что соответствует в атоме полностью заполненным электронным оболочкам.

Вернемся к определению плотности состояний g(E), но теперь для одномерного случая (квантовая нить). В одномерном фазовом пространстве (k, Y) эквивалентный «объем» элементарной ячейки равен (2π/L), где L – длина нити вдоль оси Y. Здесь использованы уже упоминавшиеся граничные условия Борна-Кармана, приводящие к условию kL = 2π∙n. Соответственно, элементарный «объем» в k-пространстве равен 2π, т.к. Δy = L.

Рис. 4-6. Элементарный объем в одномерном k-пространстве.

Из рис. 4-6 видно, что «объем» Δk в k-пространстве, приходящийся на интервал (k, k+dk), можно записать в виде Δk = 2∙dk. Тогда, с учетом принципа Паули, можно следующим образом определить плотность состояний g(E) в одномерном случае:

g(E)∙dE =

Отсюда, имея в виду соотношение E = ћ²k²/2m*, после несложных преобразований имеем:

g(E) =

Таким образом, плотность состояний в данном случае даже уменьшается с ростом энергии Е. На рис. 4-7 схематически показана зависимость плотность квантовых состояний от энергии для этой 1D-структуры.

Рис. 4-7. Зависимость плотности квантовых состояний от энергии в 1D-структуре.

Нульмерный электронный газ, как уже было сказано, реализуется в системах типа искусственного атома, когда ограничения на движение электрона распространяются на все три измерения. Спектр энергий в этом случае дискретен и подобен энергетическому спектру атома водорода. Условно функция плотности квантовых состояний в 0D-случае показана на рис. 4-8.

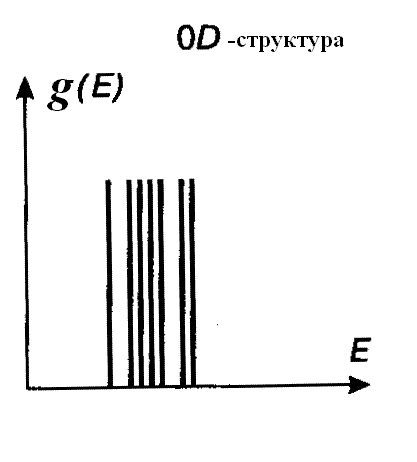
Рис. 4-8. Зависимость плотности квантовых состояний от энергии в 0D-структуре.