2.8. Контактные явления

2.9. Колебания решетки и акустические волны (фононный газ)

При всех своих достоинствах теории Зоммерфельда и Блоха предсказывают парадоксальный результат, а именно, что все металлы с идеальной кристаллической решеткой при нормальных условиях должны обладать свойством сверхпроводимости. Поскольку это совершенно не так, то ясно, что представленные теории не учитывают какие-то важнейшие взаимодействия. Анализ показывает, что все дело в постулировании неподвижности ионов или атомов в кристаллической решетке. Современный взгляд на проблему проводимости состоит в том, что атомы и ионы в узлах кристаллической решетки находятся в непрерывных колебаниях относительно равновесного положения, образуя распространяющиеся волны этих отклонений (т.н. акустические волны – фононы). Интенсивность этих колебаний и волн возрастает с температурой. В конечном итоге, сопротивление металлов определяется именно взаимодействием электронов с этими тепловыми колебаниями (в виде рассеяния электронов на флуктуациях электрических полей, создаваемых акустическими колебаниями). Снижение интенсивности колебаний с понижением температуры объясняет хорошо известный эффект понижения сопротивления металлов при уменьшении температуры проводника. Однако это сопротивление не снижается до нуля при Т = 0 из-за сохранения нулевых колебаний при этой температуре, а также вследствие наличия в кристаллической решетки металла различных дефектов. Вопрос сверхпроводимости, возникающий в некоторых металлах и сплавах при температуре около нуля, требует отдельного обсуждения, которое проведено в разделе 2.6..

Итак, колебания кристаллической решетки можно представить как совокупность упругих волн, распространяющихся в разные стороны, и которые можно рассматривать как газ особых квазичастиц - фононов. Такая картина фононного газа, заключенного в пределах образца кристалла, подобна известной из квантовой оптики ситуации, когда электромагнитное излучение можно представить как некий фотонный газ, заполняющий полость. Формально оба представления схожи – и фотоны, и фононы подчиняются одной и той же статистике, а именно, т.н. статистике бозонов (т.е. частиц с нулевым или целым спином). Эта статистика описывается распределением Бозе-Эйнштейна

где μ – химический потенциал (в пересчете на одну частицу), а f(E) указывает среднее число фононов с энергией , соответствующих данной волне (с частотой ω и определенной поляризацией).

Применив к фононному газу распределение Бозе-Эйнштейна, можно получить выражение для энергии колебаний кристаллической решетки, а, следовательно, и для теплоемкости кристаллов. Число фононов непостоянно (они могут возникать и исчезать), но их число определяется термодинамическими характеристиками системы, а не обменом с окружающей средой. Поэтому надо взять упомянутое распределение с условием равенства нулю химического потенциала μ (аналогично рассмотрению распределения по энергии фотонов в замкнутой полости).

Следует подчеркнуть, что в данном рассмотрении фононного газа слабо взаимодействующими считаются не атомы решетки (они как раз взаимодействуют очень сильно при взаимных перемещениях в ходе упругих колебаний), а собственно распространяющиеся упругие колебания. Отличие фононов от реальных частиц состоит, прежде всего, в том, что для существования и распространения таких квазичастиц нужна особая среда, в данном случае решетка кристалла.

Поскольку, как уже было сказано, атомы решетки связаны очень жестко, то они не могут осуществлять поступательного и вращательного движения: имеется только колебательное движение относительно неких центров равновесия в кристалле. Поэтому вся внутренняя энергия кристалла сосредоточена в энергии упругих колебаний атомов (как было показано выше в процессе изучении движения валентных, фактически свободных электронов в кристалле, они не вносят сколько-нибудь заметного вклада в теплоемкость в силу ряда квантовых эффектов).

Вычисление энергии кристалла, т.е. энергии фононного газа, в основном аналогично соответствующему вычислению энергии для фотонного газа. Но есть и отличия.

В твердом теле вдоль некоторого направления могут распространяться три разные волны с одним и тем же значением ω_i , различающиеся направлением поляризации: одна продольная волна и две поперечные с взаимно перпендикулярными направлениями колебаний. Поэтому соответствующий элемент фазового объема надо утраивать (а не удваивать, как для фотонов). Другими словами, g_i = 3. Кроме того, вместо скорости света с надо использовать скорость распространения упругих колебаний v в кристалле. С другой стороны, частота колебаний не может быть произвольно велика, как в случае фотонов. Это связано с тем, что длина волны не может быть меньше среднего расстояния между атомами в решетке, т.е. меньше чем n^-1/3, где n – концентрация атомов в кристалле. Поэтому максимальная частота нормальных колебаний кристаллической решетки зависит от ее параметров и равна, как показывает более точный анализ, ω_max = v . И, наконец, квантовомеханическое рассмотрение для упругого осциллятора (т.е. решение уравнение Шредингера с выражением для потенциальной энергии в виде U=kx²/2) дает следующее распределение всех возможных для осциллятора колебательных уровней энергии E_n = , где ω² = k/m, а значения n = 0, 1, 2,… Значит, в таком осцилляторе наименьшая энергия не равна нулю и даже при температуре абсолютного нуля существуют т.н. нулевые колебания (n = 0) с энергией E₀ = .

В результате проведения рассуждений и расчетов, аналогичных использованных для случая фотонов, и учитывая сделанные замечания по отличию фононов от фотонов, можно получить применительно к объему V следующую формулу для той части энергии фононных колебаний ΔU_i, которая соответствует интервалу частот Δω_i в окрестности ω_i

=

Полученное выражение отличается от известного выражения для фотонного газа лишь тем, что в нем имеется множитель 3/2 и вместо скорости света стоит скорость упругих волн v. Кроме того, учтен факт существования нулевых колебаний добавочным слагаемым ½ в квадратных скобках.

Суммирование предыдущего выражения по индексу i даст энергию кристалла. Однако математически удобнее заменить суммирование интегрированием (ввиду малости разности между энергетическими уровнями) и, выделяя отдельно полную энергию нулевых колебаний, можно в результате получит выражение для энергии в виде

Дифференцируя это выражение по температуре Т, а затем, разделив результат на объем кристалла, после ряда преобразований придем к довольно сложной формуле для теплоемкости единицы объема кристалла (т.н. удельной теплоемкости С)

Здесь n – концентрация атомов кристалла. Для общего анализа полученной формулы для теплоемкости удобно ввести величину Ө, определяемую условием = kӨ. Ее называют характеристической температурой Дебая. Температура Дебая указывает для каждого вещества ту область, где становится существенным квантование энергии колебаний.

Можно показать, что при T << Ө теплоемкость С окажется пропорциональной кубу температуры, т.е. С~T ³ . Эта приближенная зависимость известна как закон T ³ Дебая. При достаточно низких температурах этот закон выполняется во многих случаях очень хорошо. В частности, при приближении к абсолютному нулю температуры теплоемкость всех систем стремится к нулю.

При T >> Ө можно получить для внутренней энергии следующее приближение

что дает значение для удельной теплоемкости (теплоемкости единицы объема) C = 3nk. Если заменить концентрацию n на число Авогадро N_A, то получим известное классическое выражение для молярной теплоемкости C_m = 3R, составляющее суть закона Дюлонга и Пти. Статистическая физика показывает, что этот закон независимости молярной теплоемкости от температуры и ее одинаковости для всех веществ начинает асимптотически выполняться при достаточно высоких температурах. Например, для алюминия Ө = 396 К, а для меди Ө = 309 К.

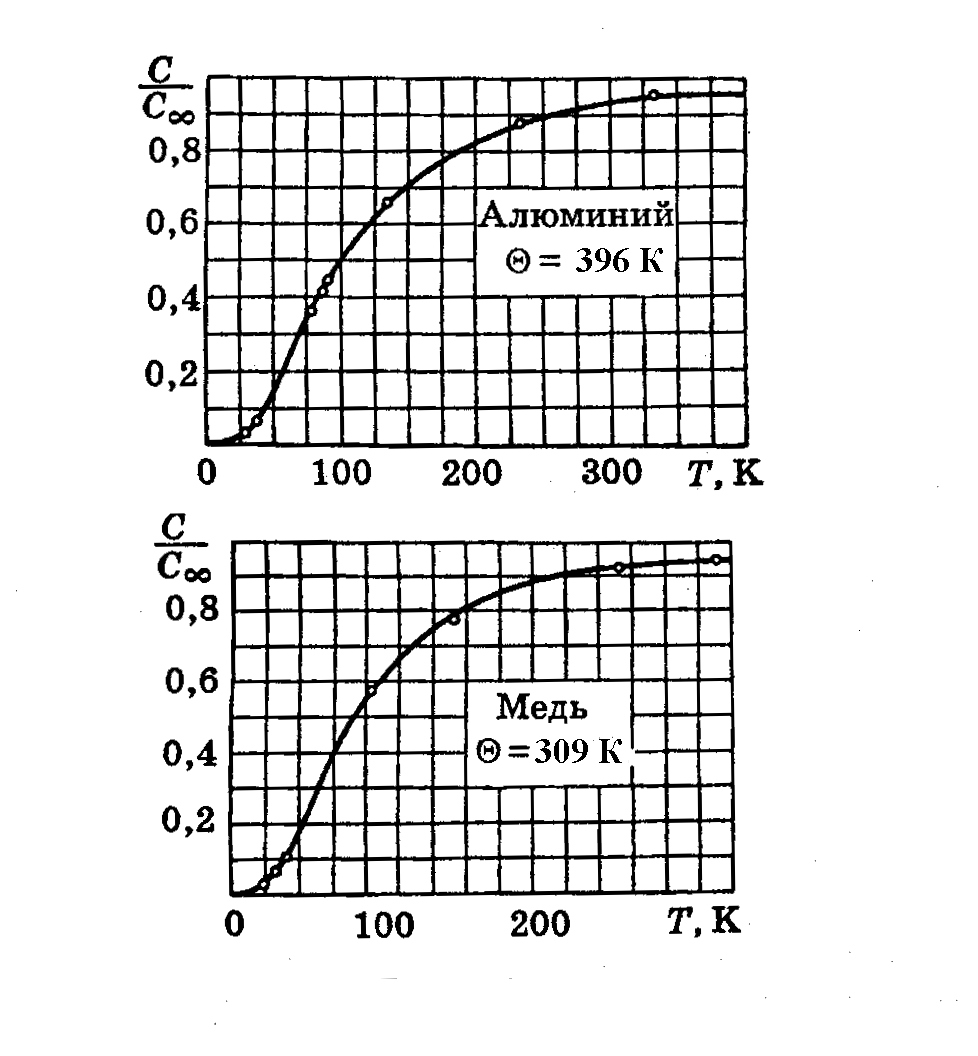
Рис. 2-16. Теплоемкость С по Дебаю - кривые на графиках как функция температуры.

Кружками показаны экспериментальные точки. С_∞ - классическое значение теплоемкости,

равное 3R для молярной теплоемкости.

На рис. 2-16 приведена экспериментальная зависимость теплоемкости металла от температуры, подтверждающая основные выводы теории Дебая.

Справедливости ради надо заметить, что формула Дебая хорошо передает ход теплоемкости с температурой лишь для тел с простыми кристаллическими решетками, т.е. для кристаллов из однородных химических элементов и для некоторых простых соединений. К телам с более сложной структурой формула Дебая неприменима, хотя качественно зависимость передается правильно, в. т.ч. в окрестности Т = 0. Наблюдаемые отличия от формулы Дебая связаны с гораздо более богатым спектром колебаний в сложных системах, где наряду с акустической ветвью появляется и оптическая ветвь колебаний (инфракрасного диапазона).

Еще раз отметим, что сопротивление металлов определяется именно взаимодействием электронов с этими тепловыми колебаниями в виде рассеяния электронов на флуктуациях электрических полей, создаваемых сложением акустических волн с различными частотами и поляризациями. Снижение интенсивности колебаний с понижением температуры объясняет хорошо известный эффект понижения сопротивления металлов при уменьшении температуры проводника. Однако это сопротивление не снижается до нуля даже при Т = 0 из-за сохранения нулевых колебаний при этой температуре, а также вследствие наличия в кристаллической решетки металла различных дефектов. Вопрос сверхпроводимости, возникающий в некоторых металлах и сплавах при температуре около нуля, требует отдельного обсуждения, проведенного в следующем разделе.