4. Оценка инвестиционных проектов с неординарными денежными потоками

В предыдущих разделах рассматривались стандартные, наиболее простые и ти­пичные ситуации, когда денежный поток представляется по вполне определенной схеме: инвестиция, или отток, капитала (со знаком в расчетах) и поступления, или приток, капитала (со знаком «+* в расчетах). Однако возможны неординарные ситуации, когда оттоки и притоки денежных средств чередуются. В частности, впол­не реальна ситуация, когда проект завершается оттоком капитала. Это может быть связано с необходимостью демонтажа оборудования, затратами на охрану окружаю­щей среды и др. В этом случае некоторые из рассмотренных аналитических показа­телей с изменением исходных параметров могут меняться в неожиданном направле­нии, т. е. выводы, сделанные на их основе, могут быть не всегда корректными.

Если вспомнить, что IRR является корнем (решением) уравнения NPV = О, а функция NPV = /(г) представляет собой алгебраическое уравнение k-ii степени, где k — число лет реализации проекта, то в зависимости от сочетания знаков и аб­солютных значений коэффициентов число положительных решений уравнения может колебаться от 0 до к., Иными словами, если значения денежного потока че­редуются по знаку, возможно несколько значений критерия IRR.

Рис. 17.6. Возможные графики NPV

Если рассмотреть график функции NPV = /(г, С¥_к), то возможно различное его представление в зависимости от значений ставки дисконтирования и знаков денежных потоков («+» или «-»). Можно выделить две принципиально различаю­щиеся ситуации (рис. 17.6).

Приведенные графики функции NPV = f(r,CF_k) соответствуют следующим ситуациям:

вариант 1 — имеет место первоначальное вложение капитала с последующими поступлениями денежных средств;

вариант 2 — имеет место первоначальное вложение капитала, в последующие годы притоки и оттоки капитала чередуются.

Первая ситуация наиболее типична: она показывает, что функция NPV = /(г) является убывающей с ростом ставки г и имеет единственное значение IRR. Во второй ситуации график может быть различным. В табл. 17.10 приведены вариан­ты инвестиционных проектов, соответствующие описанным ситуациям; графики функции у = NPV = /(г) приведены на рис. 17.7.

Таблица 17.10

Потоки с множественным значением IRR тыс. долл.)

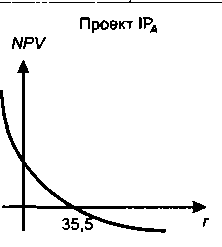
Рис. 17.7. Графики функции NPV = /(г) для проектов с различным числом IRR

С формальных позиций проект 1Рд имеет одно значение IRR, тогда как проек­ты 1Рд и IP_t- — соответственно 2 и 3. Отсюда возникает любопытная ситуация, ко­гда при изменении процентных ставок в экономике проект может меняться от приемлемого к неприемлемому. (Предлагаем читателю привести соответствующие примеры, в частности, в отношении проекта IPg.) Безусловно, приведенные ситуа­ции искусственны, а проекты с неординарными денежными потоками и имеющие несколько значений IRR оцениваются с помощью дополнительных критериев. Вновь повторим очевидную мысль, которой целесообразно придерживаться любо­му аналитику и менеджеру: формальные критерии не могут быть единственным и непреложным аргументом в принятии управленческих решений.

Выше отмечалось, что если в отношении NPV можно с определенной долей услов­ности сформулировать широко используемое в аналитической практике универсаль­ное правило «чем больше NPV, тем лучше», то ситуация с критерием 1RR несколько иная. Во многих случаях относительно большая величина IRR проекта является при­влекательной, однако это правило не является универсальным. Рассмотрим ситуацию.

Требуется дать заключения аналитического характера относительно проектов IP,i и IPs, имеющих следующие параметры.

Проекты имеют одинаковое значение IRR, однако выводы о значимости абсо­лютной величины IRR диаметрально противоположны. Так, проект IР^ приемлем при любом значении стоимости капитала, не превышающем IRR, т. е. в точности соответствует сформулированному ранее правилу; проект IPs приемлем только в случае, если стоимость альтернативного вложения средств превышает IRR, тогда NPV > 0, т. е. благосостояние акционеров при принятии проекта увеличится. Хотя проект 1Р_Л в большей степенн описывается классической схемой инвестирования (сначала вложение средств, потом отдача), проект IPs вовсе не является уникаль­ным. В качестве примера можно привести ситуацию, когда компания срочно нуж­дается в денежных средствах (например, для улучшения положения с ликвидно­стью) и потому принимает проект, генерирующий сиюминутные доходы, но тре­бующий определенных затрат в будущем.

С позиции денежного потока проекты 1Р_Л и IP_S принципиально разнятся, а одна из наиболее наглядных интерпретаций может быть такой: проект 1Р₄ опи­сывает предоставление в долг средств с последующим доходом по ставке 33,3% {<20 — 5): 15}, проект IPs — получение займа с последующими его погашением и выплатой процентов по ставке 33,3%. Естественно, что отношение субъекта, ини­циировавшего операцию (кредитора в первом случае и заемщика во втором), к этой ставке должно быть различным. Кредитор предпочитает как можно боль­шую ставку, т. е. в случае, описанном проектом IP.4, для него более привлекатель­ным является относительно большая ставка, являющаяся IRR проекта; заемщик — как можно меньшую, т. е. в случае, описанном проектом 1Ря, более привлекатель­ным уже становится меньшее значение IRR.

Действительно, для того чтобы вложить деньги в проект 1Р_Л, инвестор дол­жен изыскать источник, за который надо будет платить; поэтому чем выше [RR проекта IP,,, тем легче найти такой источник.

В проекте 1Рд заемщик получает средства, и чтобы вернуть их с требуемыми процентами, он должен вложить их так, чтобы по крайней мере не остаться в убытке. Поэтому чем ниже IRR проекта IPд, тем лучше для заемщика, поскольку легче найти приемлемые варианты инвестирования полученных средств. Графиче­ски описанная ситуация представлена на рис. 17.8.

Рис. 17.8. Иллюстрация логики ссудозаемных операций с помощью графика NPV

Проект IP.4 будет принят только в том случае, если стоимость источи и ка средств не превышает IRR = 333%; проект 1Рв — если доходность возможного вложения средств больше IRR.

Рассмотренная ситуация была относительно простой в том смысле, что проек­ты 1Р_А и IP в четко различались с позиции ссудозаемных операций, что давало ос­нование говорить о том, является ли относительно большее значение IRR привле­кательным. Безусловно, на практике не исключены и более сложные комбинации притоков и оттоков денежных средств, что делает невозможным принятие реше­ния лишь на основании критерия IRR-, приходится привлекать критерий NPV. Рас­смотрим следующую ситуацию.

Требуется провести анализ проектов IP_t- и I Р/>, имеющих следующие характе­ристики.

Эта ситуация отличается от предыдущей тем, что каждый из проектов пред­ставляет собой комбинацию действий по получению и предоставлению займа, а различие между ними состоит в противоположной последовательности этих операций.

Как упоминалось выше, каждый из потоков подобного типа может иметь не­сколько значений IRR, однако в данном случае лишь одно из них является дейст­вительным числом; иными словами, график NPV = /(г) пересекает ось абсцисс при положительных значениях г лишь однократно. Графики зеркальны по отно­шению друг к другу (рис. 17.9).

MPV

Различие состоит в том, что графики 1Р^ и 1Р_В имели одну точку пересечения с осью абсцисс, а графики IP с и IP д. т. е. с чередующимися знаками коэффициен­тов, могут иметь несколько таких точек, причем необязательно все они находятся на оси абсцисс справа от нуля.

Критерий IRR не делает различия между этими проектами и не позволяет принять решение, если, например, стоимость капитала равна 10%. Анализ графиков, т. е. привлечение критерия NPV, позволяет сделать точные оценки данной ситуации. Проект IPc может быть принят лишь в том случае, если альтернативные затраты капитала (или цена упущенных возможностей) не меньше 10%; напротив, проект 1Рв принимается при альтернативных затратах, меньших 10%. Таким образом, правило типа «чем больше, тем лучше» в отношении критерия IRR не срабатывает.

Могут быть ситуации, когда проект имеет несколько положительных значений IRR, однако оценка целесообразности принятия проекта возможна только с помощью критерия NPV. Рассмотрим проекты 1Р_Л и 1Рд, имеющие следующие характеристики.

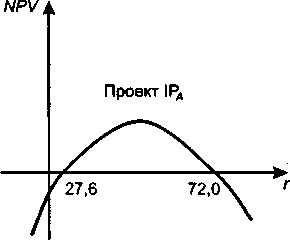
Рис. 17,10, Графики NPV с множественными положительными значениями IRR

Как видно из приведенных расчетов и графиков, представленных на рис. 17.10, выводы в отношении принятия проектов зависят от того, в какой ин­тервал попадает значение стоимости капитала. Так, проект IP.t приемлем лишь в том случае, если стоимость капитала меняется в интервале от 27,6% до 72%; на­против, проект 1Р_в выгоден лишь при сравнительно небольших либо при неогра­ниченно больших значениях стоимости капитала.

Не исключена и такая ситуация, когда анализируемый проект не имеет дейст­вительных значений IRR. Приходится пользоваться другими критериями. Рас­смотрим два примера.

Решение

С помощью критерия 1RR можно принять решение только в отношении про­екта 1Р„, а именно: в случае (а) проект можно включить в портфель; в случае (б) проект должен быть отвергнут. Что касается проекта IPt, то критерий IRR здесь бессилен, поскольку действительного значения IRR нет. Это можно видеть на гра­фике NPV (рис. 17.11).

Рис. 17.11. Графическое представление графиков NPV при наличии и отсутствии IRR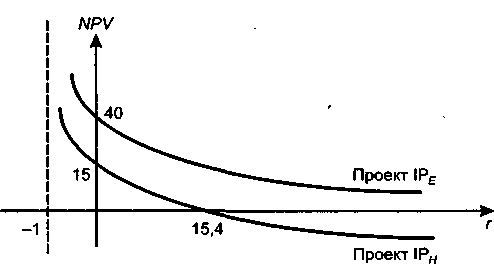

Как видно из рисунка и приведенных расчетов, график NPV плавно снижает­ся, приближаясь к оси абсцисс, но не пересекая ее на участке г > 0 Поскольку при любых значениях стоимости капитала NPV проекта IPf положителен, он мо­жет быть включен в инвестиционный портфель.

Пример 2

Имеются альтернативные проекты 1р£ и IPj с характеристиками, приведенными в таблице. Какой из них предпочтительней, если стоимость капитала: (а) 10%; (б) 60%?

Решение

Данная ситуация существенно отличается от предыдущей. Дело в том, что один проект был абсолютно предпочтительным. В данном случае графики NPV имеют точку пересечения, а значит, абсолютного приоритета одного проекта перед другим быть не может. Действительно, графики имеют следующий вид (рис. 17.12).

Рис. 17.12. Графики NPV при наличии точки Фишера и отсутствии IRR у одного из проектов

Может сложиться впечатление, что рассмотренные ситуации искусственны. Однако, во-первых, реальная жизнь вовсе не исчерпывается простейшими стан­дартными ситуациями и проекты с неординарными денежными потоками возмож­ны, особенно в ситуациях, когда по завершении проекта требуются некоторые ка­питаловложения, определяемые требованиями экологии. Во-вторых, этими приме­рами мы хотели продемонстрировать неоднозначность критерия IRR. В-третьих, примеры показывают, что в случае с неординарными денежными потоками крите­рий NPV явно предпочтительнее критерия IRR. С его помощью можно принять обоснованное решение по инвестиционному проекту.