1)Concept “information” term Information - is knowledge or information about anyone or anything. Information - is information that can be collected, stored, transmitted, processed, use it. From this point of view we can consider such information properties: memorability; transferability; reproducibility; blittable; abrasion. Systemology Working with the information associated with the transformation and always proves its material nature: record - the formation of the structure of matter and the flow through the modulation of interaction tool with a carrier; Storage - stability of the structure and modulation read (study) - the interaction of the probe the tool, the converter detector with the substrate or the flow of matter. Systemology considers the information through communication with other bases: I = S / F where: I - Information; S - systemic nature of the universe; F - functional communication; M - matter; ṿ - (v underlined) mark the grand unification (systemic, unity of reason); R - space; T - Time. Information - it does not matter and no energy, information - is information. "But the basic definition of the information that he gave to several of his books, the following: information - a designation the content that we have received from the external world in the process of adapting it to us and our feelings .
	2)Various approaches to information and their application measurement
	For convenience, in addition to apply bit larger units of information. 1bayt = 8 bits Byte - is an eight-digit binary code, with which you can submit a single character. When you type a character in a computer with a keyboard machine is transferred 1 byte of information. 1 KB (kilobyte) = 1024 bytes 1MB (megabyte) = 1024 KB 1GB (gigabyte) = 1024 MB 1TB (terabyte) = 1024 GB. In order to calculate the amount of information in the message, multiply the amount of information carried by one symbol, the number of characters. The information capacity of a single character is usually denoted by I, cardinality of the alphabet - N. These values ​​are related by the following formula: 2I = N, i.e. the information capacity of one character I = log2N. In this case, the amount of information in the same message must be determined separately for each recipient that is to have a subjective character. This is not to objectively evaluate the amount of information contained even in a simple statement. Therefore, when the information is treated as a novelty message to the recipient (consumer approach), there is no question about the measurement of the amount of information. 3)Information structural measures. Statistical approach. Entropy and its properties Structural measures only take into account the discrete structure of the information. The elements of the information center are quanta - indivisible piece of information. Distinguish geometric, combinatorial and additive measures. The definition of information geometrical method is to measure the length of the line, area or volume of a geometric model of the information system in the amount of quanta. The maximum number of photons in the given structural dimensions determines the information capacity of the system. Information capacity is a number indicating the number of photons in the full array of information. Statistical approach
	The probability p - a priori quantitative (ie, known prior to the experiment) characteristic of one of the outcomes (events) some experience. Measured in the range of from 0 to 1. If you know all the outcomes of the experiment, the sum of the probabilities is equal to 1, and the outcomes themselves constitute a complete group of events. If all outcomes can happen with equal probability, they are called equally likely. Entropy - the amount of information that is attributable to one elementary message source, generating statistically independent reports Entropy - a measure of the uncertainty of the experiment. properties . 4)Information units For your information, there are units of information. If we consider the communication of information as a sequence of characters, they can represent bits, and is measured in bytes, kilobytes, megabytes, gigabytes, terabytes and petabytes. The unit of measurement is the number of bits of information - is the smallest (elementary) unit. 1bit - is the amount of information contained in the message, which halves the uncertainty of knowledge about anything. Byte - a rather small unit of information. For example, one character - a 1-byte.  Derivatives unit for the amount of information 1 byte = 8 bits 1 kilobyte (KB) = 1024 bytes = 210 bytes 1 megabyte (MB) = 1024 Kilobytes = 210 kilobytes = 220 bytes 1 gigabyte (GB) = 1024 MB = 210 megabytes = 230 bytes 1 terabyte (GB) = 1024 gb
	5) Information transfer schemes Transmission of information - the physical process by which the movement of information in space. Information recorded on the disc and moved to another room. This process is characterized by the presence of the following components: Source of information. Receiver information. Media. The transmission medium. transmission of information - in advance organized a technical exercise, the result of which is reproduction of the information available in one place, provisionally called "source", in another place, conventionally called "the receiver of information." The event involves a predictable timeframe obtain the result

source of informations-- encoder transmitter (codes to signals)-- communication channels --converter(signal to codes) decoder recipient

6) Noise stability. Fidelity criterion.

Line noise immunity - the ability of the line to reduce the level of interference from the external environment and internal conductors. This ability depends entirely on:

characteristics of the process of the physical environment, line means intended for shielding and suppression of the line itself

The lowest is the figure of radio noise at a much greater resistance have cable lines and best - fiber-optic lines, insensitive to external electromagnetic radiation. Standard methods to reduce interference that appear due to external electromagnetic fields, are the methods of screening and / or twisting of the conductors.

With the known characteristics of the lines of communication are important methods for optimal reception of messages, which largely determine the accuracy and speed of information.

Taken to distinguish between three objectives:

Detecting messages when you want to install, whether the input data signal and the noise or just a hindrance. Detection of messages is done in asynchronous communication systems with passive pause.

The distinction between messages when you want to determine what message of the possible (known) messages sent. The distinction between messages is an important operation in synchronous communication systems with active pause.

Message recovery, which consists in the fact that on the basis of the received messages get distorted true for a given criterion.

Because the messages are transmitted using the signals solution of these problems depends on:

redundancy messages

encoding method

properties of the carrier signal,

types of modulation

channel interference characteristics,

demodulation method.

General analysis of all aspects of immunity is complex, so the solution is divided into separate stages. To do this, use the a priori information and consider the known characteristics of the type of signal and noise in the channel. Then the problem of noise analysis of message passing is determined primarily immunity reception.

In any case, noise estimation is based on transmission of messages selected (predetermined) evaluation criteria, i.e. some quantitative measure characterizing the quality of reception of information.

entropy is generally credited to Shannon

because it is the fundamental measure in information theory. Entropy is often defined as an expectation: H(X)= - E [log₂(P(X)] = -∑ P log₂ P

where 0 log(0) = 0. The base of the logarithm is generally 2. When this is the case, the units of entropy are bits.

1. Entropy is the amount of real and non-negative, since p_n probabilities in the range 0-1, the values ​​of log p_n always negative, and the value-p_n log p_n , respectively, are positive.

2. Entropy - the value of limited because for p_n-value log p_n also tends to zero, and for 0 <p_n<1 limited amount of all terms is obvious.

3. Entropy is equal to 0 if the probability of one of the states of the source of information is equal to 1, and thus the state of the source is fully determined (likely source of the remaining states are zero, since the sum of the probabilities must equal 1).

4. Maximum entropy with equal probabilities of all states sources of information

7) Conditional entropy.

N (αβ) = N (α.) H (β). This equation is called the rule of addition of entropy independent experiments.

If you waive the terms of the independence of the experiments α and β, then we will come to understand the conditional entropy.

Under these conditions, the entropy of a complex experience αβ will not equal the sum of the entropy of α and β. For example, if the experiment is consistent αβ retrieving balls from boxes containing only two colored ball. In this case, after the experience of α β experience will not contain any information entropy and sophisticated experience αβ is equal to the entropy of an experiment α, and not the sum of the entropy of α. and β.

The conditional entropy of β subject to the experience of α or the conditional entropy of experience α, subject to the experience of β is respectively N_α (β) and N_β (α):

N_α (β) = p (A₁) H_A1 (β) p + p (A₂) H_A2 (β) .... p (A_K) N_Ak (β),

where N_Ak (β) - the conditional entropy of β subject AK.

Thus, the formula for calculating the entropy H (αβ) complex experience α β, in the case of dependence experiments α and β, is given by

N (αβ) = N (α) Nα (β).

This expression is called the rule of addition of entropy for dependent experiments.

Properties of the conditional entropy

 

1. It is very important that the conditional entropy Nα (β) is between zero and the entropy H (β) (absolute): N (αβ) = N (α) + H (β)

  2. Given that the two challenging experience αβ and βα are not different from each other, H (αβ) = N (βα).

Nβ (α) = Ha (β) + {N (α)-H (β)}

8) The amount of information. Differential entropy

The amount of information - in information theory is the number of random data at one site relative to another. Let x-y random variables defined on the corresponding sets X and Y. Then the amount of information on there:

where ₂  - entropy and ₂  - conditional entropy in communication theory it characterizes the noise in the channel.

Properties of information

For the amount of information following properties hold:

  as a consequence of Bayes' theorem.

   if  and   –  if - the independent random variables.

The last property shows that the amount of information coincides with the entropy of information loss if the component (noise) is equal to zero.

Definition

Let X be a random variable with a probability density function f whose support is a set  . The differential entropy h(X) or h(f) is defined as

.

As with its discrete analog, the units of differential entropy depend on the base of the logarithm, which is usually 2 (i.e., the units are bits). See logarithmic units for logarithms taken in different bases. Related concepts such as joint, conditional differential entropy, and relative entropy are defined in a similar fashion.

One must take care in trying to apply properties of discrete entropy to differential entropy, since probability density functions can be greater than 1. For example, Uniform(0,1/2) has negativedifferential entropy

.

Thus, differential entropy does not share all properties of discrete entropy.

Note that the continuous mutual information I(X;Y) has the distinction of retaining its fundamental significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X and Y as these partitions become finer and finer. Thus it is invariant under non-linear homeomorphisms (continuous and uniquely invertible maps) ,^[1] including linear ^[2] transformations of X and Y, and still represents the amount of discrete information that can be transmitted over a channel that admits a continuous space of values.

9) Signal types

The analog signal (analog signal) is a continuous function of a continuous argument, ie is defined for any value of the argument. The sources of the analog signals are typically physical processes and phenomena that are continuous in the dynamics of its development in time, in space, or any other independent variable, and the detected signal is similar ("similar") is generated by its process.

Digital signal (discrete signal) in their values ​​as a continuous function, but only for certain discrete values ​​of the argument. For a variety of its meanings it is finite (countable) and describes a discrete sequence of samples (samples) y (n⌂t), where y₁<y<y₂, ⌂t - the interval between samples (range, or sample rate, sample time), n = 0, 1 , 2, ..., N.

Digital signal (digital signal) is quantized in their values ​​and discrete in the argument. It is described lattice quantized feature y_n = Q_k [y (n⌂t)], where Q_k - function with the number of quantization levels of the quantization k, wherein the quantization intervals may be either uniformly distributed, and the uneven, for example - a logarithmic. Sets of digital signals are usually in the form of a discrete number (discrete series) amounts.

10) Signal and its concept model 

The signal is a physical process that displays (carrying) the transmitted message, ie this variable physical quantity (current, voltage, electromagnetic field, light waves, etc.).

Distinguish primary and secondary signals. Primary electrical signals (PES) arise as a result of direct conversion of messages in an electromagnetic wave, usually at the output terminals. These include current variations microphone output current telegraph etc. Characteristic primary signal is a relatively low rate of change and, consequently, the possibility of low-frequency transmission channels, for example such as a wired network. It is sufficient for the transmission of speech channel transmits vibrations from 300 to 3400 Hz. When telegraph required bandwidth to a few hundred hertz.

11.Determined signal's various representation forms

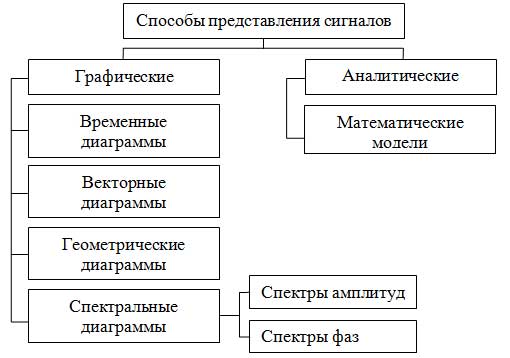
The timing diagram is a plot of any signal parameter (e.g., current or voltage) versus time (Figure 9). In the timing diagram can be observed signal waveform. Timing diagram (waveform) can be visually observed using a special measuring device - the oscilloscope. Vector diagram used in the study of the processes associated with changes in the signal phase (eg, phase modulation). In the diagram, the signal is a vector whose length is proportional to the amplitude signal and angle relative to the initial vector of signal indicates the phase signal is a geometric figure in the form of geometrical shapes. This chart can be used for visual representation of the signal.The spectral chart is a graph of the distribution of energy (amplitude spectrum) and the phase (phase spectrum) signal frequencies. More details on this method the signals to be described below. These diagrams can be seen using a special measuring device - a spectrum analyzer.Mathematical models of signalsThe mathematical model is a mathematical expression of a signal by which to determine the values ​​of the signal at any given time. ak - the constants of proportionality; k (t) - the elementary basis functions.hat is, a complex signal can be represented as the sum of elementary (simple) basis functions (signals), the amplitude of which will depend on the values ​​described by the signal.

12. Casual process,spectral signals representation

Consider the random process (t), having the expectation mu (t). Corresponding centered random process (t) is characterized at any point in time (t1) centered random quantity (t1): Centered random process (t) can expressed as a finite or infinite sum of orthogonal components, each of which represents a nonrandom basis function jk (t) with a coefficient Ck, is a random variable. As a result, we have the expansion centered random process (t): Random variables are called expansion coefficients Ck. In general, they are statistically independent, and this relationship is the matrix of correlation coefficients. The expectations of the expansion coefficients are zero. Nonrandom basis functions are called coordinate functions. canonical decomposition of the correlation function of a random process can be written of the canonical decomposition of a random process with the same coordinate functions, and dispersion coefficients of this expansion will be equal to the variances of the coefficients of expansion of the correlation function.

Thus, if the selected set of coordinate functions centered random process characterized by a set of dispersions of the expansion coefficients, which can be regarded as a generalized spectrum of a random process.

13.Signals sampling. Main methods

In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of asound wave (a continuous signal) to a sequence of samples (a discrete-time signal).A sample refers to a value or set of values at a point in time and/or space.A sampler is a subsystem or operation that extracts samples from a continuous signal.A theoretical ideal sampler produces samples equivalent to the instantaneous value of the continuous signal at the desired points. Sampling can be done for functions varying in space, time, or any other dimension, and similar results are obtained in two or more dimensions. Audio sampling.Digital audio uses pulse-code modulation and digital signals for sound reproduction. This includes analog-to-digital conversion (ADC), digital-to-analog conversion (DAC), storage, and transmission. In effect, the system commonly referred to as digital is in fact a discrete-time, discrete-level analog of a previous electrical analog. While modern systems can be quite subtle in their methods, the primary usefulness of a digital system is the ability to store, retrieve and transmit signals without any loss of quality. Video sampling Standard-definition television (SDTV) uses either 720 by 480 pixels (US NTSC 525-line) or 704 by 576 pixels (UK PAL 625-line) for the visible picture area.High-definition television (HDTV) is currently moving towards three standards referred to as 720p (progressive), 1080i (interlaced) and 1080p (progressive, also known as Full-HD) which all 'HD-Ready' sets will be able to display. Undersampling When one samples a bandpass signal at a rate lower than the Nyquist rate, the samples are equal to samples of a low-frequency alias of the high-frequency signal; the original signal will still be uniquely represented and recoverable if the spectrum of its alias does not cross over half the sampling rate. Such undersampling is also known as bandpass sampling, harmonic sampling, IF sampling, and direct IF to digital conversion Oversampling is used in most modern analog-to-digital converters to reduce the distortion introduced by practical digital-to-analog converters, such as a zero-order hold instead of idealizations like the Whittaker–Shannon interpolation formula. Complex sampling refers to the simultaneous sampling of two different, but related, waveforms, resulting in pairs of samples that are subsequently treated as complex numbers.

14. Signal's restoration mistakes  Information technology is based on abstraction of messages with the bits 0 and 1. In fact, the entities running through the internet and PCs are electric and photonic pulses each representing 0 and 1. This representation allows one to realize efficient data compression and reliable transmission under noises. This is coding, and consists mainly of source coding which concerns effective representation (compression) of messages with 0 and 1, and channel coding which is about how to transmit bit sequences with the minimum error. Alphabets from the information source (ρ1, ρ2, ρ3, ...) are first converted into bit sequences by the source encoder so as to compress original messages into smaller bits. Essentially, source coding entails representation of common alphabet in a message as short sequences of bits, and uncommon alphabet as longer sequences, to make the average length of the coded message as short as possible. The unequal frequencies of the letters imply a redundancy that enables the compression of the message. The outputs from the source encoder are further encoded by the channel encoder into appropriate code words by adding some redundant bits to protect information from noise disturbances in the channel. An output from the channel is generally different from an input code word due to noise. Then at the receiving side, we try to decode the original signal by applying appropriate error correction. Finally we decompress the decoded signal to restore the original messages. 

 Shannon established information theory by quantifying the effectiveness and the limits of these codings in 1948. Shannon's information theory is a quite mathematical and hence very general theory. Unfortunately, however, Shannon's information theory is not perfect modeling of physics behind information. Information theory should eventually be represented by the words of quantum mechanics. It is quite recently, after 90's, when such representations are clarified.

15 V.A.Kotelnikov theorem and its applicability

V.A.Kotelnikov theorem - if the analog signal has a finite (limited by width) spectrum, then it can be recovered uniquely and without loss in their readings, taken at a rate strictly greater than twice the upper frequency:

This interpretation considers the ideal case, when the signal started infinitely long time and will never end, and does not have the time characteristic points of discontinuity. That means it is the concept of "range, limited frequency."

Of course, the actual signals (e.g., audio on digital storage media), do not have such properties as they are finite in time and usually have a time lag characteristic. Accordingly, their range is endless. In this case, a full recovery is not possible and the signal from the Kotelnikov theorem two corollaries:

Any analog signal can be reconstructed with whatever precision from its discrete samples taken at the frequency where   , где   — - the maximum frequency range which is limited by the actual signal.

If the maximum signal frequency exceeds half the sampling frequency, the process to recover the signal from analog to digital there is no distortion.

Broadly speaking, Kotelnikov theorem states that a continuous   signal can be represented in the form of interpolation series

where - the function sinc   . The sampling interval satisfies the constraints of the instantaneous values ​​of the series is a discrete signal samples ..

16 Signals quantization

Signals quantization - sampling the continuous signal, converting the electrical signal continuously in time and level to a sequence of discrete (separate), continuous or discrete signals, which reflect the original signal combined with a predetermined error. K. s. data transmission is performed in the remote control system, analog-to-digital conversion in the computing technique in pulse automation systems, etc.

When sending continuous signals typically not sufficient to transmit the signal itself, but rather the sequence of its instantaneous values ​​of the selected signal source to a specific law. K. s. performed in time, the level, or both parameters simultaneously. When K s. a time signal at regular intervals interrupted M (pulse signal) or changes abruptly.

For example, a continuous signal passing through the contacts periodically include electrical relays, is transformed into a sequence of pulsed signals. With infinitely small intervals on (off), ie, at infinite frequency switching contacts is an accurate representation of a continuous signal. When K s. the level corresponding to the instantaneous values ​​of the continuous signal are replaced by the nearest discrete energy levels that form a discrete quantization scale. Any signal value is between the levels, rounded to the nearest level.

17. Signal's transfer process errors assessment

18 Signal modulation types

Modulation - the process of changing some parameters of the carrier signal under the influence of the information flow. This term is commonly used for analog signals. With respect to digital signals, there is another term "manipulation," but it is often replaced by the same word "modulation" implying that it is a digital signal.

There are 3 main types of manipulation of signals:

amplitude (Amplitude-shift keying (ASK)), frequency (Frequency-shift keying (FSK)) and phase (Phase-shift keying (PSK)). This set is determined by the manipulation of the basic characteristics possessed by any signal (see "signal and its characteristics").

Phase shift keying (FM)

Phase Shift Keying (English Phase-shift keying (PSK)) involves the phase change of the carrier signal depending on the transmitted symbol. To transmit a "0", for example, may be used an initial phase of 0 degrees, and for "1" - 180 degrees. This kind of manipulation is more complex to implement, but at the same time the most resistant to interference of the three. One of the major drawbacks of PSK is the effect of "reverse operation" in the phase detector (a device that stands out from the manipulated signal information) when the error in one symbol may lead to an erroneous detection of all subsequent characters.

Amplitude Modulation (AM)

Amplitude Modulation (born Amplitude-shift keying (ASK)) - this is one of the most common types of digital modulation signals. Keying means for transmitting that "0" and "1" levels use different carrier signal voltage. For example, the transmission of "0" corresponds to 5B, a "1" - 1V. The frequency and phase of the carrier signal remains constant. To improve noise levels are often used with different polarity (e.g., "0": 5B, a "1":-5V). This is the simplest of all kinds of manipulation. Arrangements for the implementation of keying are also easy and inexpensive. In addition, amplitude modulation requires minimum bandwidth communication channel.

In frequency shift keying based on the transmitted symbol frequency of the carrier signal is changed. For example, for transmission "0" frequency of 5 Hz is used, and "1" - 10Hz. This kind of manipulation is also not difficult to implement and is less prone to interference than amplitude modulation. But, on the radio quite often observed frequency-selective interference caused by operation of industrial equipment (generators, transformers). If the transmitted signal will be in the band of the actions of such interference is possible that a high percentage of data loss or even complete "overlap" link.