
- •Номер столбца соответствует стратегии , применяемой игроком номер строки соответствует номеру стратегии , применяемой игроком
- •Игрок стремится минимизировать свой проигрыш и выбирает стратегию, соответствующую минимальному проигрышу: .
- •Приведение матричной игры к задаче линейного программирования (злп).
- •Задачи теории статистических решений (тср).
- •Множество состояний природы - , отдельное состояние - . Множество решений (стратегий) статистика - , отдельное решение - .
- •Игра 2-х участников с нулевой суммой.
Термин игра означает совокупность предварительно оговоренных правил и условий (партия - частичная возможная реализация этих правил). Математически, конфликтная ситуация – это игра, в которой каждый из игроков, стремится максимизировать свой выигрыш за счет других игроков. Совокупность правил, однозначно определяющих последовательность действий стороны в конкретной конфликтной ситуации, называется стратегией.
Теория
игр
- раздел математики, занимающейся
выработкой оптимальных правил поведения
для каждой из сторон, участвующей в
конфликтной ситуации. Если в игре
участвуют
 игроков
игроков
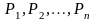 ,
то изучается проблема: как должен вести
партию
,
то изучается проблема: как должен вести
партию
 -й
партнер
-й
партнер
 для достижения наиболее благоприятного
исхода.
для достижения наиболее благоприятного
исхода.
Классификация игр
|
||
по числу игроков |
игры, в которых участвуют два игрока - парные, с большим числом игроков – множественные |
|
по способу выбора решения |
принятие игроком того или иного решения и его реализация - ход (ходы могут быть случайными если ход выбирается с помощью механизма случайного выбора и личными, если выбор сознательный) |
|
по количеству стратегий |
игры делятся на конечные и бесконечные |
|
по возможности образовывать коалиции |
если игроки не имеют право вступать в соглашения, то игра - бескоалиционная, если могут создавать коалиции - коалиционная; в кооперативной игре коалиции определены заранее |
|
в зависимости от вида функции выигрышей |
игры подразделяются на матричные, биматричными, непрерывные, выпуклые, сепарабельные |
|
по
окончании партии игрок
|
числа
|
в
играх
с нулевой суммой:
|
|
||
при
|
||
М
каждый
элемент
 - действительное число, представляющее
собой сумму выигрыша, уплачиваемую
игроком
- действительное число, представляющее
собой сумму выигрыша, уплачиваемую
игроком
 игроку
игроку
 ,
если
выбирает стратегию, соответствующую
,
если
выбирает стратегию, соответствующую
 -й
строке, а
выбирает стратегию, соответствующую
-му
столбцу
-й
строке, а
выбирает стратегию, соответствующую
-му
столбцу
атричная игра однозначно определяется прямоугольной матрицей размерности
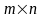 :
:





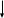
Номер столбца соответствует стратегии , применяемой игроком номер строки соответствует номеру стратегии , применяемой игроком
Первый игрок стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, второй игрок выбирает стратегию, приводящую его к минимальному проигрышу.
Чистая
стратегия
 первого игрока (чистая стратегия
первого игрока (чистая стратегия
 второго игрока) – это возможный ход
первого (второго) игрока, выбранный им
с вероятностью равной единице. Чистые
стратегии можно представить в виде
единичных векторов:
второго игрока) – это возможный ход
первого (второго) игрока, выбранный им
с вероятностью равной единице. Чистые
стратегии можно представить в виде
единичных векторов:
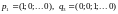 .
.
Нижняя
чистая цена игры
(максимин) - число
 :
:
 .
.
Верхняя
чистая цены игры
(минимакс) -
 :
:
 .
.
Максимин
не превосходит минимакс:
 .
.
Если
для чистых стратегий
 игроков
игроков
 и
и
 верно равенство
верно равенство
 ,
пара чистых стратегий
,
пара чистых стратегий
 - седловая
точка
матричной игры,
элемент
–
седловой
элемент платежной матрицы,
число
- седловая
точка
матричной игры,
элемент
–
седловой
элемент платежной матрицы,
число
 - чистая
цена игры.
- чистая
цена игры.
П
какой бы выбор по столбам ни сделал игрок , выигрыш игрока , который свои стратегии выбирает по строкам, в худшем случае составит, соответственно: -3, 3, 1, 2
ример 1:

игроку целесообразно выбрать такую стратегию (строку), для которой достигается максимальный выигрыш независимо от того, какой столбец выбрал игрок :



игрок выбирает стратегии по столбцам, поэтому какие бы стратегии ни выбрал игрок , в худшем случае игрок может проиграть: 5, 7, 8, 9.
Игрок стремится минимизировать свой проигрыш и выбирает стратегию, соответствующую минимальному проигрышу: .
Максиминная
стратегия игрока
-
 ,
минимаксная стратегия игрока
-
,
минимаксная стратегия игрока
-
 .
.
П
 седловая
точка
седловая
точка
ример 2.
5

1
-4


9 5 6 8

Если
матричная игра не имеет седловой точки,
то
 и решение находят в смешанных стратегиях.
Смешанной
стратегией
называются вектор
и решение находят в смешанных стратегиях.
Смешанной
стратегией
называются вектор
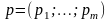 ,
где
,
где
 и
и
 или вектор
или вектор
 ,
где
,
где
 и
и
 .
В смешанных стратегиях любая конечная
матричная игра имеет седловую точку.
.
В смешанных стратегиях любая конечная
матричная игра имеет седловую точку.
Вектор
 означает вероятность применения
-й
чистой стратегии первым игроком (
-й
чистой стратегии вторым игроком). Игроки
выбирают свои чистые стратегии случайно
и независимо друг от друга, поэтому игра
имеет случайный характер и величина
выигрыша (проигрыша) - случайна;
математическое ожидание выигрыша
(проигрыша) - функция от смешанных
стратегий
означает вероятность применения
-й
чистой стратегии первым игроком (
-й
чистой стратегии вторым игроком). Игроки
выбирают свои чистые стратегии случайно
и независимо друг от друга, поэтому игра
имеет случайный характер и величина
выигрыша (проигрыша) - случайна;
математическое ожидание выигрыша
(проигрыша) - функция от смешанных
стратегий
 (
(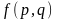 - платежная функция игры
- платежная функция игры
 ):
):
 .
.
Стратегии
 - оптимальные,
если для произвольных стратегий
,
выполняется условие:
- оптимальные,
если для произвольных стратегий
,
выполняется условие:
 .
.
Смешанные
стратегии
оптимальны в игре с матрицей
и выигрышем
 ,
если:
,
если:
 .
.
Совокупность
оптимальных стратегий и цены игры -
решение
игры; цена
игры
равна:
 .
.
Использование
в игре оптимальных смешанных стратегий
обеспечивает первому игроку выигрыш,
не меньший, чем при использовании им
любой другой стратегии
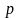 ;
второму игроку – проигрыш, не больший,
чем при использовании им любой другой
стратегии
;
второму игроку – проигрыш, не больший,
чем при использовании им любой другой
стратегии
 .
Если игрок
применяет оптимальную смешанную
стратегию
.
Если игрок
применяет оптимальную смешанную
стратегию
 ,
а игрок
-
любую чистую стратегию
,
то выигрыш игрока
будет
не меньше цены игры
.
Если игрок
использует оптимальную смешанную
стратегию
,
а игрок
-
любую чистую стратегию
,
то выигрыш игрока
будет
не меньше цены игры
.
Если игрок
использует оптимальную смешанную
стратегию
 ,
а игрок
любую чистую стратегию
,
то проигрыш игрока
не превысит цены игры
.
,
а игрок
любую чистую стратегию
,
то проигрыш игрока
не превысит цены игры
.
Чистые стратегии игрока, входящие в его оптимальную смешанную стратегию с вероятностями, отличными от нуля, называют активными стратегиями игрока. Если один из игроков придерживается своей оптимальной стратегии, то его выигрыш равен цене игры независимо от того, какую стратегию применяет другой игрок, если только тот не выходит за пределы своих активных стратегий.
Решение
игры можно упростить, выявив доминирование
одних стратегий над другими. Рассматривая
стратегии игрока
,
сравнивают элементы строк
 и
и
 :
:
 с
с
 для
для
 ;
если
;
если
 ,
то выигрыш игрока
при стратегии
,
то выигрыш игрока
при стратегии
 будет
больше, чем при стратегии
будет
больше, чем при стратегии
 (стратегия
- доминирующая,
-
доминируемая).
(стратегия
- доминирующая,
-
доминируемая).
Игрок
заинтересован в минимизации проигрыша,
поэтому доминирующим будет столбец с
наименьшими элементами. Сравнивают
элементы
 -го
и
-го
и
 -го
столбцов: если все элементы
-го
столбцов: если все элементы
 ,
то игроку
выгоднее сделать выбор по
-му
столбцу, стратегия
,
то игроку
выгоднее сделать выбор по
-му
столбцу, стратегия
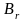 доминирует над стратегией
доминирует над стратегией
 .
.
В матричной игре доминируемые и дублирующие строки (столбцы) можно опускать, что не влияет на решение игры.
Оптимальные
смешенные стратегии
и
соответственно игроков
и
в матричной игре
с выигрышем
будут
оптимальными и в матричной игре
 с выигрышем
с выигрышем
 ,
где
,
где
 .
.
П

 ример.
Выполнить все возможные упрощения
матричной игры:
ример.
Выполнить все возможные упрощения
матричной игры:



 .
.


Упрощенная
матрица: 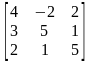 .
.
Чтобы получить матрицу с положительными элементами достаточно прибавить к её элементам, например, 2:
 .
.

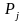 получает сумму
получает сумму
 -
выигрыш
-
выигрыш ,
соответствуют выигрышу игрока
,
соответствуют выигрышу игрока сумма выигрыша переходит от одного
игрока к другому, не поступая из внешних
источников; сумма выигрышей всех
игроков в каждой партии равна нулю
сумма выигрыша переходит от одного
игрока к другому, не поступая из внешних
источников; сумма выигрышей всех
игроков в каждой партии равна нулю проигрышу
игрока
проигрышу
игрока реализуется ничейный исход
реализуется ничейный исход