
I часть
Первое - вероятность есть фактор,
оперирующий в сфере естественных сил.
Второе – вероятность не оперирует как фактор.
Вывод – мы во власти не- , противо- или
сверхъестественных сил.
Том Стоппард «Розенкранц и Гильденстерн мертвы».
Сидоров, о Сидоров, что бы я без тебя делала…
Грустила бы, наверное, как обычно…
Живи долго Сидоров, и, по возможности, счастливо.
Автор(ша)
09.01.2010.
Теорией
вероятностей
называется раздел высшей математики,
изучающий закономерности, присущие
случайным событиям и процессам.
«Закономерность случайности» звучит
парадоксально, но ничего противоречащего
здравому смыслу в этом словосочетании
нет, и человека размышляющего оно не
отпугивает, например, Том Стоппард в
пьесе «Розенкранц и Гильденстерн мертвы»
пишет, что «случайность и упорядоченность
образуют некий союз, в котором мы узнаём
природу» .
Разумеется, исход одного случайного
эксперимента предсказать невозможно,
но если производятся множественные
испытания, начинают проявляться законы
природы в виде математических
закономерностей.
.
Разумеется, исход одного случайного
эксперимента предсказать невозможно,
но если производятся множественные
испытания, начинают проявляться законы
природы в виде математических
закономерностей.
Основное базовое понятие теории вероятностей – случайный эксперимент, то есть эксперимент, который можно повторить сколь угодно много раз при воссоздании одного и того же комплекса начальных условий, причём исход каждого отдельного испытания случаен. Примером случайного эксперимента является многократное подбрасывание «правильной» монеты (т.е. монеты с несмещённым центром тяжести). Лучше всего это проделывать при помощи специального механизма, чтобы исключить действие индивидуальности экспериментатора (его усталость, раздражение, заинтересованность и т.п.). Вместо термина эксперимент допустимо употребление слов наблюдение, опыт, испытание.
В
результате отдельного испытания могут
реализоваться сложные и элементарные
исходы. Их легко различить: элементарные
(простейшие, не имеющие внутренней
структуры) исходы нельзя разложить на
составные части, а сложные исходы
составлены из элементарных. Например,
один раз выбрасывается правильная
игральная кость. Элементарным исходом
является «выпадение 3», а сложным –
«выпадение нечётного числа», потому
что этот исход включает в себя выпадение
единицы, тройки или пятёрки. Все
элементарные исходы случайного
эксперимента образуют множество
элементарных исходов,
обозначаемое буквой
 (омега).
В примере с однократным выбрасыванием
игральной кости
(омега).
В примере с однократным выбрасыванием
игральной кости
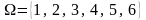 .
Это конечное, дискретное множество и
его можно задать перечислением входящих
в него элементов. Но в прикладных задачах
могут встречаться множества элементарных
исходов с другими характеристиками
(непрерывные, дискретно-непрерывные,
бесконечные и.т.д.).
.
Это конечное, дискретное множество и
его можно задать перечислением входящих
в него элементов. Но в прикладных задачах
могут встречаться множества элементарных
исходов с другими характеристиками
(непрерывные, дискретно-непрерывные,
бесконечные и.т.д.).
Любое
подмножество множества элементарных
исходов называется случайным
событием.
Обычно случайные события обозначаются
большими латинскими буквами, и указывается
множество элементарных исходов, которые
соответствуют этому событию. Например,
если при однократном выбрасывании
игральной кости выпадает нечётное
число, говорят, что произошло событие
 ,
причём
,
причём
 .
.
Событие,
которое в результате проведённого
испытания обязательно произойдёт,
называется достоверным.
Множество исходов, соответствующих
этому событию совпадает с
.
Например,
если один раз подбросить правильную
игральную кость, то выпадение положительного
числа будет достоверным событием.
Событие, которое не может наступить в
результате проведённого испытания,
называется невозможным,
и ему соответствует множество исходов,
называемое пустым
 .
Невозможно выпадение 7, при однократном
выбрасывании игральной кости.
.
Невозможно выпадение 7, при однократном
выбрасывании игральной кости.
Событие
влечёт
за собой
событие
 ,
если
,
если
 (при каждом наступлении события
,
наступает и событие
)
(рис.1).
(при каждом наступлении события
,
наступает и событие
)
(рис.1).
Например,
если один раз подбросить правильную
игральную кость, то выпадение тройки
влечёт за собой наступление события
|
|
Рисунок 1. Событие влечёт за собой событие : если |
События
и
 называются равносильными
(при каждом испытании оба они либо
наступают, либо не наступают), если
называются равносильными
(при каждом испытании оба они либо
наступают, либо не наступают), если
 и
и
 то есть
то есть
 .
Например, если один раз подбросить
правильную игральную кость, то выпадение
нечётного числа будет событием
равносильным событию
.
.
Например, если один раз подбросить
правильную игральную кость, то выпадение
нечётного числа будет событием
равносильным событию
.
Cобытия
называются совместными,
если они могут наступить одновременно,
пересечение множеств элементарных
исходов, соответствующих этим событиям
не является пустым:
 .
Например, совместны события
.
Например, совместны события
 и
и
 ,
при извлечении наудачу из колоды карт
одной карты. События называются
несовместными,
если они не могут наступить одновременно,
а пересечение множеств элементарных
исходов, соответствующих этим событиям
является пустым:
,
при извлечении наудачу из колоды карт
одной карты. События называются
несовместными,
если они не могут наступить одновременно,
а пересечение множеств элементарных
исходов, соответствующих этим событиям
является пустым:
 (рис.2).
(рис.2).
Например,
несовместны события
|
|
Рисунок 2. Несовместные события и . |
Если рассматривать случайные события с точки зрения теории множеств, можно определить операции над ними. Суммой случайных событий называется случайное событие, состоящее в том, что хотя бы одно из суммируемых событий происходит. Множества элементарных исходов, соответствующие этим событиям объединяются (рис.3).
Свойства суммы событий:
|
|
Рисунок
3. Объединение множеств
и
: |
Пример.
Пусть из колоды карт наудачу извлекается
одна карта. Событие
 ,
событие
.
Тогда суммой событий
и
будет
событие
,
событие
.
Тогда суммой событий
и
будет
событие
 .
.
Произведением случайных событий называется случайное событие, состоящее в том, что одновременно наступают все перемножаемые события. Множества элементарных исходов, соответствующие этим событиям пересекаются (рис.4).
Свойства произведения событий:
|
|
Рисунок
4.
Пересечение множеств
и
: |
Пример.
Пусть из колоды карт наудачу извлекается
одна карта. Событие
,
событие
.
Тогда произведением событий
и
будет
событие
 .
.
Пример.
Пусть из колоды карт наудачу извлекается
одна карта. Если случайное событие
 ,
событие
,
событие
 ,
а событие
,
а событие
 ,
то событие
,
то событие
 .
.
Операции сложения и произведения случайных событий удовлетворяют свойству дистрибутивности:


Операции сложения и произведения случайных событий удовлетворяют формулам Моргана:


Разностью
случайных событий
и
называется случайное событие
 ,
состоящее в том, что событие
происходит, а событие
не
происходит. Множество элементарных
исходов, соответствующее событию
представляет
собой разность множеств элементарных
исходов, соответствующих событиям
и
(рис.5,
6).
,
состоящее в том, что событие
происходит, а событие
не
происходит. Множество элементарных
исходов, соответствующее событию
представляет
собой разность множеств элементарных
исходов, соответствующих событиям
и
(рис.5,
6).
|
|
Рисунок
5. Разность множеств
и
: |
Рисунок
6. Разность множеств
и
: |
Пример.
Пусть из колоды карт наудачу извлекается
одна карта. Событие
,
событие
.
Тогда разностью событий
![]() и
будет событие
и
будет событие
 .
А разностью событий
и
будет событие
.
А разностью событий
и
будет событие
 .
.
Событие
 (такое, что непоявление события
влечёт за собой появление события
(такое, что непоявление события
влечёт за собой появление события
 )
называется противоположным
событию
или его дополнением до
(рис.7).
)
называется противоположным
событию
или его дополнением до
(рис.7).
Свойства противоположных событий:
|
|
Рисунок 7. Событие противоположно событию . |
Задача.
Пусть
 - события, означающие попадание точки
соответственно в области
.
Что означает событие
- события, означающие попадание точки
соответственно в области
.
Что означает событие
 ?
?
Решение:
На диаграмме Эйлера-Венна событию
(рис.8) соответствует заштрихованная
область (пересечение множеств,
соответствующих событиям
 объединяется с множеством, соответствующим
событию
объединяется с множеством, соответствующим
событию
 ).
Чтобы произошло случайное событие
необходимо, чтобы одновременно произошли
события
или событие
.
).
Чтобы произошло случайное событие
необходимо, чтобы одновременно произошли
события
или событие
.
|
|
Рисунок 8. Диаграмма Эйлера-Венна, изображающая событие |
Рисунок 9. Диаграмма Эйлера-Венна. |
Какому случайному событию соответствует область, заштрихованная на рисунке 9.
Пример
«Возраст супругов». В демографии
изучается распределение по возрасту
супружеских пар. Пусть
 -
возраст мужа;
-
возраст мужа;
 -
возраст жены. Каждое наблюдение даёт
пару чисел
-
возраст жены. Каждое наблюдение даёт
пару чисел
 ;
- I
квадрант декартовой плоскости
;
- I
квадрант декартовой плоскости
 ;
каждая точка
- элементарный исход.
;
каждая точка
- элементарный исход.
Рассмотрим
случайные события:
|
|
Рис.10.
События
|
На рисунках представлены области, соответствующие случайным события:
 (рис.11.)
(рис.11.)
 (рис.12.)
(рис.12.)
 (рис.13).
(рис.13).
 (рис.14.)
(рис.14.)
 (рис.15.)
(рис.15.)
|
|
|
Рисунок
11. Событие
|
Рисунок
13. Событие |
Рисунок
15. Событие
|
|
|
|
Рисунок
12. Событие
|
Рисунок
14. Событие
|
События
 образуют
полную
группу попарно несовместных событий,
если любые два из них несовместны, и
хотя бы одно из них непременно должно
произойти в результате испытания:
образуют
полную
группу попарно несовместных событий,
если любые два из них несовместны, и
хотя бы одно из них непременно должно
произойти в результате испытания:
1.
 - свойство полноты
- свойство полноты
2.
 ,
,
 - свойство попарной несовместности.
- свойство попарной несовместности.
Пример.
Пусть один раз подбрасывают правильную
игральную кость. Случайные события
 ,
,
![]() образуют
полную группу событий. Случайные события
образуют
полную группу событий. Случайные события
 и
и
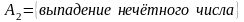 противоположны и также образуют полную
группу событий.
противоположны и также образуют полную
группу событий.
Классическое
определение вероятности может
быть сформулировано если элементарные
исходы образующие
несовместны, равновозможны и образуют
полную группу. Тогда вероятностью
события А
называется отношение количества
элементарных исходов из множества
,
благоприятствующих этому событию
(исход
 из множества
,
который приводит к наступлению события
(т.е.
из множества
,
который приводит к наступлению события
(т.е.
 ),
называется благоприятствующим событию
),
к общему числу всех исходов испытания,
составляющих
:
),
называется благоприятствующим событию
),
к общему числу всех исходов испытания,
составляющих
:
 .
.
Для вычисления числа благоприятствующих рассматриваемому событию исходов и общего числа исходов широко используются формулы комбинаторики.
Легко заметить, что вероятность любого события удовлетворяет свойствам:
1.
Вероятность случайного события есть
положительное число, заключенное между
нулем и единицей

2. Вероятность невозможного события равна нулю:
![]()
3. Вероятность достоверного события равна единице:
![]()
4.
Вероятность суммы несовместных событий
равна сумме вероятностей этих событий
(т.е. если
 ):
):
![]() .
.
Комбинаторикой называется раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству.
Правило
суммы.
Если некоторый объект
можно выбрать
 способами, а объект
-
способами, а объект
-
 способами (не такими, как
),
то объект «либо
,
либо
»
можно выбрать
способами (не такими, как
),
то объект «либо
,
либо
»
можно выбрать
 способами:
способами:
 .
.
Правило
произведений.
Если некоторый объект
можно выбрать
способами, а после каждого такого выбора
другой объект
можно выбрать (независимо от выбора
объекта
)
способами, то пары объектов «
и
»
можно выбрать
 способами:
способами:
 .
.
Генеральной
совокупностью без повторений
называется набор некоторого конечного
числа различных элементов:
 .
Генеральная
совокупность с повторениями
– это набор элементов
.
Генеральная
совокупность с повторениями
– это набор элементов
 различных классов, когда все элементы,
принадлежащие одному классу, считаются
одинаковыми:
различных классов, когда все элементы,
принадлежащие одному классу, считаются
одинаковыми:
 ,
где
,
где
 -
элементы 1-го класса,
-
элементы 1-го класса,
 -
элементы 2-го класса, …
-
элементы 2-го класса, …
 -
элементы
-го
класса. Выборкой объёма
-
элементы
-го
класса. Выборкой объёма
 называется произвольная группа из
элементов
данной генеральной совокупности.
называется произвольная группа из
элементов
данной генеральной совокупности.
Размещения – это комбинации, формируемые из различимых элементов по элементов в каждой и отличающиеся одна от другой либо составом, либо порядком следования элементов, размещенных в виде последовательностей.
Перестановки – это последовательности, каждая из которых состоит из различимых элементов и отличается одна от другой только порядком следования элементов, т.е. это размещения из n элементов по .
Сочетания – это комбинации, формируемые из различимых элементов по в каждой и отличающиеся одна от другой только составом элементов.
Формулы для подсчёта размещений, перестановок и сочетаний элементов приведены в таблице 1.
Таблица 1.
Вид выборки |
Выборка без повторений |
Выборка с повторениями (из элементов различных классов) |
Число размещений |
|
|
Число перестановок |
|
|
Число сочетаний |
|
|
-
количество элементов в выборке
(перестановке), причём
 элементов выборки извлечены из
элементов выборки извлечены из
 -го
класса
-го
класса
 .
.
Важная
задача, которую можно решить с
использованием формулы классической
вероятности – задача о распределении
частиц по ячейкам.
Пусть имеются
частиц, каждая из которых может находиться
с одной и той же вероятностью
 в каждой из
в каждой из
 ячеек. Найти вероятность того, что:
ячеек. Найти вероятность того, что:
- в определённых ячейках окажется по 1 частице;
- в каких-то ячейках окажется по 1 частице.
В
статистике
Больцмана
равновесными считаются любые мыслимые
распределения, отличающиеся не только
числом, но и индивидуальностью частиц:
в каждой ячейке может помещаться любое
число частиц от 0 до
.
Общее число возможных распределений
частиц
по
 ячейкам:
ячейкам:
 (каждая частица может находиться в
каждой из
ячеек,
частиц
распределяется по ячейкам),
(каждая частица может находиться в
каждой из
ячеек,
частиц
распределяется по ячейкам),
Вероятность
того, что в определённые
ячеек попадёт по одной частице:
 .
Во втором случае (
произвольных ячеек) число благоприятствующих
случаев будет в
.
Во втором случае (
произвольных ячеек) число благоприятствующих
случаев будет в
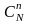 раз больше, и вероятность того, что в
какие-то
ячеек попадёт по одной частице равна:
раз больше, и вероятность того, что в
какие-то
ячеек попадёт по одной частице равна:
 .
.
В
статистике
Бозе-Эйнштейна
тождественными считаются случаи, когда
частицы меняются местами между ячейками
(причём важно число частиц в ячейке, а
не их индивидуальность) и полная группа
равновероятных событий состоит из
всевозможных распределений
частиц
по
ячейкам, причём за одно распределение
принимается целый класс больцмановских
распределений, отличающихся не числами
содержащихся в определённых ячейках
частиц, а только самими частицами.
Рассмотрим, например, случай
 .
Возможные расположения 2 частиц по 4
ячейкам представлены в таблице 2:
.
Возможные расположения 2 частиц по 4
ячейкам представлены в таблице 2:
Таблица 2.
случаи |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
ячейки |
ab |
|
|
|
a |
a |
a |
|
|
b |
b |
b |
|
|
|
|
|
ab |
|
|
b |
|
|
a |
a |
a |
|
|
b |
b |
|
|
|
|
|
ab |
|
|
b |
|
b |
|
|
a |
|
a |
|
a |
b |
|
|
|
|
ab |
|
|
b |
|
b |
|
|
a |
|
a |
b |
a |
a, b - наименования частиц
В статистике Бозе-Эйнштейна 5 и 10, 6 и 11, 7 и 12, 8 и 13, 9 и 14, 15 и 16 – попарно отождествляются (то есть имеется 10 равновозможных событий). А в статистике Больцмана, все 16 возможностей являются различными равновероятными событиями.
Число
всевозможных размещений частиц по
ячейкам можно получить предполагая,
что ячейки расположены на прямой вплотную
друг к другу. Необходимо рассмотреть
всевозможные перестановки частиц и
перегородок между ячейками (так будут
учтены всевозможные случаи заполнения
ячеек, отличающиеся как порядком
расположения частиц в ячейках, так и
порядком расположения перегородок).
Число этих перестановок
 Среди перестановок имеются и тождественные:
каждое распределение по ячейкам считается
Среди перестановок имеются и тождественные:
каждое распределение по ячейкам считается
 раз (так как различается, какие перегородки
были между ячейками), каждое распределение
по ячейкам также учитывается по
раз (так как различается, какие перегородки
были между ячейками), каждое распределение
по ячейкам также учитывается по
 раз (поскольку учитывалось не только
число частиц в ячейке, но и порядок их
расположения). Таким образом, каждое
распределение по ячейкам считается
раз (поскольку учитывалось не только
число частиц в ячейке, но и порядок их
расположения). Таким образом, каждое
распределение по ячейкам считается
 раз, поэтому число различных в смысле
Бозе-Эйнштейна распределений частиц
по ячейкам равно
раз, поэтому число различных в смысле
Бозе-Эйнштейна распределений частиц
по ячейкам равно
 .
Поэтому число равновероятных событий
в полной группе событий равно:
.
Поэтому число равновероятных событий
в полной группе событий равно:


В
статистике
Ферми-Дирака
в ячейке может находиться либо одна
частица, либо ни одной. Индивидуальность
частиц уничтожается. Общее число
распределений частиц по ячейкам
рассчитывается по схеме: первая частица
может быть расположена
различными
способами, вторая -
 ,
третья -
,
третья -
 ,
и т.д.,
-я
-
,
и т.д.,
-я
-
 способами. За различные способы
принимаются способы распределений,
отличающиеся перестановкой частиц по
ячейкам. Чтобы исключить индивидуальность
частиц, полученное число делится на
То есть
частиц
по
ячейкам могут быть распределены
способами. За различные способы
принимаются способы распределений,
отличающиеся перестановкой частиц по
ячейкам. Чтобы исключить индивидуальность
частиц, полученное число делится на
То есть
частиц
по
ячейкам могут быть распределены
 различными равновероятными способами.
Таким образом, искомые вероятности
будут равны:
различными равновероятными способами.
Таким образом, искомые вероятности
будут равны:


 Пример
показывает, как важно точно определить,
какие события считаются в задаче
равновероятными.
Пример
показывает, как важно точно определить,
какие события считаются в задаче
равновероятными.
Парадокс раздела ставки. Два игрока играют в безобидную игру (то есть у обоих шансы победить одинаковы), и они договорились, что тот, кто первым выиграет шесть партий, получит весь приз. Предположим, что игра остановилась до того, как один из них выиграл приз (например, первый выиграл 5 партий, а второй – 3). Как справедливо разделить приз?
Решение. Пачоли предлагал делить приз в отношении 5:3, Тарталья, в отношении 2:1. Но справедливым является раздел 7:1, предложенный Ферма и Паскалем. Они рассмотрели задачу как задачу о вероятностях. Справедливым предполагался такой раздел, который пропорционален шансам первого игрока выиграть приз. Ферма предложил продолжить игру тремя фиктивными партиями, даже если некоторые из них окажутся лишними (то есть когда один из игроков уже выиграл приз). Результаты партий представлены в таблице (Табл. 3.). Такое предположение делает все 8 возможных исходов игры равновероятными. Поскольку второй игрок получает приз только при одном исходе из восьми (результат этой игры расположен в последнем столбце – второй игрок выигрывает все три партии), а в остальных случаях побеждает первый игрок, справедлив раздел 7:1.
Таблица 3.
Номер игры |
Распределение выигрышей |
|||||||
1 игра |
10 |
10 |
10 |
01 |
10 |
01 |
01 |
01 |
2 игра |
10 |
10 |
01 |
10 |
01 |
10 |
01 |
01 |
3 игра |
10 |
01 |
10 |
10 |
01 |
01 |
10 |
01 |
 1-
выигрыш, 0 – проигрыш игрока; первый
столбец – результата игры первого
игрока, второй - второго
1-
выигрыш, 0 – проигрыш игрока; первый
столбец – результата игры первого
игрока, второй - второго
Пример. Из генеральной совокупности объёма извлекается с возвращением выборка объёма . Рассмотрим событие, состоящее в том, что все элементы выборки различны (то есть выборка может быть получена при выборе без возвращения).
Решение.
Различных выборок с возвращением
существует
 ,
из них
,
из них
 обладают указанным свойством. Приписывая
всем точкам пространства элементарных
исходов равные вероятности, получим,
что вероятность отсутствия одинаковых
элементов в выборке равна:
обладают указанным свойством. Приписывая
всем точкам пространства элементарных
исходов равные вероятности, получим,
что вероятность отсутствия одинаковых
элементов в выборке равна:

если шаров разместить по ячейкам, то вероятность того, что каждая ячейка будет занят
 .
Например, при
.
Например, при

 ,
то есть если в городе каждую неделю
происходит 7 автомобильных катастроф,
то (в предположении, что все возможные
распределения равновероятны) практически
каждая неделя будет содержать дни,
когда происходит две или более катастрофы.
Равномерное распределение числа
катастроф встречается, в среднем, для
одной недели из 165.
,
то есть если в городе каждую неделю
происходит 7 автомобильных катастроф,
то (в предположении, что все возможные
распределения равновероятны) практически
каждая неделя будет содержать дни,
когда происходит две или более катастрофы.
Равномерное распределение числа
катастроф встречается, в среднем, для
одной недели из 165.дни рождения людей образуют выборку объёма из генеральной совокупности всех дней в году (годы имеют разную длину, и рождаемость в разные месяцы не постоянна, но в первом приближении можно считать, что случайный выбор людей приводит к случайному выбору дней рождения). Итак,
 ,
тогда вероятность того, что все
,
тогда вероятность того, что все
 дней рождения различны, равна
дней рождения различны, равна

Например,
для
 ,
,
 (то есть с вероятностью более 50% среди
23 человек найдутся, по крайне мере двое,
имеющие общий день рождения).
(то есть с вероятностью более 50% среди
23 человек найдутся, по крайне мере двое,
имеющие общий день рождения).
Несложно
получить простую числовую оценку
 .
Если
мало, то можно пренебречь произведениями,
содержащими более, чем по одному
сомножителю и написать грубое приближение:
.
Если
мало, то можно пренебречь произведениями,
содержащими более, чем по одному
сомножителю и написать грубое приближение:
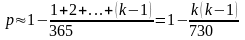 (при
(при
 точное значение
точное значение
 ;
приближённое
).
При больших
;
приближённое
).
При больших
 ,
тогда
,
тогда
 .
При
.
При
 абсолютная
ошибка формулы составляет менее, чем
0,08.
абсолютная
ошибка формулы составляет менее, чем
0,08.
Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречается испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. По этой причине наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение.
Если
распределение всех возможных исходов
испытания непрерывно и бесконечно,
можно использовать понятие геометрической
вероятности – то есть вероятности
попадания точки в область. При определении
геометрической вероятности полагают,
что имеется область
 и в ней меньшая область
и в ней меньшая область
 с квадрируемой границей. На
наудачу бросается точка. Случайное
событие
с квадрируемой границей. На
наудачу бросается точка. Случайное
событие
 .
Вероятность попадания в какую-либо
часть
пропорциональна мере этой части и не
зависит от её расположения и формы.
.
Вероятность попадания в какую-либо
часть
пропорциональна мере этой части и не
зависит от её расположения и формы.
Геометрической
вероятностью
события A
называется отношение меры области
,
благоприятствующей событию A
к мере всей области
:
 .
.
Область, на которую распространяется геометрическая вероятность может быть одномерной (у кривой или отрезка мерой является длина), двумерной (мера геометрической фигуры на плоскости – её площадь), трёхмерной (мера тела в пространстве – объём) или -мерной в общем случае.
Парадокс Бертрана. Для некоторой окружности случайным образом выбирается хорда. Найти вероятность того, что эта хорда длиннее стороны правильного треугольника, вписанного в данную окружность. Парадокс утверждает, что эта вероятность определяется неоднозначно (т.е. различные методы приводят к различным результатам).
Согласно
первому методу (рис.16) случайным образом,
равномерно, в данном круге выбирается
точка. Эта случайная точка определяет
единственную хорду, серединой которой
она является. Эта хорда длиннее стороны
правильного треугольника тогда и только
тогда, когда её середина лежит внутри
круга, вписанного в треугольник. Радиус
этого круга равен половине радиуса
исходного круга, следовательно, площадь
вписанного круга составляет
 площади исходного. То есть вероятность
того, что случайно выбранная точка лежит
внутри вписанного круга, равна
.
площади исходного. То есть вероятность
того, что случайно выбранная точка лежит
внутри вписанного круга, равна
.
По
второму методу (рис.17), исходя из
соображений симметрии, можно считать,
что одним концом хорды является
произвольная фиксированная точка на
окружности. Пусть этой точкой является
вершина вписанного треугольника. Выберем
другой конец случайно с равномерным
распределением. Вершины треугольника
делят окружность на три равные дуги, и
случайная хорда длиннее стороны
правильного треугольника, если она
пересекает этот треугольник. Теперь
искомая вероятность равна
 .
.
В
соответствии с третьим методом (рис.18),
выбирают точку случайным образом
равномерно на радиусе окружности и
берут хорду, которая перпендикулярна
этому радиусу и проходит через выбранную
точку. Тогда случайная хорда длиннее
стороны вписанного правильного
треугольника, если случайная точка
лежит на той половине радиуса, которая
ближе к центру. Исходя из соображений
симметрии, неважно какой радиус был
выбран для построения, поэтому искомая
вероятность равна
 .
.
Результат выглядит парадоксально, так как предполагается, что слова «равномерный случайный выбор» однозначно определяют искомую вероятность. Парадокс показывает, что возможны различные способы выбора равномерным образом, причём каждый способ выглядит «естественным». Каждый из трёх методов использует равномерное распределение (на круге, на окружности и на радиусе круга).
|
|
|
Рисунок 16. Взаимное расположение хорды и треугольника. Случай 1. |
Рисунок 17. Взаимное расположение хорды и треугольника. Случай 2. |
Рисунок 18. Взаимное расположение хорды и треугольника. Случай 3. |
Парадокс
заключён в том, что за решение одной и
той же задачи выдаются решения трёх
разных задач, поскольку не определено
понятие «проведение хорды наудачу». В
первом случае бросают одну точку наудачу
внутрь круга и ищут вероятность попадания
этой точки внутрь меньшего концентрического
круга (рис.19). Во втором решении стержень,
закреплённый на шарнире, расположенном
в одной из точек окружности заставляют
совершать колебания размером не более
 .
При этом предполагается, что остановка
стержня внутри дуги окружности длины
.
При этом предполагается, что остановка
стержня внутри дуги окружности длины
 зависит
только от длины дуги, но не от её положения.
То есть равновероятными событиями
считаются остановки стержня в любых
дугах окружности одинаковой длины
(рис.20). В третьем решении вдоль одного
из диаметров заставляют катиться круглый
цилиндрический стержень. Равновероятными
считаются события, состоящие в том, что
остановка произойдёт в интервале длины
,
где бы внутри диаметра не был расположен
этот отрезок (рис.21).
зависит
только от длины дуги, но не от её положения.
То есть равновероятными событиями
считаются остановки стержня в любых
дугах окружности одинаковой длины
(рис.20). В третьем решении вдоль одного
из диаметров заставляют катиться круглый
цилиндрический стержень. Равновероятными
считаются события, состоящие в том, что
остановка произойдёт в интервале длины
,
где бы внутри диаметра не был расположен
этот отрезок (рис.21).
Несогласованность
определений вероятности во втором и
третьем случаях становится очевидной
после расчёта. Вероятность того, что
стержень остановится в промежутке от
А до
(в третьем решении) равна
 .
Вероятность того, что проекция точки
пересечения стержня с окружностью во
втором решении попадёт в тот же интервал
(из геометрических соображений) равна:
.
Вероятность того, что проекция точки
пересечения стержня с окружностью во
втором решении попадёт в тот же интервал
(из геометрических соображений) равна:
 .
.
|
|
|
Рисунок 19. Множества и . Случай 1. |
Рисунок 20. Множества и . Случай 2. |
Рисунок 21. Множества и . Случай 3. |
Итак, причина неоднозначности решения лежит не в принципиальной невозможности определить вероятность для случаев бесконечного числа всевозможных исходов. Очевидно различие постановки задачи в трёх случаях.
Статистическая
вероятность определяется из опыта.
Пусть в неизменных условиях проводится
большое число
независимых друг от друга одинаковых
испытаний, в каждом из которых некоторое
событие A
может появиться или не появиться, и
фиксируется число появлений событий
A,
обозначаемое через
.
По данным наблюдений рассчитывают
отношение
 ,
называемое частостью (относительной
частотой, выборочной долей) события A,
где
,
называемое частостью (относительной
частотой, выборочной долей) события A,
где
 - частота события A.
- частота события A.
Статистической
вероятностью
события A
называется частость (относительная
частота) появления этого события в
произведённых
испытаниях:
 .
.
Наблюдаемая частость события A почти для любой большой серии указанных испытаний мало отклоняется от некоторой постоянной величины, то есть проявляется закон устойчивости частостей. Поэтому на практике за вероятность случайного события A принимают наблюдаемую частость (или число, близкое к этому значению).
Аксиоматическое определение вероятности случайного события создано в 1933 г. академиком Андреем Николаевичем Колмогоровым. Аксиомы теории вероятностей вводятся таким образом, чтобы вероятность события обладала основными свойствами статистической вероятности, характеризующей ее практический смысл.
Пусть
– множество всех возможных исходов
некоторого опыта (эксперимента),
 – алгебра событий. Совокупность
подмножеств множества
называется алгеброй (
– алгебра событий. Совокупность
подмножеств множества
называется алгеброй ( -алгеброй),
если выполнены следующие условия:
-алгеброй),
если выполнены следующие условия:
а) содержит невозможное и достоверное событие;
б)
если события
 ,
,
 ,
,
 ,
… (конечное или счетное множество)
принадлежат
,
то
принадлежит сумма, произведение и
дополнение (то есть противоположное
для
,
… (конечное или счетное множество)
принадлежат
,
то
принадлежит сумма, произведение и
дополнение (то есть противоположное
для
 )
этих событий.
)
этих событий.
Вероятностью
называется функция
 ,
определенная на алгебре событий
,
принимающая действительные значения
и удовлетворяющая следующим аксиомам:
,
определенная на алгебре событий
,
принимающая действительные значения
и удовлетворяющая следующим аксиомам:
Аксиома
неотрицательности:
вероятность любого события
 неотрицательна, то есть
неотрицательна, то есть
 .
.
Аксиома нормированности: вероятность достоверного события равна единице, то есть
![]() .
.
Аксиома
аддитивности:
вероятность суммы несовместных событий
равна сумме вероятностей этих событий,
то есть если

 ,
то
,
то

Из аксиом теории вероятностей выводятся очевидные свойства вероятности.
1.
Вероятность невозможного события равна
нулю:
 .
.
Поскольку
 и
,
то согласно аксиоме аддитивности имеем
и
,
то согласно аксиоме аддитивности имеем
 ,
следовательно
.
,
следовательно
.
2.
Сумма вероятностей противоположных
событий равна единице:
 .
.
Поскольку
 ,
то
,
то
 ,
а так как
,
то в силу аксиом нормированности и
аддитивности получаем
или
,
а так как
,
то в силу аксиом нормированности и
аддитивности получаем
или
 .
.
3.
Вероятность любого события не превосходит
единицы:
 .
.
Из
свойства
вытекает, что
 ,
с учетом аксиомы неотрицательности
получаем
.
,
с учетом аксиомы неотрицательности
получаем
.
4.
Если
,
то есть событие
влечет за собой событие
,
то:
 .
.
Так
как
 при
и
при
и
![]() ,
то согласно аксиоме аддитивности
получаем
,
то согласно аксиоме аддитивности
получаем
 .
Но
.
Но
 (аксиома неотрицательности):
(аксиома неотрицательности):
5.
Если события
,
,
,
…,
 образуют полную
группу несовместных событий,
то есть:
образуют полную
группу несовместных событий,
то есть:
 и
,
то
и
,
то
 .
.
6.
Если события совместны, то вероятность
их суммы равна сумме их вероятностей
без вероятности их произведения:

Представим
события
и
в виде суммы двух несовместных событий:
|
|
Рисунок 22. Диаграмма Эйлера-Венна, изображающая совместные события и |
Тогда,
согласно аксиоме аддитивности,
 и
и
 .
Отсюда следует
.
.
Отсюда следует
.
Можно получить формулу вероятности суммы трех и большего числа совместных событий:



Задача.
Электрическая цепь составлена по схеме,
приведённой на рисунке. Выход из строя
элемента
 ,
где
,
где
 - это событие
,
элемента
– событие
и элемента
- это событие
,
элемента
– событие
и элемента
 ,
где
,
где
 - событие
- событие
 .
Записать события
.
Записать события
 и
и
 через
,
и
,
если случайное событие
- это разрыв цепи. Известно, что вероятность
отказа элемента
,
где
равна
через
,
и
,
если случайное событие
- это разрыв цепи. Известно, что вероятность
отказа элемента
,
где
равна
 ;
а вероятность отказа элемента
,
где
равна
;
а вероятность отказа элемента
,
где
равна
 .
Какова вероятность безотказной работы
цепи, схема которой представлена на
рисунке 23?
.
Какова вероятность безотказной работы
цепи, схема которой представлена на
рисунке 23?
Решение:
Рассчитаем вероятности безотказной
работы элементов
и
:
 ;
;
 .
По формулам умножения вероятностей и
сложения вероятностей совместных
событий вычислим вероятность случайного
события
.
По формулам умножения вероятностей и
сложения вероятностей совместных
событий вычислим вероятность случайного
события
 :
:

|
|
Рисунок 23. Схема электрической цепи. |
Рисунок 25. Схема электрической цепи. |
|
|
Рисунок 24. Схема электрической цепи. |
Рисунок 26. Схема электрической цепи. |
Решить аналогичные задачи для цепей, представленных на рис.24-26.
События и называются зависимыми, если появление одного из них изменяет вероятность появления другого. Несовместные события зависимы, так как появление любого из них обращает в нуль вероятности появления всех остальных.
Например,
если из урны, содержащей
чёрных и
белых шаров последовательно, без
возвращения извлекаются два шара, то
случайные события
 и
и
 зависимые, поскольку вероятность события
зависит от того, произошло или не
произошло событие
,
изменяющее количество и состав шаров
в урне.
зависимые, поскольку вероятность события
зависит от того, произошло или не
произошло событие
,
изменяющее количество и состав шаров
в урне.
Пусть и зависимые события. Условной вероятностью события при условии , называется вероятность события , вычисленная в предположении, что событие произошло. Эту вероятность можно найти по формуле
 .
.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго

В противном случае, когда появление одного из случайных событий или не изменяет вероятности появления другого, события или называются независимыми. Если событие не зависит от события , то событие не зависит от события - свойство независимости событий взаимно.
Например,
при подбрасывании двух правильных монет
случайное событие
 и случайное событие
и случайное событие
 являются независимыми. Если несколько
раз подбрасывать одну и ту же правильную
монету, то появление герба не зависит
от того, появлялся ли герб в предыдущий
раз (монета «не помнит» результатов
предшествующего испытания). Соответствующие
события также независимы.
являются независимыми. Если несколько
раз подбрасывать одну и ту же правильную
монету, то появление герба не зависит
от того, появлялся ли герб в предыдущий
раз (монета «не помнит» результатов
предшествующего испытания). Соответствующие
события также независимы.
Если
два события
и
независимы,
то условная вероятность события
равна его безусловной вероятности:
 .
Вероятность совместного появления двух
независимых событий равна произведению
вероятностей этих событий. То есть, если
.
Вероятность совместного появления двух
независимых событий равна произведению
вероятностей этих событий. То есть, если
 и
и
 ,
то
,
то
 .
.
Верно также и обратное утверждение. На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.
Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события , , попарно независимы, если независимы события и , и , и . Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.
Основное свойство любого случайного события, независимо от его природы – вероятность его осуществления. Под вероятностью реального события понимается численная мера объективной возможности его появления.
Парадокс
Бернштейна. На плоскость бросают тетраэдр
три грани которого покрашены соответственно
в красный, синий и зелёный цвета, а на
четвёртую грань нанесены все три цвета.
Событие
 означает, что при бросании тетраэдра
на плоскость выпала грань, содержащая
красный цвет,
- грань, содержащая синий цвет
- грань, содержащая зелёный цвет. Поскольку
каждый из цветов содержится на двух
гранях, то
означает, что при бросании тетраэдра
на плоскость выпала грань, содержащая
красный цвет,
- грань, содержащая синий цвет
- грань, содержащая зелёный цвет. Поскольку
каждый из цветов содержится на двух
гранях, то
 .
Вероятности
.
Вероятности
 ,
так как пара цветов присутствует только
на одной грани. Это означает попарную
независимость всех трёх событий. Но
,
так как пара цветов присутствует только
на одной грани. Это означает попарную
независимость всех трёх событий. Но
 .
События
,
,
не являются независимыми в совокупности.
.
События
,
,
не являются независимыми в совокупности.
Парадокс независимости. Предположим, что бросают две правильные монеты. Пусть событие А – «на первой монете выпал герб», событие В – «на второй монете выпал герб», и событие С – «на одной (и только на одной монете) выпал герб». Тогда А, В и С попарно независимы, но любые два из них однозначно определяют третье.
А
и В независимы, поскольку результаты
первого бросания не зависят от результатов
второго. С другой стороны, события А и
С (а так же В и С) на первый взгляд кажутся
зависимыми, на так как
и, аналогично,
 ,
они, на самом деле, независимы. Справедливо
также, что любые два события определяют
третье, поскольку каждое событие (А, В
и С) происходит тогда и только тогда,
происходит ровно одно из двух других
событий. Этот феномен показывает, что
попарная независимость событий не
означает их независимость в совокупности.
,
они, на самом деле, независимы. Справедливо
также, что любые два события определяют
третье, поскольку каждое событие (А, В
и С) происходит тогда и только тогда,
происходит ровно одно из двух других
событий. Этот феномен показывает, что
попарная независимость событий не
означает их независимость в совокупности.
События
из некоторой совокупности взаимно
независимы если для любого конечного
набора событий из этой совокупности
 выполняется свойство мультипликативности:
выполняется свойство мультипликативности:
 то есть вероятность совместного события
равна произведению индивидуальных
(маргинальных) вероятностей.
то есть вероятность совместного события
равна произведению индивидуальных
(маргинальных) вероятностей.
Парадокс условной вероятности. Существуют события А, В и С такие, что:
- условная вероятность события А, при условии, что событие В произошло меньше, чем условная вероятность события А, при условии, что В не произошло;
- условная вероятность события А, при условии, что произошли оба события В и С, больше условной вероятности А при условии, что С наступило, а В нет;
- условная вероятность события А относительно В и дополнение к С больше условной вероятности А при условии, что ни В ни С не произошли.
Формально
эти условия можно записать:
 ;
;
 ;
;
 .
Результат представляется парадоксальным
так как можно подумать, что
.
Результат представляется парадоксальным
так как можно подумать, что
 - среднее величин
- среднее величин
 и
и
 ,
аналогично
- среднее величин
,
аналогично
- среднее величин
 и
и
 ,
а среднее двух средних величин должно
быть меньше среднего двух больших
величин. Объяснение этого ошибочного
заключения состоит в том, что
и
являются
взвешенными средними указанных выше
вероятностей, причём соответствующие
веса в обоих случаях различны:
,
а среднее двух средних величин должно
быть меньше среднего двух больших
величин. Объяснение этого ошибочного
заключения состоит в том, что
и
являются
взвешенными средними указанных выше
вероятностей, причём соответствующие
веса в обоих случаях различны:
 в
то время как
в
то время как

Тем
не менее, если события В и С независимы,
то
 и
и
 ,
так что в этом случае парадокса не
возникает.
,
так что в этом случае парадокса не
возникает.
|
Если
событие
может наступить лишь с одним из событий
(гипотез)
|
Рисунок 27. Полная группа событий и событие . |
Если
стал известен результат испытания, в
итоге которого появилось событие А
(событие
произошло), то вероятности гипотез
 можно переоценить, т.е. найти условные
вероятности
можно переоценить, т.е. найти условные
вероятности
 по формулам
Байеса:
по формулам
Байеса:

Исходные вероятности называются априорными, а вероятности апостериорными.
При
практическом применении теории
вероятностей часто приходится встречаться
с задачами, в которых один и тот же опыт
или аналогичные опыты повторяются
неоднократно. Повторные
независимые испытания
– это многократные испытания, в которых
вероятность появления события A
в каждом испытании не меняется в
зависимости от исходов других испытаний
(вероятность наступления события
в каждом из независимых испытаний
постоянна и равна
;
вероятность противоположного события,
состоящего в том, что событие
не происходит в одном испытании, обычно
обозначается как
 ).
В подобных задачах, исследователя
интересует не результат каждого
отдельного опыта, а общее число появлений
события
в
опытах из
.
).
В подобных задачах, исследователя
интересует не результат каждого
отдельного опыта, а общее число появлений
события
в
опытах из
.
Например, если производится серия выстрелов по одной и той же цели, важен не результат каждого выстрела, а общее число попаданий. Повторными испытаниями можно назвать также одновременное проведение одинаковых опытов. Например, при контроле уровня надежности прибора можно либо проводить испытаний с одним и тем же прибором (если после отказа полностью восстанавливают его исходные свойства), либо ставить на испытания опытных образцов этого прибора, которые считают идентичными.
Схему
повторных независимых испытаний для
частного случая
 (где
-
количество исходов отдельного испытания)
рассмотрел Якоб Бернулли (1654 – 1705).
Формула
Бернулли
позволяет
вычислить вероятность того, что в n
независимых испытаниях, в каждом из
которых вероятность появления события
равна
(
(где
-
количество исходов отдельного испытания)
рассмотрел Якоб Бернулли (1654 – 1705).
Формула
Бернулли
позволяет
вычислить вероятность того, что в n
независимых испытаниях, в каждом из
которых вероятность появления события
равна
( ),
событие наступит ровно
раз (безразлично в какой последовательности)
равна:
),
событие наступит ровно
раз (безразлично в какой последовательности)
равна:
 ,
где
.
,
где
.
Формула
Бернулли применяется при небольших
значениях
 .
.
Число
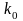 наступлений события A
в повторных независимых испытаниях, в
каждом их которых вероятность наступления
события A
равна
,
называют наивероятнейшим
числом наступлений события,
если вероятность того, что событие
наступит в этих испытаниях
раз, превышает (или, по крайней мере, не
меньше) вероятности остальных, возможных
исходов испытаний. Наивероятнейшее
число определяется из двойного
неравенства:
наступлений события A
в повторных независимых испытаниях, в
каждом их которых вероятность наступления
события A
равна
,
называют наивероятнейшим
числом наступлений события,
если вероятность того, что событие
наступит в этих испытаниях
раз, превышает (или, по крайней мере, не
меньше) вероятности остальных, возможных
исходов испытаний. Наивероятнейшее
число определяется из двойного
неравенства:
 ,
где
.
,
где
.
Принято считать, что:
1)
если
 дробное число, то существует одно
наивероятнейшее число
;
дробное число, то существует одно
наивероятнейшее число
;
2)
если
целое число, то существует два
наивероятнейших числа
 и
и
 ;
;
3)
если
 -
целое число, то наивероятнейшее число
-
целое число, то наивероятнейшее число
 .
.
Теорема
Пуассона.
Если вероятность
наступления события
в каждом из независимых испытаний
постоянна, но близка к нулю
 ,
а число повторных испытаний
достаточно велико
,
а число повторных испытаний
достаточно велико
 ,
то вероятность того, что в
независимых испытаниях событие наступит
ровно
раз (безразлично в какой последовательности),
приближенно равна
,
то вероятность того, что в
независимых испытаниях событие наступит
ровно
раз (безразлично в какой последовательности),
приближенно равна
 ,
где
,
где
 ,
,
 .
.
Пользоваться
формулой Бернулли при больших значениях
 достаточно трудно, так как формула
требует выполнения действий над огромными
числами. Локальная теорема Лапласа и
дает асимптотическую формулу, которая
позволяет приближенно найти вероятность
появления события в
испытаниях ровно
раз, если число испытаний достаточно
велико.
достаточно трудно, так как формула
требует выполнения действий над огромными
числами. Локальная теорема Лапласа и
дает асимптотическую формулу, которая
позволяет приближенно найти вероятность
появления события в
испытаниях ровно
раз, если число испытаний достаточно
велико.
Локальная теорема Лапласа. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна ( ), событие наступит ровно раз (безразлично в какой последовательности), приближенно равна
 ,
где
,
,
где
,
 ,
,
 .
.
Функция
 называется дифференциальной функцией
Лапласа, а ее график – кривой Гаусса.
Данный график представлен на рисунке
28.
называется дифференциальной функцией
Лапласа, а ее график – кривой Гаусса.
Данный график представлен на рисунке
28.
Свойства дифференциальной функции Лапласа:
1.
 - чётная функция, т.е.
- чётная функция, т.е.
 ;
;
2.
при

 .
.
Рисунок 28. График дифференциальной функции Лапласа
|
|
Интегральная
теорема Муавра-Лапласа.
Вероятность того, что в
независимых испытаниях, в каждом из
которых вероятность появления события
равна
(
),
событие наступит не менее
 раз и не более
раз и не более
 раз, приближенно равна
раз, приближенно равна
 ,
,
где
 ,
,
 .
.
Это равенство тем точнее, чем больше .
Функция называется интегральной функцией Лапласа. График функции представлен на рисунке 16.
Свойства интегральной функции Лапласа:
Функция
 нечетная, т.е.
нечетная, т.е.
 ;
;При
 можно считать, что
=0,5.
можно считать, что
=0,5.
Рисунок 29. График интегральной функции Лапласа
|
|
Точное определение случайной величины дать сложно, поэтому можно ограничиться её описанием. Случайной называют величину, которая в результате опыта может принять то или иное возможное значение, заранее неизвестное, но обязательно одно.
Если
множество возможных значений случайной
величины конечно или счётно, то случайная
величина дискретна. Например
 – количество очков, выпавшее при одном
бросании игральной кости (возможные
значения этой случайной величины: 1, 2,
3, 4, 5, 6), или
– количество очков, выпавшее при одном
бросании игральной кости (возможные
значения этой случайной величины: 1, 2,
3, 4, 5, 6), или
 – число
появлений герба при выбрасывании двух
правильных монет (ее возможные значения
0, 1, 2). Также дискретной случайной
величиной является
– число
появлений герба при выбрасывании двух
правильных монет (ее возможные значения
0, 1, 2). Также дискретной случайной
величиной является
 - количество студентов, присутствующих
на лекции.
- количество студентов, присутствующих
на лекции.
Если множество возможных значений
случайной величины – весь числовой
промежуток (конечный или бесконечный),
то случайную величину называют
непрерывной. Непрерывна случайная
величина
 – расстояние,
которое пролетит камень, брошенный под
углом к горизонту (её возможные значения
принадлежат некоторому промежутку
– расстояние,
которое пролетит камень, брошенный под
углом к горизонту (её возможные значения
принадлежат некоторому промежутку
 ),
или
),
или
 – время безотказной работы телевизора
(возможные значения принадлежат
промежутку
– время безотказной работы телевизора
(возможные значения принадлежат
промежутку
 ,
где Т
– максимальное время работы).
,
где Т
– максимальное время работы).
Закон
распределения дискретной случайной
величины
– это функция, сопоставляющая каждому
возможному значению
 случайной величины ее вероятность
случайной величины ее вероятность
 ,
,
 ,
причем
,
причем
 .
Закон распределения полностью
характеризует дискретную случайную
величину, указывая все возможные
значения, которые она принимает и
вероятности, с которыми эти значения
появляются в результате опыта.
.
Закон распределения полностью
характеризует дискретную случайную
величину, указывая все возможные
значения, которые она принимает и
вероятности, с которыми эти значения
появляются в результате опыта.
Если
дискретная случайная величина Х
принимает конечное множество значений
 ,
,
 ,….,
,….,
 с вероятностями
с вероятностями
 ,
,
 ,….,
,….,
 ,
то аналитически ее закон распределения
определяется формулами:
,
то аналитически ее закон распределения
определяется формулами:
 ,
,
,
,
 .
.
если
случайная величина Х
принимает счётное множество значений
,
,….,
,
… с вероятностями
,
,….,
,
…, то аналитически ее закон распределения
определяется аналогично
 .
.
Два множества называются равномощными, если между их элементами можно установить взаимно однозначное соответствие. Множество равномощное множеству всех натуральных чисел называется счётным.
Результаты вычислений вероятностей представляют в таблице (называемой иначе рядом распределения):
Таблица 4.
|
|
|
… |
|
|
|
|
… |
|
Графически
закон распределения может быть представлен
многоугольником
распределения
(или полигоном)
случайной величины Х.
Чтобы построить такой график в декартовой
системе координат строят точки
 и соединяют их отрезками прямых, чтобы
получилась ломаная линия (рис. 30)).
и соединяют их отрезками прямых, чтобы
получилась ломаная линия (рис. 30)).
Рисунок
30. Многоугольник распределения
(полигон) дискретной случайной величины
|
|
Непрерывные случайные величины делятся на два класса: абсолютно непрерывные случайные величины и смешанные (обладающие свойствами как дискретных, так и непрерывных случайных величин). Случайная величина называется абсолютно непрерывной, если ее функция распределения является непрерывно дифференцируемой. Смешанные случайные величины имеют кусочно-непрерывную функцию распределения со счетным (или конечным) множеством точек разрыва первого рода (скачков).
Функцией распределения (или интегральной функцией распределения) случайной величины Х называется функция
 ,
,

(вероятность того, что случайная величина Х в результате испытания примет значение, меньшее, чем х).
Свойства функции распределения.
 – по
определению.
– по
определению. ;
;

Событие,
заключающееся в том, что случайная
величина Х
примет значение меньшее
 ,
невозможно, а событие, заключающееся в
том, что случайная величина Х
примет значение
,
невозможно, а событие, заключающееся в
том, что случайная величина Х
примет значение
 ,
достоверно. Если
,
достоверно. Если
 ,
то
,
то
 при
при
 ,
,
 при
при
 .
.
 – монотонно
неубывающая функция. Это означает, что
– монотонно
неубывающая функция. Это означает, что
 при
при
 .
.
 .
.
является непрерывной слева (в случае смешанной или дискретной случайной величины), т.е.:
 (или
(или
 )
(рис.31).
)
(рис.31).
Рисунок. 31. График функции распределения дискретной случайной величины . |
|
 Вероятность
того, что непрерывная случайная величина
Х
примет одно определенное значение,
равна нулю. Поэтому:
Вероятность
того, что непрерывная случайная величина
Х
примет одно определенное значение,
равна нулю. Поэтому:
 .
.
Функцию распределения дискретной случайной можно определить следующим образом:
 .
.
Пусть Х – непрерывная случайная величина, тогда – ее функция распределения дифференцируема всюду, за исключением, быть может, конечного числа точек. На рисунке представлена функция, не являющаяся дифференцируемой в точках и (рис. 32).
Рисунок 32. График функции распределения непрерывной случайной величины , не являющейся дифференцируемой в точках и .
|
|
Производная
 функции распределения называется
плотностью
распределения вероятностей
функции распределения называется
плотностью
распределения вероятностей
 непрерывной случайной величины Х
или
иначе дифференциальной функцией
(дифференциальным законом)
распределения
непрерывной случайной величины Х.
непрерывной случайной величины Х
или
иначе дифференциальной функцией
(дифференциальным законом)
распределения
непрерывной случайной величины Х.
Поскольку по определению производной функции:
 ,
а
,
а
 (по свойству функции распределения), то
(по свойству функции распределения), то
 – вероятность, отнесенная к единице
длины или «средняя вероятность» и предел
этого отношения естественно называть
плотностью вероятности.
– вероятность, отнесенная к единице
длины или «средняя вероятность» и предел
этого отношения естественно называть
плотностью вероятности.
Поэтому
плотностью
распределения вероятностей случайной
величины Х в точке х
называется предел отношения вероятности
попадания значений этой величины в
интервал
 к длине интервала
к длине интервала
 ,
когда
,
когда
 :
:
 .
.
Свойства плотности распределения вероятностей.
 в
точках, где существует
;
в
точках, где существует
;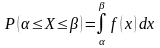 ;
; (условие
нормировки).
(условие
нормировки).
Функцию
распределения
по известной плотности вероятности
можно найти по формуле:
 .
.
Закон распределения полностью характеризует случайную величину, но чаще всего этот закон неизвестен, а в распоряжении исследователя имеются только частичные сведения. Но для решения большинства практических задач и не требуется полная информация о случайной величине, достаточно указать некоторые числовые параметры, позволяющие в компактной форме отразить её существенные особенности. Эти параметры называются числовыми характеристиками случайной величины. Среди них различают характеристики положения (математическое ожидание, мода, медиана и др.), характеристики рассеивания (дисперсия, среднеквадратичное отклонение) и характеристики формы распределения (различные моменты порядка выше первого, коэффициенты асимметрии и эксцесса).
Пусть
Х
– дискретная случайная величина с
законом распределения, представленным
таблицей 3. Математическим
ожиданием дискретной случайной величины
называется число
 .
.
Пусть
Х
– непрерывная случайная величина и
– ее
плотность вероятности.
Математическим
ожиданием
непрерывной
случайной величины Х
называется число
 (если этот интеграл сходится).
(если этот интеграл сходится).
Ели
значения случайной величины (дискретной
или непрерывной) занимают промежуток
,
то ее математическое ожидание всегда
находится между ее крайними значениями:
 .
Математическое ожидание изменяется в
тех же единицах, что и случайная величина
.
.
Математическое ожидание изменяется в
тех же единицах, что и случайная величина
.
Если
распределение случайной величины
обладает свойством симметрии, то есть
если график плотности вероятности (для
непрерывной случайной величины) или
многоугольник распределения (для
дискретной случайной величины) симметричен
относительно прямой
 ,
то математическое ожидание этой
случайной величины
,
то математическое ожидание этой
случайной величины
 .
(Рис. 33).
.
(Рис. 33).
Рисунок 33. График функции плотности вероятности непрерывной случайной величины , симметричный относительно прямой . |
|



 и
при извлечении наудачу из колоды карт
одной карты.
и
при извлечении наудачу из колоды карт
одной карты.














 .
. .
.







 ,
,
 и
и
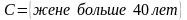 .
Событию
.
Событию
 соответствуют точки, лежащие справа
от прямой
соответствуют точки, лежащие справа
от прямой
 .
Событию
соответствует
область, расположенная между осью
.
Событию
соответствует
область, расположенная между осью
 и
прямой
и
прямой
 .
Событию
.
Событию
 соответствует часть I
квадранта декартовой плоскости,
расположенная над прямой
соответствует часть I
квадранта декартовой плоскости,
расположенная над прямой
 (рис.10).
(рис.10).




 .
. .
.


 .
. .
. ,
,



 ,
где
,
где


 ,
,







 ,
,  .
Справедливость утверждений иллюстрируется
рисунком 22.
.
Справедливость утверждений иллюстрируется
рисунком 22.





 попарно несовместных и образующих
полную группу событий (рис.27), то
вероятность события
определяется по формуле
полной вероятности:
попарно несовместных и образующих
полную группу событий (рис.27), то
вероятность события
определяется по формуле
полной вероятности:



 ,
,

 .
.


