2.5 Параметрические уравнения прямой

Преобразуем уравнения (10)

Рассмотрим каждое уравнение отдельно и выразим соответственно x, y, z.

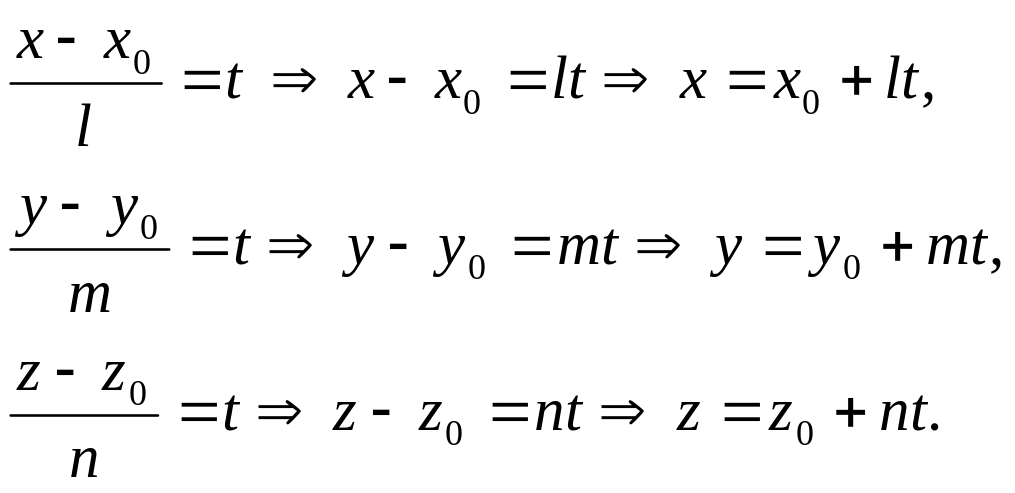
Полученные уравнения: называются параметрическими уравнениями прямой, которые можно записать:

(11)

Задача 11 Канонические уравнения прямой записать параметрическими уравнениями.

Решение

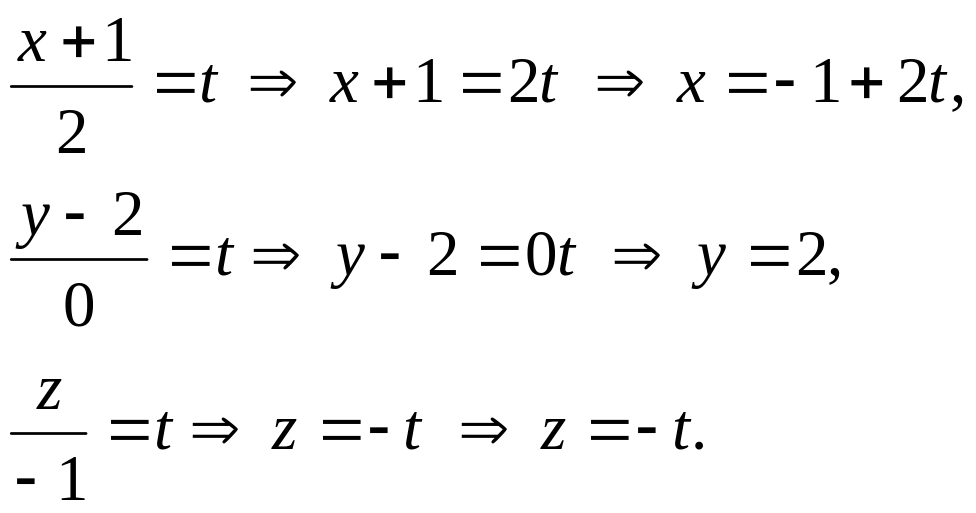
Замечание. Обратите внимание, что если даны канонические или параметрические уравнения прямой, то всегда известны координаты точки, через которую проходит прямая и координаты направляющего вектора.

Для прямых:

l₁:

Записать координаты точки, через которую проходит прямая и координаты направляющего вектора.

Решение

2.6 Уравнение прямой, проходящей через две точки

^{Рассмотрим условие у с л о в и е 2, воспользуемся общим алгоритмом составления уравнения линии.}

1. Дано:

(М₁, М₂)∊l

Составить уравнение прямой l

2 Выполним схематичный чертёж (рис. 15).

Рис.15

2 Возьмем на прямой l произвольную точку M(x,y,z).

4 Составим математическую модель задачи.

Точки M₁, M₂, M₃ принадлежат прямой, тогда векторы и также принадлежат прямой l: значит M₁M ⃦ M₁M₂. Запишем условие параллельности в векторной форме

t: M₁M=t M₁M₂ (#)

5 Запишем уравнение (#) в координатной форме:

,

т.к. вектора параллельные, то их координаты пропорциональные, тогда

(12)

Уравнение (12) называется уравнением прямой, проходящее через две точки.

Задача 12 Составить уравнение прямой, проходящей через две заданные точки и

Решение

Так как даны две точки, воспользуемся уравнением (12)

Подставим координаты точек А и В в составленное уравнение, получим

;

.

Замечание. Обратите внимание, что прямая в пространстве чаще всего записывается каноническими уравнениями.

2.7 Решение задач на составление уравнений прямой в пространстве

Для того что бы составить уравнение прямой в пространстве необходимо:

1 Найти точку, через которую проходит прямая

2 Установить или найти координаты направляющего вектора

3 Составить уравнение прямой, используя уравнение (10).

Задача 13 Составить уравнения прямой, проходящей через точку пересечения плоскости

с осью OX, перпендикулярно плоскости .

Дано:

α₁: ,

α₁∩OX=P, P∊l

α₂:

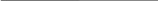
Составить уравнение прямой l.

Решение

1 Найдем точку, через которую проходит прямая.

α₁∩OX=P, тогда P(x,0,0), подставим в уравнение α₁ получим:

, x=6, тогда P(3;0;0).

2 Найдем направляющий вектор прямой.

Выполним схематично чертеж второго условия задачи (рис. 16).

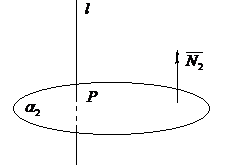
Рис.16

Так как прямая l перпендикулярна плоскости α₂, то нормальный вектор плоскости можно рассматривать как направляющий вектор прямой, т. е. ;

3 Составим каноническое уравнение прямой

,

Ответ:

Задача 15 В треугольнике АВС: А(1;-2;4), В(3;1;3), С(5;1;-7). Составить каноническое уравнение высоты из вершины В.

Решение

Через три точки А, В, С проходит плоскость α и при том только одна,

поэтому ΔАВС лежит в плоскости α.

Выполним схематичный чертеж (рис.17)

N

В

А

S

С

D

Рис.17

1 Найдем точку через которую проходит прямая ВD.

По условию прямая BD проходит через точку В(3;1;3)

2 Найдем координаты направляющего вектора S.

Пусть вектор лежит на прямой BD (рис. 3). По условию

Вектор лежит в плоскости α, тогда – нормальный вектор плоскости.

Если , то вектор можно найти, как векторное произведение векторов

и , т.е. (*)

Найдем вектор :

Найдем координаты векторов :

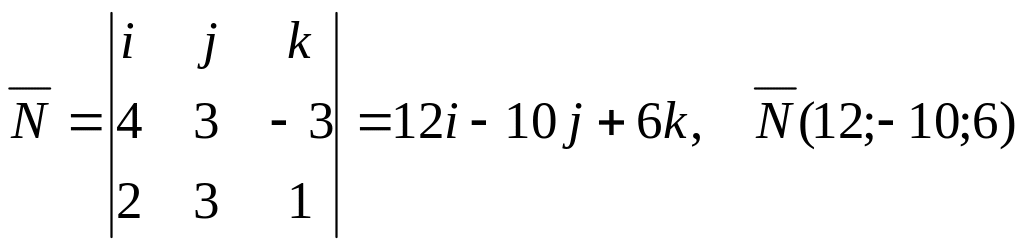
Найдем вектор (см. (*))

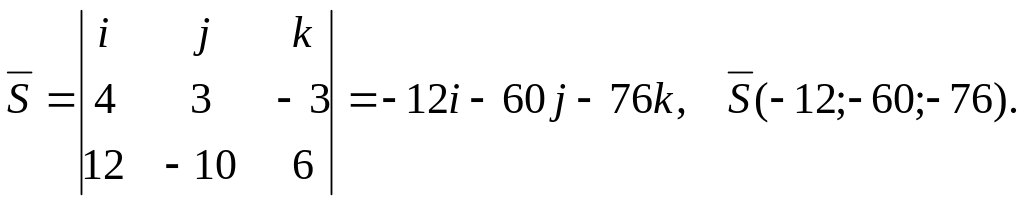
3 Составим уравнение прямой.

Подставим координаты точки Р и вектора в каноническое уравнение прямой, получим уравнение высоты BD:

Помножим каждую часть уравнения на - 4, получим

Ответ: