Раздел 2 Уравнения прямой в пространстве

2.1 Уравнение линии в пространстве

В аналитической геометрии в пространстве каждая линия рассматривается как

пересечение двух поверхностей и соответственно этому определяется заданием двух уравнений.

Например. Окружность в пространстве задается как пересечение сферы:

и плоскости (рис.13)

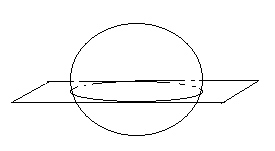
Рис.13

Если и уравнения двух поверхностей, пересекающихся по некоторой линии L, то линия L есть геометрическое место общих точек этих поверхностей, то есть точек координаты которых удовлетворяют одновременно и уравнению и .

Линия в пространстве задаётся в общем случае как линия пересечения некоторых поверхностей и .

Система уравнений:

называется уравнением линии в пространстве.

2.2 Общее уравнение прямой

Если в уравнение линии каждое из уравнений определяет плоскость, то оно определяет прямую в пространстве.

Таким образом прямая в пространстве задается системой уравнений:

(9)

Система уравнений (9) называется общим уравнением прямой в пространстве.

При решении задач общим уравнением пользуются редко. Рассмотрим другие виды уравнений.

2.3 Условия, определяющие прямую в пространстве

^{При решение практических задач использовать общее уравнение прямой достаточно сложно, поэтому более удобным является специальный вид уравнений прямой в пространстве.}

^{По аналогии с прямой на плоскости, прямую в пространстве можно определить условиями:}

^{У с л о в и е 1 Точкой , через которую проходит прямая и вектором параллельным прямой.}

Любой ненулевой вектор, параллельный данной прямой называется направляющим вектором прямой.

Направляющий вектор прямой принято обозначать

У с л о в и е 2 Двумя точками M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂), через которые проходит прямая.

2.4 Уравнение прямой, проходящей через данную точку параллельно данному вектору

^{Рассмотрим условие у с л о в и е 1, воспользуемся общим алгоритмом составления уравнения линии (структурная схема 1)}

^{1 Дано:}

^{S(l,m,n) S ⃦ l}

Составить уравнение прямой l

2 Выполним схематичный чертёж (рис. 14).

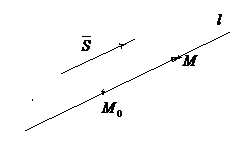
Рис.14

3 Возьмем на прямой l произвольную точку M(x,y,z).

4 Составим математическую модель задачи.

Точка M₀∊ l по условию, точка M∊ l согласно алгоритму, тогда вектор

лежит на прямой l.

По условию задачи S ⃦l, значит S ⃦ . Запишем условие параллельности

векторов в векторной форме:

5 Запишем полученное уравнение в координатной форме, используя условия параллельности векторов в координатной форме.

Найдем координаты вектора :

,

т.к. вектора параллельные, то их координаты пропорциональные, тогда

(10)

Полученные уравнения (10) называют каноническими уравнениями прямой.

Задача 10 Составить уравнение прямой проходящей через точку параллельно вектору .

Решение

1 Установим точку, через которую проходит прямая : .

2 Найдем направляющий вектор S.

Так как вектор ⃦ l, то его можно рассматривать как направляющий вектор прямой, т.е. , тогда .

3 Составим уравнение прямой, используя канонические уравнения прямой (10):

, Получим

.

Ответ: