1.6 Уравнение плоскости в «отрезках»

Замечание Уравнение плоскости в «отрезках», получается преобразование общего уравнения плоскости, аналогично как преобразуется общее уравнение прямой к уравнению прямой в «отрезках». Выполните самостоятельно.

, (3)

где а, b, с - отрезки, которые плоскость отсекает на осях координат, «знак» указывает направление.

Построить плоскость .

Решение

1 Данная плоскость проходит параллельно оси ОZ (таблица 1, п.3.3)

2 Запишем уравнение данной плоскости в «отрезках»:

Выполним почленное деление на 12, получим

на оси ОХ плоскость отсекает отрезок равный 6 в положительном направлении, на оси ОУ

плоскость отсекает отрезок равный 4 в положительном направлении.

3 Выполним построение (рис.4)

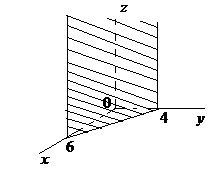
Рис.4

Найти отрезки, которые плоскость отсекает на осях координат.

Решение

Запишем уравнение плоскости в «отрезках»

выполним почленное обеих частей уравнения деление на 12, получим

.

На оси ОХ отсекается отрезок в положительном направлении, на оси ОУ отрезок в отрицательном направлении, на оси ОZ отрезок в положительном направлении.

1.7 Уравнение плоскости, проходящей через три точки

1 Дано:

,

(М₁,М₂,М₃) α

______________________

Составить уравнение плоскости α

2 Выполним схематичный чертёж (рис. 5).

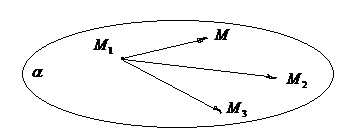
Рис.5

3 Выберем произвольную точку М(х,у,z) принадлежащую плоскости α.

4 Составим математическую модель задачи

Точки , , , принадлежат плоскости, тогда векторы: ( обратите внимание, что вектора рассматриваются из одной точки М₁) также лежат в одной плоскости по аксиоме: если две точки прямой лежат в плоскости, то все точки прямой лежат в плоскости. Если три вектора лежат в одной плоскости, то они компланарные ( по определению).

Если вектора компланарные, то их смешанное произведение равно нулю, тогда имеем:

( ) = 0 (***).

Получили уравнение плоскости в векторной форме.

5 Запишем, полученное уравнение (***) плоскости в координатной форме.

Найдем координаты векторов: , ,

.

Запишем смешанное произведение в координатной форме

= 0 (4)

Задача 2 Составить уравнение плоскости, проходящей через три точки: А(1, -6, 7),

В(4,5,-3) и С(3,0,2).

Решение

Используя уравнение (4) , запишем искомое уравнение в виде:

= 0

Подставим координаты точек, получим

= 0

Выполним вычисления, получим

= 0

Разложим определитель по элементам первой строки, получим

Приведем уравнение к общему уравнению плоскости

Ответ:

Основные уравнения плоскости представлены в структурной схеме 1

Условия, определяющие плоскость

плоскость

1.8 Взаимное расположение плоскостей. Угол между плоскостями

Взаимное расположение плоскостей определяется их нормальными векторами.

Пусть , заданы своими общими уравнениями:

18.1 Условие параллельности плоскостей

Рис.6

Если , то (рис.6). Запишем условие параллельности векторов: - в векторной форме: - в координатной форме: (5)

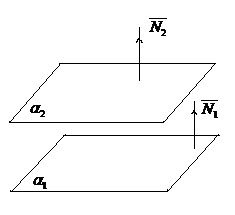
1.8.2 Условие перпендикулярности плоскостей

Рис.7

Если , то (рис.7). Запишем условие перпендикулярности векторов: в векторной форме: в координатной форме: (6)

1.8.3 Угол между плоскостями

Угол между плоскостями определяется углом между их нормальными векторами

(7)

1.9 Расстояние от точки до плоскости

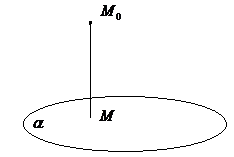Рис.8

Расстояние от точки до плоскости (рис.8) равно длине перпендикуляра и вычисляется по формуле (8)

Замечание Высота многогранника в аналитической геометрии находится как расстояния от вершин многогранника до его основания по формуле (8)

Замечание Расстояние между параллельными плоскостями находится как расстояние от некоторой точки, лежащей на одной из плоскостей, до другой плоскости. В качестве точки, лежащий на одной из плоскостей, рассматривается точка пересечения этой плоскости с одной из осей координат.

Задача 3 Найти расстояние между параллельными плоскостями

Решение

Рассмотрим плоскость , т.к. коэффициенты при неизвестных отличны от нуля и , то она пересекает координатные оси.

Возьмём в качестве некоторой точки плоскости, точку пересечения её с осью OY: .

Подставив координаты точки в уравнение плоскости , имеем:

Тогда

Ответ: