Раздел 1 Плоскость
В этом разделе рассмотрим уравнения плоскости. Для составления уравнений плоскости будем использовать общую структуру составления уравнений линий (поверхностей) (структурная схема 1)
Структурная схема составления уравнения линии (поверхности)
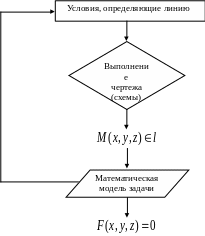
Структурная схема 1
1.1 Уравнение поверхности
Уравнение
называется уравнением поверхности,
если координаты каждой точки лежащей,
на поверхности ему удовлетворяют, а
координаты точки не лежащей, на поверхности
не удовлетворяют.
Если в уравнение переменные x,у,z содержатся в первой степени, то оно определяет поверхность первого порядка (плоскость). Если хотя бы одна из переменных содержится во второй степени, по поверхность второго порядка и т.д.
1.2 Условия определяющие плоскость в пространстве
Плоскость принято обозначать греческими буквами: α, β, γ и т.д. На рисунках плоскость изображается в виде параллелограмма (рис.1) или произвольной ограниченной области (рис.2).
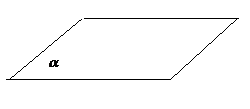
Рис.1
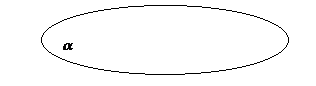
Рис.2
У
с л о в и е 1 Плоскость в пространстве
однозначно определяют точка
и вектор
перпендикулярный данной плоскости.
Вектор перпендикулярный плоскости называется нормальным вектором плоскости и обозначается .
У
с л о в и е 2 Исходя из аксиомы
стереометрии: через любые три точки,
не лежащие на одной прямой, проходит
плоскость и притом только одна, можно
утверждать, что три точки:
,
,
не лежащие на одной прямой определяют
в пространстве плоскость и притом только
одну.
Рассмотрим следствия из аксиом, которые так же однозначно определяют плоскость в пространстве.
У с л о в и е 3 Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
У с л о в и е 4 Через две пересекающиеся прямые проходит плоскость, и притом только одна.
У с л о в и е 5 Через две параллельные прямые проходит плоскость, и притом только одна.
Условия 3-5 будут рассмотрены после изучения уравнения прямой в пространстве
1.3 Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору ( условие 1)
1 Дано:
__________________________________
Составить уравнение плоскости α.
2 Выполним схематичный чертёж (рис. 3).
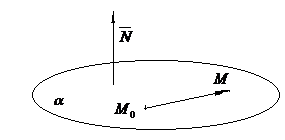
Рис.3
3 Выберем произвольную
точку
принадлежащую плоскости
α.
4 Составим математическую модель задачи
Рассмотрим вектор
,
по аксиоме: если две точки прямой лежат
в плоскости, то все точки прямой лежат
в плоскости, можно утверждать, что
вектор
лежит
в плоскости α. По
условию
,
значит он перпендикулярен любой
прямой, лежащей в плоскости α,
т.е.
.
Запишем условие перпендикулярности
векторов в векторной форме
(*)
Получили уравнение плоскости в векторной форме.
5 Запишем, полученное уравнение (*) плоскости в координатной форме.
Найдем координаты вектора :
.
Запишем скалярное произведение векторов в координатной форме:
(1)
где А,В,С – координаты нормального вектора
Полученное уравнение (1) плоскости называется уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору.
Замечание Уравнение (1), является основным уравнением плоскости, которое используется для решение практических задач.
Для того что бы составить уравнение плоскости в пространстве необходимо:
Определить (найти) точку, через которую проходит плоскость.
2 Найти нормальный вектор плоскости.
Нормальный вектор плоскости чаще всего находится как векторное произведение векторов, ему перпендикулярных. Эти векторы определяются из условия задачи.
3 Составить уравнение плоскости по уравнению (1).