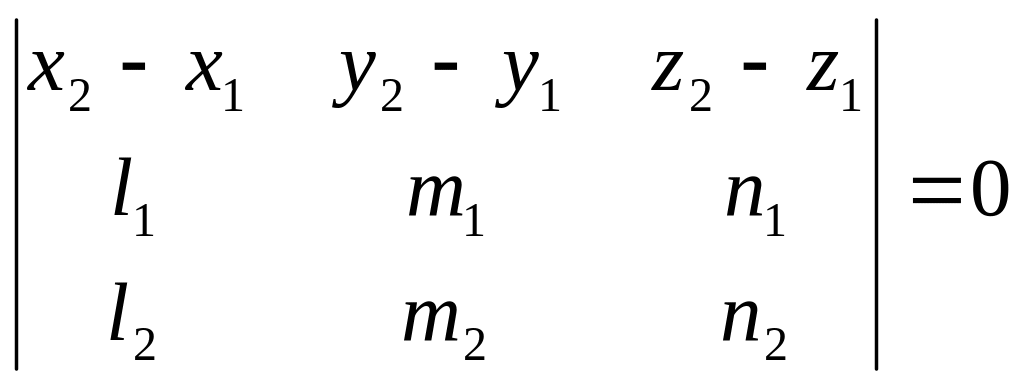Уравнение искомой плоскости будем искать по формуле: (*), где
По условию
,
,
значит
Из
уравнения плоскости
имеем
,
из уравнения прямой
.
Тогда
,
.
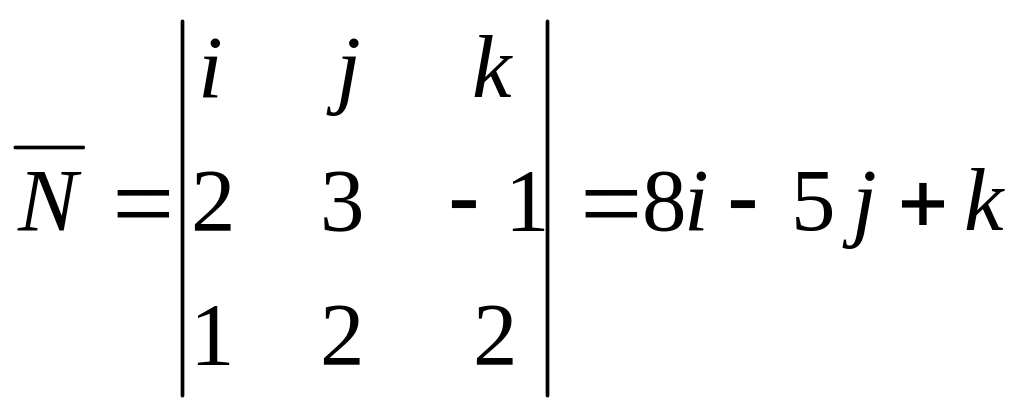Подставим
координаты вектора
и точки
в уравнение (*).
или
Ответ:
Задача 28 Найти расстояние между скрещивающимися прямыми:
, .
Решение
Расстояние между
скрещивающимися прямыми найдём как
расстояние от точки
,
до плоскости
,
проходящей через прямую
параллельно прямой
.
Уравнение плоскости
составим по формуле:
(*).
Вектор
,
т.к.
,
,
т.к.
,
тогда
.
Из уравнения прямой
имеем:
,
аналогично
.
подставим в
уравнение (*) координаты вектора
и точки
.
Найдём
Ответ:
3.6 Задачи для самостоятельного решения
Задача 29 Найти проекцию точки на плоскость, проходящую через параллельные прямые:
, ; ; .
Ответ:
Задача 30 Доказать, что прямые ; ; и ; ; лежат в одной плоскости и составить её уравнения.
Ответ:
Задача 31 Найти проекцию точки на прямую ; ; .
Ответ:
Задача
32 Составить уравнение плоскости,
проходящей через точку
,
перпендикулярно к прямой
Ответ:
Задача 33 Составить уравнение плоскости, проходящей через начало координат, параллельно прямой и перпендикулярно к плоскости .
Указание.
Так как искомая плоскость
параллельна прямой
,
то её нормальный вектор
будет перпендикулярен вектору
прямой. Из условия, что плоскость
перпендикулярна плоскости
,
следует что
будет перпендикулярен
,
тогда
.
Ответ:
Задача
34 Составить уравнение плоскости,
проходящей через прямую
;
;
параллельно прямой
Ответ:
Задача 35 Составить уравнение прямой, проходящей через точку пересечения прямой с плоскостью и точку .
Ответ:
Задача 36 Составить уравнение прямой, проходящей через проекцию точки на плоскость и точку пересечения данной плоскости с осью OY.
Ответ:
Задача
37 Найти расстояние от точки
до плоскости, проходящей через
;
;
и параллельно прямой
Ответ:
Задача 38 Написать уравнение перпендикуляра, опущенного из точки на прямую
Приложение а Базовые уравнения, формулы и понятия
Таблица 3
№ |
Базовые уравнения, формулы и понятия
|
Аналитический вид уравнений, формул и понятий |
1 |
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору («основное») |
|
2 |
Общее уравнение плоскости |
,
где А, В, С координаты нормального
вектора
,
|
3 |
Уравнение плоскости в «отрезках» |
|
4 |
Уравнение плоскости, проходящей через три точки: А, В, С. |
= 0 |
5 |
Взаимное расположение плоскостей:
|
|
5.1
|
Условие параллельности плоскостей в векторной форме |
|
5.2 |
Условие параллельности плоскостей в координатной форме |
|
5.3 |
Условие перпендикулярности плоскостей в векторной форме |
|
5.4 |
Условие перпендикулярности плоскостей в координатной форме |
|
6 |
Угол между плоскостями |
|
7 |
Расстояние от
точки
до плоскости
: |
|
8 |
Общее уравнение прямой |
|
9 |
Канонические уравнения прямой |
|
10 |
Параметрические уравнения прямой |
|
11 |
Уравнения прямой,
проходящей через две точки
|
|
,
и
Окончание таблицы 3
12 |
Взаимное расположение прямых:
|
|
12.1 |
Условие параллельности прямых в векторной форме |
|
12.2 |
Условие параллельности прямых в координатной форме |
|
12.3 |
Условие перпендикулярности прямых в векторной форме |
|
12.4 |
Условие перпендикулярности прямых в координатной форме |
|
12.5 |
Условие пересечения прямых в векторной форме |
|
12.6 |
Условие пересечения прямых в координатной форме |
|
13 |
Взаимное
расположение прямой
и
плоскости
|
|
13.1 |
Условие параллельности прямой и плоскости в векторной форме |
|
13.2 |
Условие параллельности прямой и плоскости в координатной форме |
|
13.3 |
Условие перпендикулярности прямой и плоскости в векторной форме |
|
13.4 |
Условие перпендикулярности прямой и плоскости в координатной форме |
|
13.5 |
Условие принадлежности прямой плоскости в координатной форме |
|
