3.3 Уравнение плоскости, проходящей через прямую и точку, не принадлежащую данной прямой

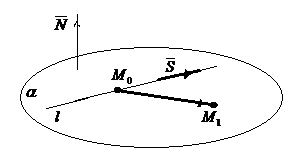
АЛГОРИТМ 7 Уравнение плоскости, проходящей через прямую и точку, не принадлежащую данной прямой Дано: ________________________________ Составить уравнение плоскости α: Решение Выполним схематичный чертеж (рис. 23) Рис.23 1 2 Найдем нормальный вектор плоскости α (рис. 23): Нормальный вектор плоскости N как векторное произведение векторов: 3 Подставим координаты точки и вектора в «основное» уравнение (1) плоскости, получим

Задача 25 Составить уравнение плоскости, проходящей через точку и прямую

Решение

1

2 Найдем нормальный вектор плоскости α (рис. 32):

Нормальный вектор плоскости N найдем как векторное произведение векторов:

3 Подставим координаты точки и вектора в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору , получим

Ответ:

Выполните самостоятельно

Задача 25.1 Найти расстояние от точки до плоскости, проходящей через прямую и точку

Ответ: точка М лежит в плоскости

3.4 Взаимное расположение прямой и плоскости в пространстве

Прямая и плоскость в пространстве могут пересекаться, быть параллельными или прямая лежит в плоскости.

Пусть прямая задана каноническими уравнениями: , а плоскость своим общим уравнением:

Структурная схема 4

3.5 Угол между прямыми, между прямой и плоскостью

Угол между прямыми определяется углом между их направляющими векторами

(13)

Угол между прямой и плоскостью определяется как угол между направляющим вектором прямой и нормальным вектором плоскости по формуле:

(14)

3.6 Решение задач на прямую и плоскость

Задача 26 Составить уравнение прямой, которая проходит через точку перпендикулярно вектору и пересекает прямую .

Решение

Искомая прямая пересекает данную прямую , значит, через них проходит плоскость . Найдём нормальный вектор плоскости .

, ,

Нормальный вектор плоскости будет перпендикулярен , т.к. и вектору , т.е. .

Направляющий вектор искомой прямой перпендикулярен вектору по условию и вектору , т.к. , тогда:

,

,

.

Составим канонические уравнения прямой :

умножим полученное на (–29):

Ответ:

Задача 27 Написать уравнение плоскости, проходящей через точку , перпендикулярной плоскости и параллельной прямой .

Решение