Приложение b

(информационное)

Библиография

[1] Инструкция по подготовке, оформлению и представлению к защите дипломных работ в высших учебных заведениях. Утверждена приказом Министра образования Республики Беларусь от 27.06.1997 №365.

[2] Положение о государственных экзаменационных комиссиях в высших учебных заведениях Республики Беларусь от 27.06.1997 №365.

Раздел 1

Используя логическую функцию ЕСЛИ и встроенные

математические функции, построить таблицу и график значений функции на отрезке [0,1] с шагом 0,05.

1.

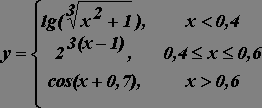
2.

3.

4.

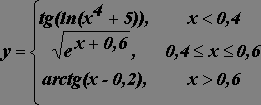
5.

6.

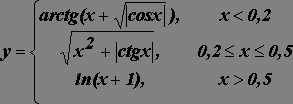
7.

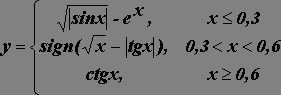
8.

9.

10.

11.

12.

13.

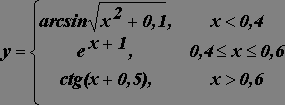
14.

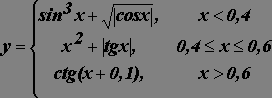
15.

Раздел 2

Используя инструмент Подбор параметра, найти корни уравнения, корни предварительно локализовать графически.

Варианты

1. на отрезке [-1;1,3]; табуляцию произвести с шагом 0,1.

2. на отрезке [-2;20]; табуляцию произвести с шагом 1. на отрезке [-1;1]; табуляцию произвести с шагом 0,1.

3. на отрезке [-13;7]; табуляцию произвести с шагом 0,8.

4. на отрезке [-1;3]; табуляцию произвести с шагом 0,2.

5. на отрезке[-22;20]; табуляцию произвести с шагом 2.

6. на отрезке [0;8]; табуляцию произвести с шагом 0,4.

7. на отрезке [4;12]; табуляцию произвести с шагом 0,4.

8. на отрезке [-12;0]; табуляцию произвести с шагом 0,6.

9. на отрезке [-18;20]; табуляцию произвести с шагом 2.

10. на отрезке [-12;0]; табуляцию произвести с шагом 0,5.

11. на отрезке [-1;10]; табуляцию произвести с шагом 0,5.

12. на отрезке [-6;17]; табуляцию произвести с шагом 1.

13. на отрезке [-15;25]; табуляцию произвести с шагом 2.

14. на отрезке [-12;24]; табуляцию произвести с шагом 2.

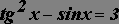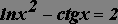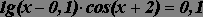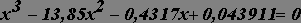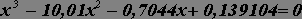15. на отрезке[0;1,5]; табуляцию произвести с шагом 0,1._.

Раздел 3

В соответствие с вариантом найти решение X системы линейных алгебраических уравнений AX=B, где A - матрица коэффициентов; B - вектор свободных членов. В матричной алгебре решение системы находится как X=A^-1B, где A^-1 - обратная матрица.

Варианты заданий

Задания определены общей для всех вариантов матрицей A и различными векторами B, показанными в таблице.

Матрица A

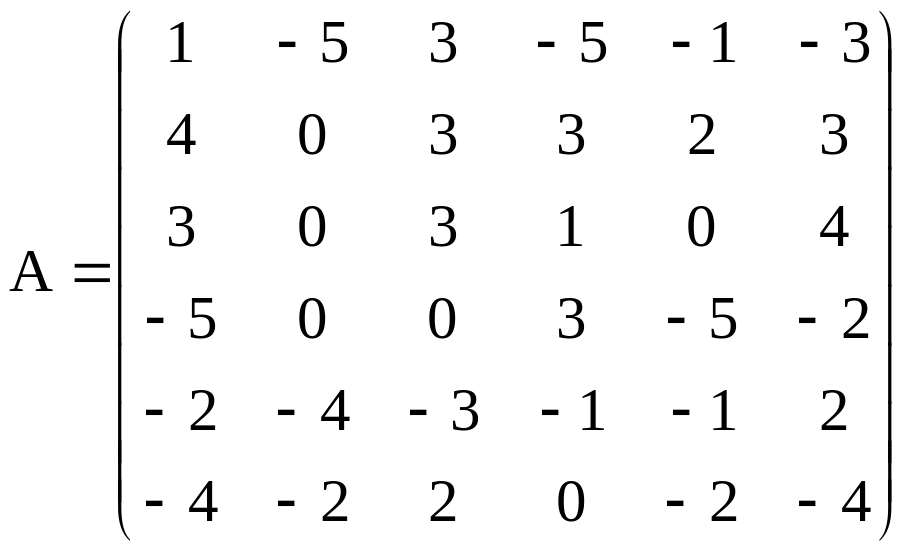
Вектор B

№	b1	b2	b3	b4	b5	B6		№	b1	b2	b3	b4	b5	b6
1	-21	10	10	22	-11	4		16	34	68	89	-49	-43	-48
2	10	24	21	35	-55	40		17	-13	24	44	-54	3	-84
3	-46	6	1	12	-18	-8		18	-40	48	29	-89	-28	-90
4	-27	6	10	27	-10	-4		19	-92	23	9	-51	-47	-78
5	-29	7	10	22	-9	-10		20	-33	46	36	-64	-91	-48
6	-28	17	5	-9	-21	-18		21	15	63	59	-87	-73	-60
7	7	15	12	-29	-27	-16		22	-84	34	36	-32	-45	-82
8	12	9	10	-35	-29	-18		23	-65	34	32	-24	-69	-60
9	4	2	3	-28	-37	-14		24	-92	41	43	-24	-59	-80
10	1	0	-7	-21	-44	-8		25	-96	48	47	-26	-62	-84
11	-35	57	44	-55	-44	-50		26	-76	30	10	-26	-99	-50
12	-46	43	24	-91	-22	-80		27	-93	20	1	-21	-99	-54
13	0	20	3	-48	-48	-28		28	-90	39	45	-16	-99	-64
14	18	9	-1	-65	-43	-34		29	-79	37	46	-27	-99	-68
15	18	67	72	-16	-57	-24		30	-76	37	49	-22	-99	-68