3 Механические характеристики производственных механизмов и электродвигателей

Основной функцией электропривода является приведение в движение рабочей машины в соответствии с требованиями технологического режима. Движение это совершается механической частью электропривода (МЧ ЭП), в состав которой входит ротор электродвигателя, передаточное устройство и рабочая машина (рис. 3.1). Приведенные на рис. 3.1 параметры обозначают М_в, М_рм, М_ио – моменты на валу двигателя, рабочей машины, исполнительного органа; ω_в, ω_рм , ω_ио – угловые скорости вала ЭД, рабочей машины, исполнительного органа; F_ио, V_ио – усилие и линейная скорость исполнительного органа. В зависимости от вида передачи и конструкций рабочей машины различают (рис. 3.1):

1. 􀂾ЭП вращательного движения, обеспечивающий, соответственно, вращательное движение исполнительного органа РМ; выходные параметры – момент ИО механизма М_ио и угло-вая частота вращения ω_ио;

2. 􀂾ЭП поступательного движения, обеспечивающий поступательное линейное движение ИО рабочей машины; выходные параметры – усилие F_ио и линейная скорость V_ио.

Рисунок 3.1

Отметим, что существует также специальный ЭП, называемый колебательным электроприводом, обеспечивающим возвратно-поступательное (вибрационное) движение (как угловое, так и линейное) исполнительного органа РМ.

В механической части ЭП действуют различные виды усилий, моментов, различающиеся характером действия. Различают статические моменты реактивные М_ср и активные М_са.

Реактивные моменты создаются силой трения, силами сжатия, растяжения, кручения неупругих тел. Классическим примером здесь может служить сухое трение (рис. 3.2). Силы трения всегда противодействуют движению и при реверсе электропривода момент трения, обусловленный этими силами, также меняет направление, а функция М_с(ω) при скорости ω = 0 претерпевает разрыв. Силы трения проявляются в передачах электродвигателя и рабочих машинах.

Активные (потенциальные) моменты создаются силой тяжести, силами сжатия, растяжения, кручения упругих тел. В МЧ ЭП активные моменты возникают в нагруженных элементах (валы, зубчатые зацепления и т.п.) при их деформации, поскольку механические связи не являются абсолютно жесткими. Особенности действия потенциальных моментов наглядно проявляются на примере силы тяжести. При подъеме или спуске груза направление силы тяжести F_j остается постоянным. Иными словами, при реверсе электропривода направление активного момента М_са сохраняется неизменным (рис. 3.3).

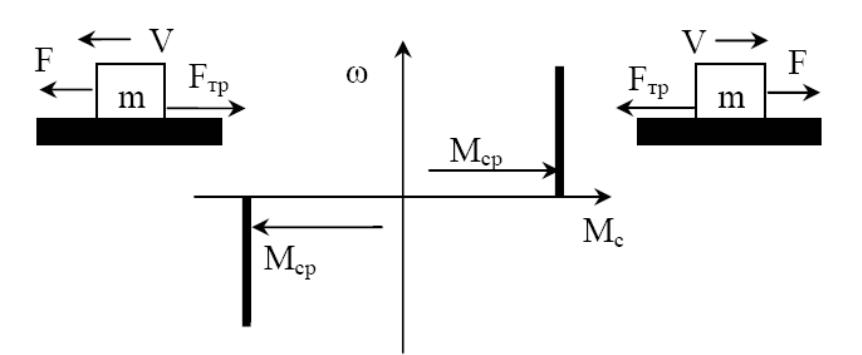
Рис. 3.2. Зависимость статического момента сил сухого трения от скорости

Краткий анализ видов М_с показывает, что между реактивными и активными моментами имеется существенное отличие: реактивный момент с изменением направления движения также меняет свое направление, активный же момент сохраняет его постоянным.

Рабочие машины, несмотря на большое многообразие конструкций и выполняемых операций, могут быть классифицированы по виду зависимости статического момента от ряда факторов. Можно выделить следующие основные группы механизмов.

К первой группе относятся механизмы, у которых статический момент не зависит от скорости вращения, то есть М_с(ω) = const. Это значит, что механическая характеристика рабочей машины – зависимость статического момента от частоты вращения – представляет прямую, параллельную оси угловой скорости ω, и претерпевает разрыв при ω = 0 для реактивных статических моментов (как показано на рис. 3.2), например, для ленточного транспортера с равномерной погонной нагрузкой.

Рис. 3.3. Зависимость активного статического момента от скорости, характерная для механизмов подъема грузов

Для активных М_с (как показано на рис. 3.3) механическая характеристика не зависит от направления движения. Типичным примером является механизм подъемника.

Вторая группа механизмов достаточно представительна. Здесь М_с зависит от скорости вращения РМ:

М_С(ω) = М_С0 + (М_СН + М_С0) (ω / ω_н)^а

(3.1)

где М_со – момент механических потерь на трение;

М_сн – статический момент рабочей машины при номинальной скорости вращения ω_н;

ω – текущая скорость вращения;

а – коэффициент пропорциональности.

При а = 0 имеем М_с(ω) = М_сн, то есть получаем механическую характеристику машин первой группы.

При а = 1 имеем линейную зависимость статического момента от скорости, что присуще, например, генераторам G постоянного тока, работающим на постоянное сопротивление R (рис. 3.4).

При а = 2 (рис. 3.5) получаем наиболее многочисленную группу рабочих механизмов], имеющих вентиляторную характеристику (вентиляторы, гребные винты, центробежные насосы и другие подобные механизмы).

При а = -1 имеет место гиперболическая зависимость, характерная для большинства металлорежущих станков, когда с увеличением скорости подачи резца V (соответственно при этом увеличивается усилие резания) снижает скорость обработки детали ω (рис. 3.6).

Отметим, что на практике встречаются и другие значения коэффициента а.

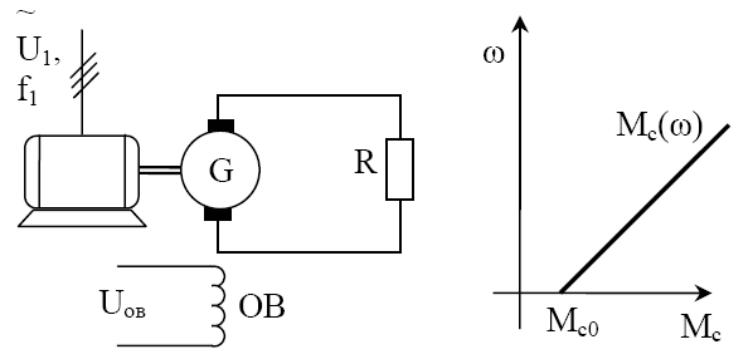
Рис. 3.4. Механическая характеристика при а = 1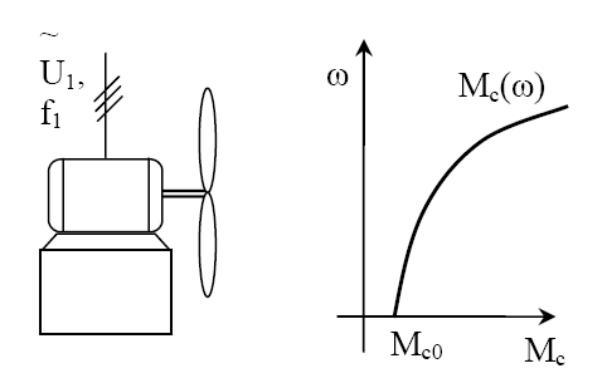

Рисунок 3.5 Вентиляторная механическая характеристика

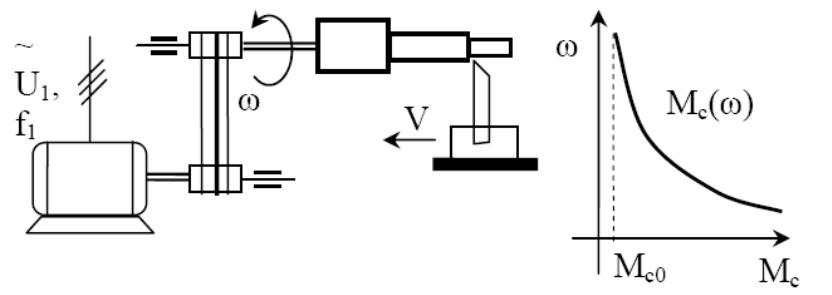
Рис. 3.6. Гиперболическая механическая характеристика

Механические характеристики электродвигателей

Прежде чем перейти к рассмотрению характеристик электродвигателей, дадим некоторые определения.

Механическими характеристиками двигателя называются зависимости установившейся частоты вращения от вращающего момента ω = f(M).

Электромеханическими характеристиками двигателя называются зависимости установившейся частоты вращения от тока – ω = f(I).

Характеристики называют естественными, если они получены при номинальных условиях питания (при номинальных напряжении и частоте вращения), номинальном возбуждении и отсутствии добавочных сопротивлений в цепи якоря. Характеристики двигателя называются искусственными при изменении любого из перечисленных выше факторов.

Для вывода электромеханической и механической характеристик двигателя постоянного тока с независимым возбуждением рассмотрим простейшую схему включения двигателя (рисунок 3.9).

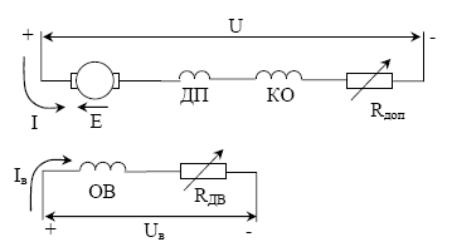
Рисунок 3.7- Схема электрическая принципиальная двигателя постоянного тока независимого возбуждения

К якорю электродвигателя прикладывается напряжение сети постоянного тока U_c = U, которое в установившемся режиме уравновешивается ЭДС (Е) двигателя и падением напряжения в цепи якоря (I_я·R_яц).

U = Е + I_я·R_яц , (3.2)

где R_яц = R_я + R_доп + R_дп + R_ко – полное сопротивление цепи якоря, Ом;

R_я – сопротивление обмотки якоря, Ом;

R_доп – добавочное сопротивление в цепи якоря, Ом;

R_дп , R_ко – соответственно, сопротивления обмоток дополнительных полюсов и компенсационной обмотки, Ом;

Е = КФω – ЭДС двигателя

КФ(С)-величина, характеризующая магнитный поток двигателя

Подставив в уравнение (4.1) значение Е и произведя соответствующие преобразования относительно частоты вращения ω, получим электромеханическую характеристику электродвигателя постоянного тока независимого возбуждения

(3.3)

Выразив величину тока якоря через электромагнитный момент М=КФI и подставив значение тока в уравнение (4.2), найдем механическую характеристику двигателя постоянного тока с независимым возбуждением:

(3.4)

А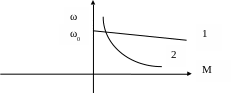 нализируя уравнения (3.3) и (3.4), видим, что математически это уравнения прямой линии, пересекающей ось скоростей в точке ω ₀ (рисунок 3.8-1). Величина ω₀ = U/(К·Ф) – называется скоростью идеального холостого хода.

Рисунок 3.8- Механическая характеристика двигателя постоянного тока независимого (параллельного ) возбуждения

Для двигателя постоянного тока последовательного возбуждения (рисунок.3.8-2)

Для асинхронного электродвигателя механическая характеристика имеет более сложный вид (рисунок 3.9 -1).

Рисунок 3.9

ω₀ – синхронная скорость;

М_к – максимальный (критический) момент;

М_п- пусковой момент.

Для синхронного электродвигателя вид прямой линии параллельной оси момента (рисунок 3.9-2).

4. Режимы работы электропривода. Регулирование скорости электроприводов

Уравнение движения электропривода

Р ассмотрим простейшую механическую систему, состоящую из вращающейся части двигателя (ротора или статора - РД) и рабочего органа (РО) механизма, имеющего вращательное движение, присоединенного непосредственно к валу двигателя (рисунок 4.1). В системе действуют два момента – момент, развиваемый двигателем М_Д и момент статической нагрузки М_С, в который входят момент, создаваемый рабочим органом механизма и моменты трения. Эти моменты характеризуются величиной и направлением действия. Если М_Д и М_С действуют в направлении движения, их называют движущими, если их знаки противоположны знаку скорости, моменты называют тормозящими. В соответствии с принципом Деламбера, совместное действие М_Д и М_С определит величину и знак динамического момента (J-момент инерции), определяющего ускорение системы. Таким образом, уравнение движения системы в общем случае имеет вид

. (4.1)

Проведем простейший анализ уравнения (4.1) для двигательного режима работы ЭП, когда

. (4.2)

При М_Д > М_С dω/dt > 0 имеет место режим ускорения привода, при М_Д < М_С dω/dt < 0 и имеет место режим замедления привода, а при М_Д = М_С динамический момент и ускорение равны нулю. Первые два режима называют переходными, а последний – установившимся (стационарным).

Работа электродвигателя характеризуется следующими основными величинами:

1. • М – электромагнитный момент, развиваемый электродвигателем, Н·м;

2. •М_c – момент сопротивления (нагрузка, статический момент), создаваемый производственным механизмом, Н·м,

3. • I_я – ток якоря электродвигателя, А;

4. • U – напряжение, приложенное к якорной цепи, В;

5. • Е – электродвижущая сила (ЭДС) машины постоянного тока (для электродвигателя ее называют противоЭДС, так как в электродвигателе она направлена навстречу напряжению U и препятствует протеканию тока);

6. • Ф – магнитный поток, создаваемый в электродвигателе при протекании тока возбуждения по ОВ, Вб;

7. • R_я – сопротивление цепи якоря, Ом;

8. • ω – угловая частота (скорость) вращения якоря

1. • Р – мощность двигателя, Вт.

2. Различают механическую (полезную) мощность на валу двигателя -Р_мех

Р_мех = М · ω , (4.3)

и полную (электрическую) мощность

Р_эл = U · I_я ; (4.4)

Из уравнений электромеханической и механической характеристик электродвигателя постоянного тока с независимым возбуждением:

; ,

где С = кФ , следует, что возможны три основных способа регулирования угловой скорости (см. рисунок 4.1):

а) изменением напряжения U_Я, подводимого к якорю;

б) изменением сопротивления цепи якоря двигателя переменным добавочным резистором R_Д;

в) изменением тока возбуждения I_В (воздействие на величину магнитного потока, коэффициент - С).

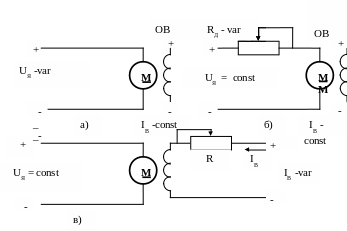
Рисунок 4.1-Схемы включения электродвигателя для основных способов регулирования.

Вид типичных электромеханических и механических характеристик, полученных в этих схемах регулирования, представлен на рисунке 4.2.

Рисунок 4.2- Механические и электромеханические характеристики для трех способов регулирования: а) регулирование напряжением на якоре двигателя; б) регулирование добавочным резистором в цепи якоря; в) и г) регулирование током возбуждения, электромеханические и механические.

Принцип частотного регулирования скорости АД и СД

Скорость вращения ротора асинхронной и синхронной машин зависит от частоты питающей сети. При этом синхронная скорость ( когда скорость вращения ротора равна скорости вращения поля статора) определяется известной формулой

или

где f - частота питающей сети;

р – число пар полюсов конкретного электродвигателя;

ω₀ - скорость вращения в рад/сек;

n₀ - тоже в об/мин.

Отсюда легко определяется синхронная скорость при известной частоте сети. Так, если f = 50 Гц то при одной паре полюсов n₀ = 3000 об/мин, две пары n₀ = 1500 , 3р n₀ = 1000 и тд. На рисунке 1 приведен пример механических характеристик АД и СД при двух частотах f₁ и f₂.

n

СД

n₀

АД

n₀₁

Рисунок 4.3

Понятно, что если мы будем менять частоту сети то будет и регулироваться скорость двигателя. При снижении частоты сети и неизменном напряжении начнет возрастать ток двигателя. Очевидно, что необходимо одновременно снижать и напряжение на двигателе, в тоже время, учитывая характер нагрузки. Эти вопросы решены основоположниками частотного регулирования ( Костенко и др.). Получены формулы законов частотного регулирования для различных типов механизмов .

1. Для механизмов с постоянным моментом нагрузки отношение напряжения статора к частоте для всего диапазона регулирования должно оставаться постоянным

U / f = const

2. Для механизмов с вентиляторной нагрузкой (турбо-механизмы) этот закон выражается следующей формулой

U / f² = const

В частотно- регулируемых электроприводах ЧРП, система управления предусматривает реализацию заданного закона управления.