28 Конечно-разностная схема. Схема Кранка-Никольсона.
При использовании неявной схемы все величины определяются одновременно
=
(1)
Если в явном виде была 1 неизвестная, то для неявного получаем ур-е с 3-мя неизвестными. . Это уравнение содержит члены соответствующие всем неизвестным Значение давления на новом временном уровне.
Умножим (1) на и сгруппируем подобные члены
) +
аiPi-1-biPi+ciPi+1=di. Где аi,bi,ci- Коэфф. учитывающие геометрию системы и её физ. Свойства. Записав данное уравнение для n ячеек линейной сетки и объединив уравнения для каждой ячейки, получим n уравнений с n неизвестными.
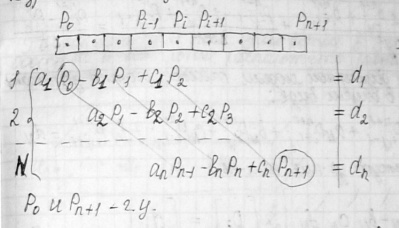
Ячейки с номерами 0 и n+1 фиктивные и в модели они заменяются соответствующим г.у. Данную систему из n уравнений мы можем записать в матричном виде. в матрице имеется 3 диагональных элемента и все элементы, находящиеся на диагонали равны 0. Данная матрица называется 3х диагональной.
[аi-bici]*[Pi]=[di]
Смешанная конечно-разностная схема вычисления значения функции по координате х :
Если Ѳ=0 – схема явная. Если Ѳ=1/2 – схема Кранка-Никольсона
Если Ѳ=1 – схема неявная.
29. Типы сеток. Два способа построения сеток.
1-й способ. Поместить первый и последний узлы сетки в точки х=0 и х=l соответственно, а остальные расположить равномерно м/у ними
Для определения объема блока связанно с каждым узлом поместим границы блоков по середине м/у узлами, тогда объем блока будет равен V=∆x∙a,
где а- площадь сечения;
Такой метод построения сетки называют методом «сетки с распределенными узлами».Для данной сетки получаем, что зависимые параметры вычисляются на пересечении линии сетки на границах блоков значения параметров опр-ся в нескольких точках.
2-й способ. Можно поделить отрезок L на N равных блоков и затем разместить узлы в центрах этих блоков
Блочно-центрированный способ
Для равномерных сеток различие м/у двумя видами сеток заключается в способе представления граничных условий.
Блочно-центрированные сетки обычно используют для граничных условий типа Неймона (граничн. условие второго рода,где задаются первые производные)
Типами Неймана определяется кол-во флюида протекающего через границу, задается градиент давления.
Для способа узлового типа сетки задают граничные условия типа Дерифле (граничное условие 1-го рода)
30. Критерий устойчивости вычислений. Анализ Неймана(Фурье).
Чтобы использовать систему уравнений для определения зависимости переменных при моделировании, ее решения должно быть устойчивым.
Пусть
погрешность между точкой и вычисленным
решением в какой нибудь момент n,
тогда
решение устойчиво;
решение неустойчиво.
Для анализа устойчивости применяют два способа:
анализ Неймона (анализ Фурье)
матричный метод
сначала погрешность конечной разности аппроксимации уравнений выражается в виде конечных рядов Фурье. Затем анализируется рост этой погрешности в процентном решении. Устойчивость схемы решений зависит от того можно ли контролировать величину погрешности и будет ли она достаточно малой во всей области решений.
Разложение функции в ряд Фурье обычно выражается в виде синус или косинус членов, для упражнения принимаем комплекс:
экспоненциальная форма
где
i=
Решение конечно разностных уравнений соответсвует диф. уравн. в частных производных получают в виде диспертного ряда величин.