20. Понятие подземной гидродинамики в моделировании.
Течение
флюидов в поровой среде сложное явление
которое нельзя просто описать мат.
путем, как давл.жидкости по трубам или
течение электронного тока по проводам,
отличие в том что в этом процессе не
существует трубок тока с четко
ограниченным сечением S
которого можно изменить. Для описания
характера течения флюидов в пор среде
искл.понятия К, потенциал V
теч.,
-ий
однородной и многофазной систем.
Закон Дарси. Понятие К .
Vs=-
(ϑ
+
)=
Vs- массовая скорость в направлении потока S. К-проницаемость для однородных флюидов. μ-динамическая вязкость. Р-давление. z-вертикальная координата
V=
–удельный объем. ρ-плотность флюида.
-потенциал ϑфункции флюида. Ф-полный потенциал ϑ-давления флюидов.
Область применения:
а. флюид однородный=однофазный
б. отсутствуют хим. реакций м/у средой и флюидом
в. К-не зависит от типа флюида, t, Р, и пространственных координат
г. Течения ламинарные.
д. отсут-ет электрокинематический эффект.
е. отсут-ет эффект прилипания к стенкам (эффект Линкенберга).
Потенциал скорости течения φ При фильтраций флюидов в кор.среде Vs всегда ортогональны. Эквипотенциальным поверхностям, скалярное их значение пропорционального grad-том этих φ. Для перемещения частицы флюида в определенное положение надо воплотить выполнить работы нескольких видов. Полная сумма всех работ соответствует потенциальной энергий элементарной массы флюидов
Рис.
Распр. Линий равных φ и линий тока.
1-линия тока φ- эквивалентные
поверхности.
Ф=
+ z1+
-изм.положения.
-
ускорение частицы. Т.к.
фильтрации
тела
=0
Если флюид несжимаем V≠f(P) , следует Ф1=V(р1-р1)+z1
21. Стационарное и нестационарное течения. Рассмотрим траекторию движения частицы флюида в пористой среде.
1-траектория движения частицы
2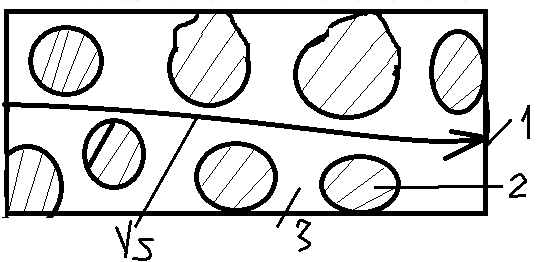
-
порода
3- пористое пространство
-
скорость частицы
Ускорение частицы можно получить путем определения быстроты изменения вектора скорости.
V = f(s,t)
dv=
,
- ускорение в точке,
- конвекционное ускорение
Конвекционное ускорение – определяется при движение вместе с частицей флюида.
=0,
=0
Рассмотрим радиально симметричный пласт с конечными внешними радиусами.
Пласт остается в состоянии равновесия пока на границах не будет приложено некоторое возмущение.
Система может перейти либо в стационарное либо в нестационарное состояние.
Внутренние границы:
1.Постоянное
давление на забое скважины: P(
)=const
2
.Постоянный
дебит: r
= const
3.Переменное давление на забое скважины: P( )= f(t)
4.Переменный
дебит: r
= q(t)
5. Отключ. Скважины.
Внешние границы:
6. Пост. Давление : P( )=const
7. Пост. Переток через границ: = const
8. Перемен. Переток через границ: = f(t)
9. Замкнутая внешняя граница.
10.
Бесконечный пласт. lim
P(
)=
Когда скважина включается, давление вокруг внутреннего радиуса начинает падать и волна снижающегося давления движется к границам пласта. При различных сочетаниях внутренних и внешних границ условно сложно создать область стационарного течения.