4 Принципы составления уравнений в частных производных

Рассмотрим принципы составления уравнений в частных производных применительно движения жидкостей в трубах и пористых средах.

Пусть жидкость движется в трубке радиуса R

Обозначим через U среднюю скорость движения жидкость в направлении оси X.

W=ρU- поток массы ч/з ед. площади сечения и если жидкость сжимаема то масса жидкости м/у сечениями 1 и 2 меняется за время Δt на величину:

ΔM=W'SΔt-W''SΔt=-ΔWSΔt

ΔM=ΔρSΔx

-ΔMSΔt=ΔρSΔx

переходя к пределу при Δx→0, Δt→0 получаем уравнение

-уравнение неразрывности

Обычно плотность меняется незначительно поэтому ,

Запишем теперь для элемента жидкости заключенного м/у сеч. 1 и 2 второй закон Ньютона:

;

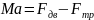
сила вязкого трения о стенки трубы которая пропорциональна скорости потока и боковой поверхности элемента жидкости

Переходя к пределу Δх→0 и обозначая через

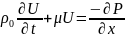уравнение движения

5. Основные определения уравнений в частных производных.

Уравнения связывающие независимые переменные х1,х2,хn фнк этих переменных U(х1,х2,хn) и ее частное производное наз. уравнением частных производных. Опред.1:порядок старшей производной входящее в уравнение наз порядком уравнения. Опред2: если уравнение линейное относительно неизвестной функции и ее частных производных то оно наз линейным уравнением частн.производных. Опред3: Частным решением уравн част производных наз всякая фнк вида U=ψ(х1,х2,хn) кот будущее подставлена в уравнение вместо неизвестной функции обращает это уравнение в тождество. (1)

Уравнение(1) исходя из определения можно наз линейным уравнением 2-го порядка. Данное уравнение классифицируется в зависимости от знака произведения: Д=-α1∙α2.

Опред4: если Д>0, то уравн(1) наз ур гиперболического типа, если Д=0, то –эллиптического типа, если Д<0 то параболич/го типа. Опред5:если f(х,t)=0 то уравнение наз однородным, в противном случае неоднородным. Пример1: Рассмотрим уравнение частных производных: (2), где U-неизвестные фнк переменных x и t. Данное уравнение 2го порядка параболического типа. Проверим, что частным решением этого уравнения является фнк: ,где А-производная постоянная. , , , ,

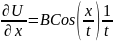, . Согласно теореме ∑ данных фнк также будет являться решением. Пример 2: Рассмотрим ур 1го порядка: (3), (4), легко проверитьчто фнк(4) удовлетворяет(3), где произвольная фнк от xпоэтому фнк(4) по аналогии с общим решением диф.ур.наз общим решением уравнения(3). Пример 3: (5), , , где -произвольная фнк. 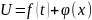- это выражение определяет общее решение уравнения(5). Т.о. делаем вывод общее решение ур частных производных содержит производные функции. В отличие от общих решений обыкновенных диф.ур., содержащих произвольное постоянное.

6. Классификация уравнений в частных производных. Однородные и неоднородные уравнения в частных производных.

Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяются спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например, пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например, u(x,t) в некоторой области определения аргументов 0<x<L и 0<t<T. Граничные условия определяются как заданные временные зависимости функции и, или производных этой функции, на границах расчетной области 0 и L, а начальные — как заданная и (х, 0).

Сами уравнения в частных производных (несколько условно) можно разделить на три основных типа:

А)параболические — содержащие первую производную по одной переменной и вторую — по другой, причем все эти производные входят в уравнение с одинаковым знаком;

Б)гиперболические— содержащие первую производную по одной переменной и вторую — по другой, входящие в уравнение с разными знаками;

В)эллиптические — содержащие только вторые производные, причем одного знака.

Некоторые более сложные уравнения нельзя однозначно подогнать под приведенную классификацию, тогда говорят о гибридных типах уравнений.

Уравнение вида , где a(x)=(a₁,а₂,…а_n), х=(х₁,х₂,…х_n)-n-мерные векторы, является линейным однородным уравнением в частных производных первого порчдка, если компоненты вектора коэффициентов a не зависит от неизвестной функции u.

Неоднородное уравнение :