35 Моделирование горизонтальных скважин и трещин грп

Для моделирования гориз-х скважин, направленых вдоль одной оси Х или Y применимы уравнения, (где z заменяется на x или y):

(1)

(2)

Допустим что скважина направлена вдоль оси Y.

Если , истинное значение r₀ должно быть выше чем в(2). Выражение для r₀ аналогично (2) где Х заменяется Z имеет погрешность до 10%.

(до кровли, подошвы)

Можно определить:

(3)

(4)

Исключение составляет составляет ГРП

Уравнение решается совместно с уравнением, определяющим распространение давление вокруг трещины.

Когда отношение прон-ти трещины к прон-ти пласта стрем-ся к , а ширина трещины пренебрежима мала по сравнению с длиной, тогда дебит и распр-е давления:

(5)

(5), f-полудлина трещины,

P-давление в т.z, z=x+iy

Трещины ГРП

Рассм. м/д моделирования трещин как совокупность трещин

(6)

Из ур-ий (6) и(5) :

Где z_i – комплексная координата i-го угла

r_i – расстояние точек перес-я трещины с границами ячеек

36. Обобщение формул притока на случай многофазной фильтрации

В случае многофазной фильтрации приток каждой фазы в скважину определяется Q=Kλ_e(P_0l-Pw) ; λ_l=(Kпl)/(μ_cB_c) ; l=H,b,г (13)

На скв. Может быть задан дебит либо одной фазы, либо жидкости, либо всех фаз. Если задан дебит нефти, то дебиты воды и газа определяются:

При Qk: Qос=k[λн(Pан-Pc)+lb(Pob-Pc)] (15)

Если задан суммарный расход:

Дебиты фаз по отдельности:

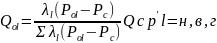
Решая совместно с уравнениями фильтрации уравнения 15, 16, 17, при заданном дебите можно вычислить неизвестное забойное давление. Подивижность фазы зависит от уравнения и насыщенности ячейки в которой расположена скважина. Если размер ячейки не велик, то соответствующее значение в ячейке и вблизи скважины различаются несущественно. Необходимо учитывать локальные эффекты которые могут быть связаны либо с конусообразованием, выделением газа ниже P<Pнас. Для того чтобы учесть эффект, основными средствами учета являются локальное измельчение сетки или введение спец. Фазовых модифицированных проницаемостей.

37 Моделирование скважин, вскрывающих несколько слоев

При моделировании скважин, вскрывающих несколько слоев, дебит фазы вычисляется по формуле:

Qi= , где l=н,в,г (1)

Рск- забойное давление ячейки к.Суммарный дебит определяется как :

Q=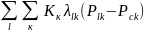 (2)

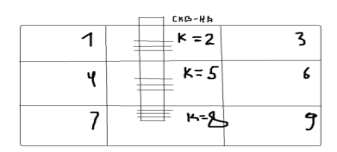Рис1.Скважина, вскрывающая несколько слоев.

Часто капиллярными силами пренебрегают, тогда р1к =рк

Если в качестве граничного условия на скважине задается забойное давление pс, обычно указывается глубина, которой оно соответствует, например, кровля пласта D0. Тогда возникает задача определения значений забойного давления pс для каждого слоя сеточной области. В простейшем случае предполагается, что забойное давление распределено по гидростатическому закону:

P_ck = , (3)

Здесь Dk - глубина соответствующей ячейки, – удельный вес фазы на этой глубине, γ — средний удельный вес смеси в стволе

скважины. Вместо гипотезы о гидростатическом распределении давления в

стволе скважины при расчете дебитов из отдельных слоев иногда предполагают постоянство депрессии р_к — p_сk = ∆р = const.

В этом случае дебит каждого слоя пропорционален K_k 𝜆_lk .

Недостатком такого подхода является неучет распределения давления в стволе скважины. Поэтому никак не могут быть смоделированы такие явления, как внутрискважинные перетоки флюидов из одного изолированного слоя

в другой.

Подстановка выражений (3) в (1) и (2) позволяет выразить дебит скважины через заданное забойное давление. Например, выражение для фазового дебита (1) примет вид:

Q_l=