Понятие о физ. И мат. Моделях
Разработка м/р УВ представляет собой комплексную проблему для успешного решения, кот. требует привлечения знаний и опыта накопленных в различных областях науки и инженерной практики. Осн. инструмент для принятия обоснованной стратегии и практического решения при разработке УВ м/р яв-ся моделир. Процессов извлечения нефти и газа. Каждое м/р уникально и как мы знаем, неправильное применение тех или иных воздействий на пласт может привести к непоправимым последствиям. Поэтому оценку эффективности различных технологий с учетом особенностей конкретного объекта и дальнейшее прогнозирование поведения данного объекта целесообразно осущ. с помощью предварительного моделирования. Физическая модель. В большинстве случаев ФМ имеет ту же физ.природу, что и изучаемый объект. Эксперим. на физ.мод.проводят для исследований закономерностей изуч.явления. Все модели строятся по подобию. Однако изготовить полностью подобную модель не возможно поэтому этот м-д не получил широкого распространения при прогнозировании м/р УВ. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ. Обычно исп. для лабор.исследований. По изуч.св-в пород и насыщающих их флюидов. Среди физ.моделей отдельную группу составляет аналоговую модель, кот.воспроизводит процесс физически подобные оригиналу, но подчин.др.группе физ.законов (ЭГДА).МАТМОД представляет собой приближ.описание поведения изуч.объекта с помощью мат.символов. Процесс матмод-изуч.объекта с помощью матмод можно условно подразделить на 4 этапа:
1.Формир.мат.терминов, законов, описыв. Поведение
2. Решение прямой задачи,т.е. получение путем исслед.модели выходных данных для дальнейшего сопоставл.с рез-ми наблюд. За объектом моделирования
3. Адаптация модели по рез-там наблюд.,решение обратных задач,т.е. определение хар-к моделей.кот.оставались неопределенными
4. Анализ моделей,ее модерниз.по мере накопления новой информ. об изуч. объекте, постепенный переход к более новой совершенной технологии.
2. Цель математического и физического моделирования пластов.
Используя модели получают множество выходных данных, для изучения характеристик пластов, механики движения флюидов в пористой среде.
I-я задача: Опред-е характера залегания нефти, оценка запасов по пласту
2 В случае многопластовых месторождений могут потребоваться данные по добыче и запасам нефти для какого либо горизонта или зоны.
при моделировании объекта, расчлен. на отдельные пласты полученная информация позволит более эффективно планировать добычу и намечать интервалы вскрытия пластов в скв.
3 Дебиты нефти и газа – основные выходные данные модели, они могут быть получены как по отдельным скважинам, по участкам, так и по всему пласту
4 одновременно с дебитами на модели можно определить и Рзаб в скв
5 в проектах вторичных методов разработки, вне зависимости от вида закачиваемого агента, воды или газа необходимо знать его объемы и давления нагнетания.
6 С помощью модели определяем наиболее подходящую ( рациональную) схему разработки
7) перемещением флюидов в пласте можно управлять, по этому положение скважин и требуемые отборы выбирают такими, чтобы была возможность для управления продвижением флюидов в нужном направлении, а так же определяют пути вытеснения нефти рабочим агентом при данном расположении нагнет скв. Анализируя перемещение флюидов, можно найти местонахождение новых эксплуатационных скважин, необход для увеличения конечной нефтеотдачи
8) по данным моделирования устан оптимальную последовательность бурения, последовательность перевода экспл скв в нагнет
N-кол-во пробуренных скв
9 в системах газохранилищ в период неполного потребления газа специалисты управляют его поступлением в подземные хранилища из отдельных месторождений. В период отопительного сезона этот газ извлекается, при этом необходимо определить скорости извлеч газа, скорости вторичного заполнения газом хранилищ, так же требуестя определить состав газа.
10) При моделировании скв получают след данные:
а) крит. дебиты для предотвращения конусообразования газа и воды
б) максимально эффективные дебиты для обеспечения оптимальной работы скв
в) степень воздействия интервалов перфор и размеров трещин на продуктивность скважины
3. Уравнения математической физики
Некоторые понятия об уравнениях в частных производных.
Многие задачи математической физики приводят к ДУ в частных производных.
Определение 1: Ур-ия связывающие независимые переменные x1,x2…xn, фнк этих переменных U(x1;x2…xn) и ее частные производные называются уравнением в частных производных.
Определение 2: Порядок старшей производной входящей в уравнение, называется порядком уравнения.
Определение 3: Если уравнение линейно относительно независимой ФНК, и ее частных производных, то оно называется линейным уравнением в частных производных.
Определение 4: Частным решением уравнения в частных производных на-ся всякая фнк вида U=φ(x1;x2..xn), которая будучи подставлена в уравнение вместо неизвестной функции обращает это уравнение в тождество
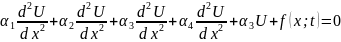(1)
Αi-(i=1..5) и f – заданные фнк xi, причем α1 и α2, одновременно не равны 0, x-пространственная координата, t – время
Уравнение (1) является линейным уравнение 2-го порядка. Данное уравнение классифицируется в зависимости от знака произведения D=-α1*α2
Определение 5: Если D>0, то уравнение (1) называется уравнением гиперболического типа. Если D=0, то параболического типа.
Определение 6: Если f(x;t)=0, то уравнение (1) называется однородным, в противном случае неоднородным.
Как и в случае обыкновенных ДУ линейная комбинация решений линейного однородного уравнения в частных производных также является решением.
U1;U2…Un – частные решения линейного однородного уравнения в частных производных, то любая фнк вида U=C1U1+C2U2+..CnUn=ΣCiUi, также является решением этого уравнения. Сi- произвольная постоянная.