затраты на управленческий персонал.

2. Переменная составляющая издержек на хранение, прямо пропорциональная объему хранимого запаса:

• потери от омертвления средств, вложенных в покупку складских запасов;

• издержки по страхованию запасов;

• потери от порчи хранимых запасов;

• прямые затраты на производственный персонал.

Графическое представление суммарных издержек за период времени (Т) (годовые издержки) в зависимости от размера пар­тий поставки (Q) характеризует график, изображенный на рис. 1:

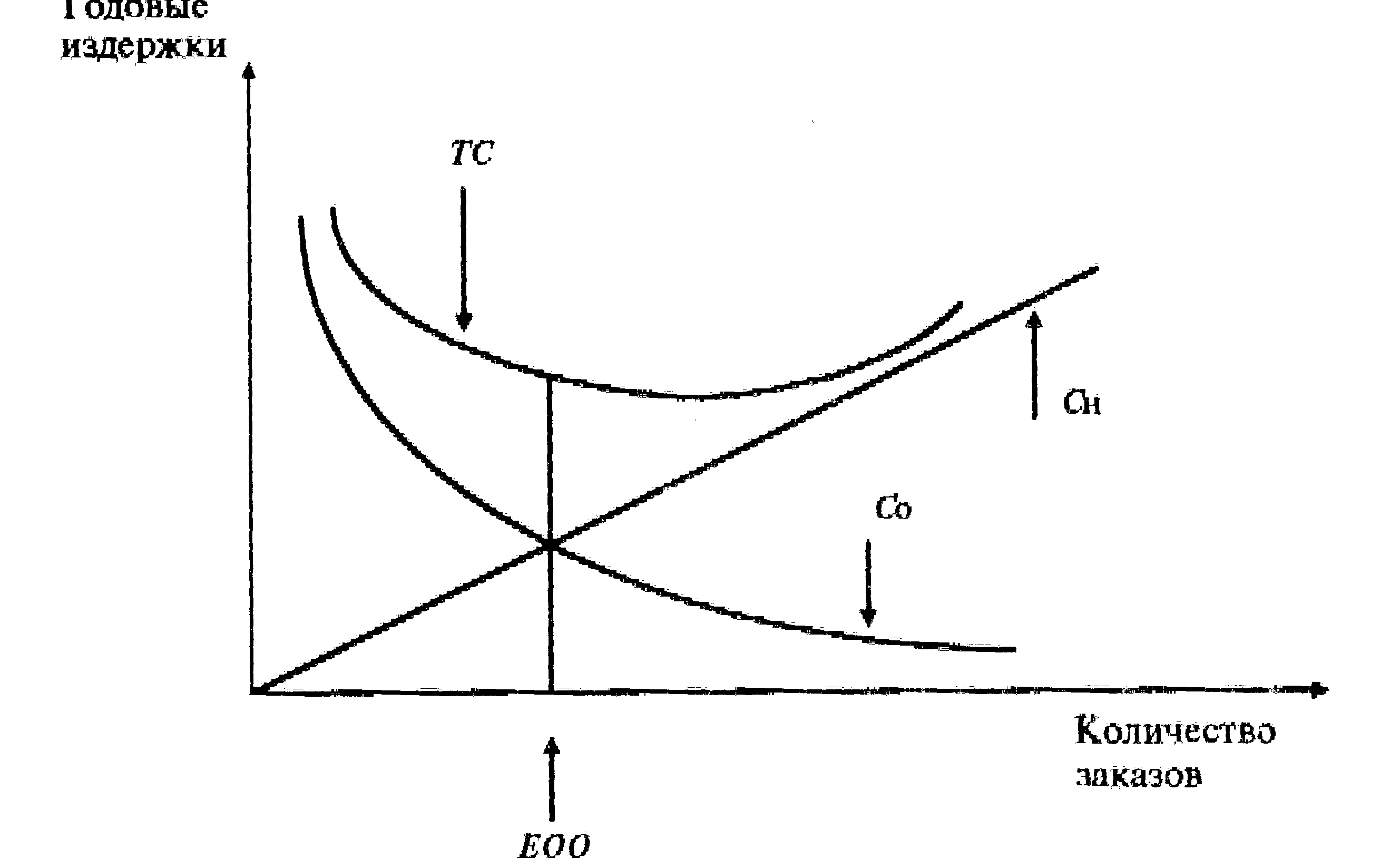
Рис. 1. Графическое представление суммарных издержек.

На графике ТС = С_о + С_н

Кривая общих годовые издержек является достаточно по­логой вблизи точки минимума. Это свидетельствует, что вблизи точки минимума размер запаса может колебаться в некоторых пределах без существенного изменения общих издержек.

3. Модели управления запасами

В целом теория управления запасами развита достаточно хорошо. Разработаны многочисленные модели оптимизации величины заказа. Рассмотрим несколько простейших детерминированных моделей управления запасами.

Основная модель управления запасами.

Предпосылки: 1) темп спроса на товар известен и постоянен; 2) получени6е заказа мгновенно; 3) отсутствуют количественные скидки при закупке больших партий товара; 4) исключается дефицит в случае своевременного заказа. Определить оптимальный размер заказа, срок выполнения заказа, их количество за период и точку восстановления (т.е. уровень запасов, при котором необходимо делать новый заказ) таким образом, чтобы затраты за весь период планирования были минимальны.

Объем п оставок

текущий

произв.

запас

страховой Т

запас

период между

1-й и 2-й поставками

Примем следующие обозначения:

р – цена товара;

Q – размер одной партии заказа;

Т – протяженность периода планирования;

d – интенсивность спроса в единицу времени (D – за весь период планирования);

h – издержки хранения единицы товара в единицу времени (H – за весь период);

s – организационные издержки на одну партию товара.

Совокупные издержки заказа за весь период S = (D/Q) ∙ s;

Совокупные издержки хранения – (Q/2) ∙ H;

Общая стоимость товара за весь период – p ∙ D;

Общие издержки за весь период планирования

Для нахождения размера оптимального заказа Q* (точка минимума для функции С(Q)) найдем первую производную функции С и приравняем ее к нулю:

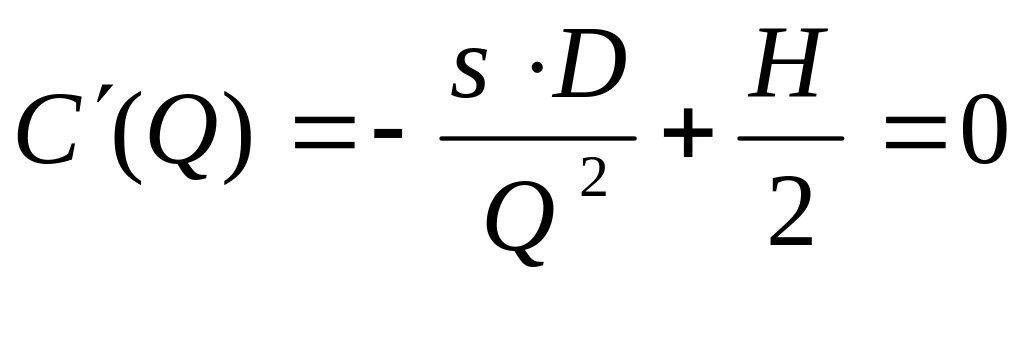
Отсюда оптимальный размер заказа:

Полученная формула называется формулой Уилсона (Харриса) или формулой оптимального размера заказа.

Оптимальное число заказов за период: N = D/Q*.

Оптимальное время между заказами (или продолжительность цикла между заказами): t* = Q*/d или t* = T/N.

Пример 1. Годовой спрос оценивается в 500 ед. товара. Средние издержки заказа – 10000 руб. Годовые издержки хранения – 20000 руб. Цена товара – 50000 руб. Определить оптимальный размер партии товара, количество заказанных партий и совокупные годовые издержки при условии, что заказ выполняется мгновенно и магазин работает без выходных.

Исходные данные: D = 500; s = 10000; p = 50000; H = 20000.

Оптимальный размер заказа:

Общие затраты:

=250000 +223214+224000=697214.

Оптимальное количество заказанных партий: N = D/Q* = 500/22,4 = 22,3.

При этом число дней между заказами: t* = T/N = 365/22,3 = 16,4 дн.

Модель оптимального размера заказа при получении заказа с течением времени. В основной модели предполагалось, что заказ на новую партию товара выполняется мгновенно. Новая партия товара поступает в течение одного дня или ночи. Но чаще встречаются ситуации, когда для выполнения заказа необходимо какое-то время. В этом случае заказ необходимо делать заранее, имея на складе запас товара, необходимый для удовлетворения спроса за время выполнения заказа. Уровень запасов, при котором необходимо делать новый заказ, называется точкой восстановления. Он рассчитывается по следующей формуле:

R = d ∙ G ,

где R – точка восстановления запасов (точка заказа);

d – интенсивность спроса в единицу времени;

G – время выполнения заказа.

Пример 2. Рассмотрим исходные данные примера 1, но при условии, что время выполнения заказа 5 дней, а количество рабочих дней в году равно 250. Годовой спрос оценивается в 500 ед. товара. Средние издержки заказа – 10000 руб. Годовые издержки хранения – 20000 руб. Цена товара – 50000 руб.

Оптимальный размер партии товара, количество заказанных партий и совокупные годовые издержки рассчитываются также, как и в первом примере.

Спрос на товар в единицу времени d = годовой спрос, деленный на количество рабочих дней в году = 500/250 = 2.

Точка восстановления (точка заказа):

R = спрос в единицу времени, умноженный на время выполнения заказа = 2∙5 = 10.

Модель оптимального размера заказа, при условии, что допускается дефицит товара (модель ускоренного использования запасов). В ряде случаев, если интенсивность потребления материальных ресурсов такова, что может возникнуть определенный дефицит материалов, в модели управления запасами допускается дефицит товара и, соответственно, связанная с дефицитом упущенная прибыль. Если этот дефицит сопоставим с затратами на содержание запасов, например, если издержки хранения достаточно велики, или складские помещения не допускают хранения большой партии товара, или товар скоропортящийся. В этом случае оптимальный размер заказа рассчитывается по формуле:

где Р – упущенная прибыль за весь период планирования, связанная с дефицитом единицы товара.

t₁ - время, в течение которого запас на складе в наличии.

q_опт t₂ - время, которое запас отсутствует.

q_н - начальный размер запаса (как правило, мень-

q_н ше величины оптимальной партии)

дефицит

t₁ t₂

Модель производственных поставок (модель затянувшейся поставки). В промышленном производстве очень часто производство товаров для пополнения запасов идет одновременно с удовлетворением спроса на товар.

q Период времени разделяется на 2 части.

q_max в период t₁: поступление мат. ресурсов и их расход (u>d,

(u-d)t u-dt u-поступление, пр-во)

t₁ t₂

В этом случае к исходным данным основной модели добавляются следующие параметры: u – производительность линии (единиц товара в год), s – издержки производства.

Тогда скорость пополнения запасов будет равна u – d. За время выполнения заказа при интенсивности производства u произведено Q единиц товара. Тогда u ∙ t = Q, или t = Q/u. Максимальный уровень запаса, достигнутый к концу этого времени :

Средний уровень запасов равен половине максимального:

Совокупные издержки хранения:

Совокупные издержки заказа: .

Таким образом, общие издержки вычисляются по формуле:

Оптимальный размер поставок получаем, приравнивая к нулю производную:

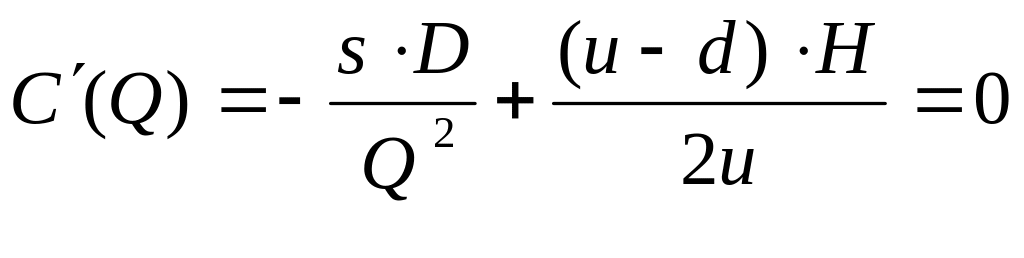
Отсюда оптимальный размер заказа:

Следовательно, максимальный уровень запасов:

Модель поставок с количественными скидками. Многие компании часто предлагают оптовым покупателям количественные скидки за крупные партии товара. Другими словами, если размер партии товара Q меньше определенной величины Q₁, то товар продается по цене р₁. При размере партии Q ≥ Q₁, товар продается по цене р₂ (р₂ > р₁) и т.д.

В этом случае общие издержки определяются следующим образом:

Функция достигает минимума в точке Q*:

Если Q*≥ Q₁, следовательно, Q* – оптимальный размер партии товара, если Q*< Q₁, то сравниваем С(Q*) и С(Q₁). Если С(Q₁) окажется меньше С(Q*) то оптимальным размером партии товара будет Q₁.

Пример 3. Рассмотрим исходные данные примера 1, при условии, что при размере партии товара не менее 30 ед., цена снижается до 40000. Годовой спрос оценивается в 500 ед. товара. Средние издержки заказа – 10000 руб. Годовые издержки хранения – 20000 руб. Исходная цена товара – 50000 руб. Определить оптимальный размер партии товара, количество заказанных партий и совокупные годовые издержки при условии, что заказ выполняется мгновенно и магазин работает без выходных.

Оптимальный размер заказа, как уже рассматривалось в примере 1, равен:

Так как Q<30, то:

=250000 +223214+224000=697214.

=200000 +166666,7+300000=666666,7.

Следовательно, оптимальный размер партии составляет 30 ед. товара.

Оптимальное количество заказанных партий товара N = D/Q* = 500/30 = 16,7.

При этом число дней между заказами t* = T/N = 365/16,7 = 21,9 дн.