Федеральное агентство по образованию Всероссийский заочный финансово-экономический институт

КОНТРОЛЬНАЯ РАБОТА № 1

по дисциплине «Эконометрика»

Вариант № 3

Исполнитель:

студентка III курса (вечер)

факультет: финансово-кредитный

специальность: финансы и кредит

№ зачетной книжки:

Руководитель: Швецова С.Т.

Калуга 2006

Задача 1

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (у, млн. руб.) от объема капиталовложений (х, млн. руб.).

№ п/п	Объем выпуска продукции, млн. руб., у	Объема капиталовложений, млн. руб., х
1	69	38
2	52	28
3	46	27
4	63	37
5	73	46
6	48	27
7	67	41
8	62	39
9	47	28
10	67	44

Требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 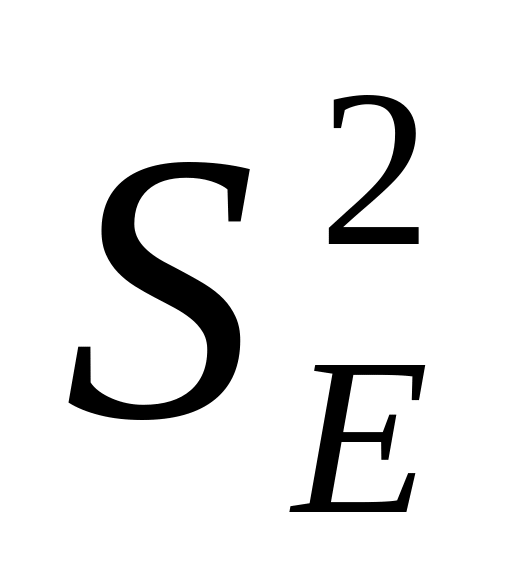; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента ( = 0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера ( = 0,05), найти среднюю относительную ошибку аппроксимации. Сделать выводы о качестве модели.

6. Осуществить прогнозирование среднего значения показателя у при уровне значимости = 0,1, если прогнозное значение фактора х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения у, точки прогноза.

8. Составить уравнения нелинейной регрессии:

   • гиперболическая

   • степенной

   • показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Решение

1. Построим линейную модель регрессии.

Уравнение линейной регрессии имеет вид:

Построение линейной регрессии сводится к оценке ее параметров – и .

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров и , при которых сумма квадратов отклонений фактических значений результативного признака от теоретических минимальна:

.

Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров и и приравнять их к нулю. Обозначим через , тогда:

.

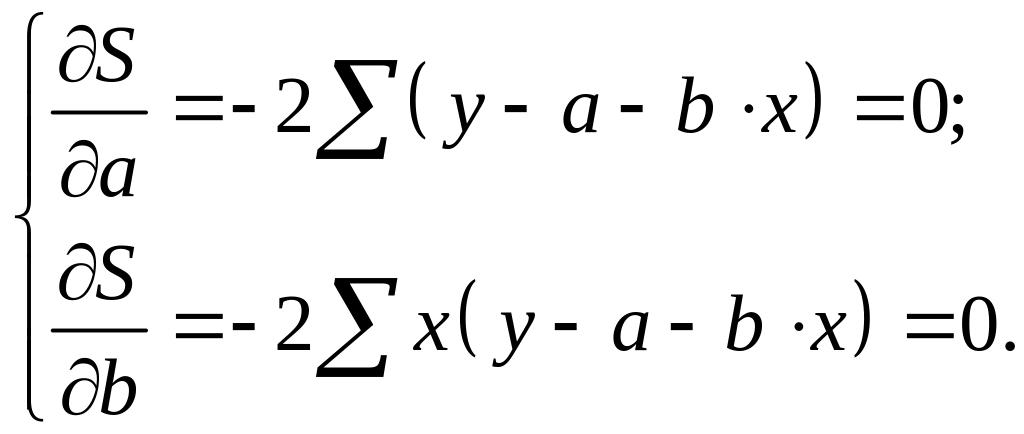
После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров и :

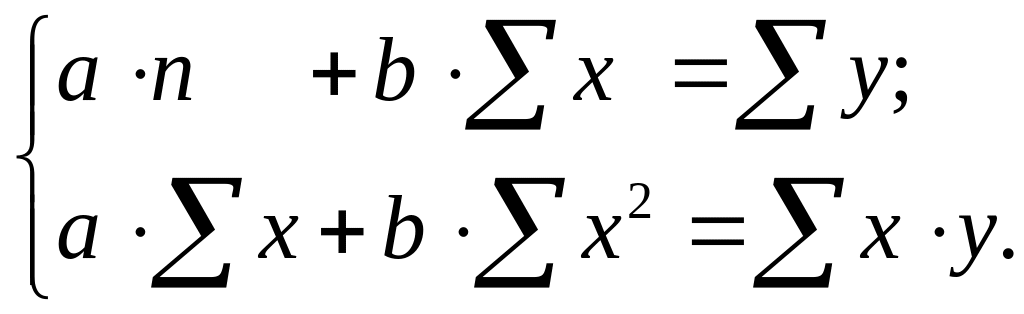
Решая систему уравнений, найдем искомые оценки параметров и . Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы:

, ,

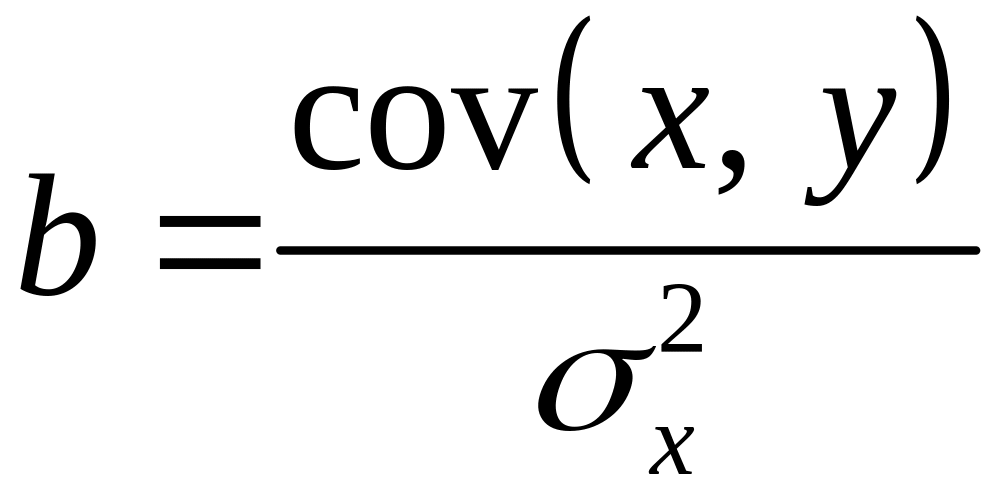где – ковариация признаков и ,

– дисперсия признака и

, , ,

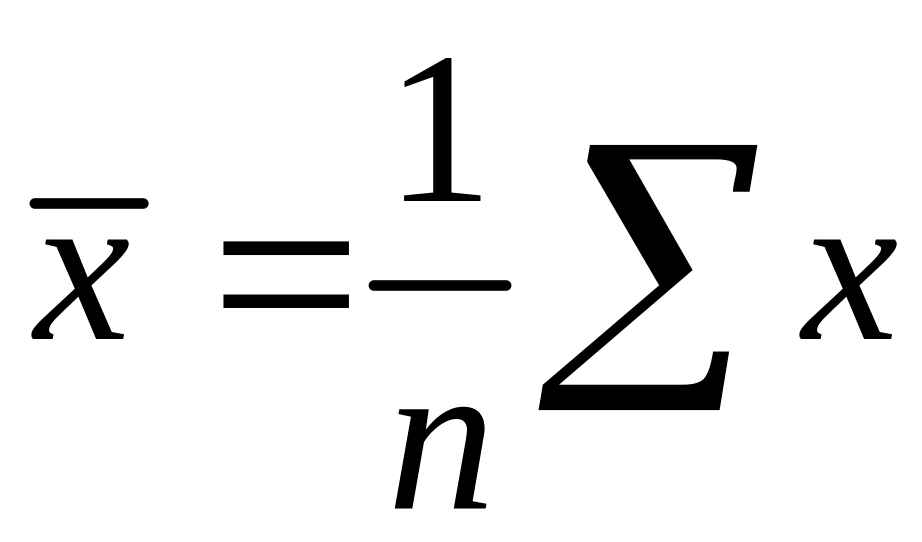Для удобства дальнейших вычислений составим таблицу 1.1 ( = у – ŷ).

Рассчитаем параметры линейного уравнения парной регрессии . Для этого воспользуемся формулами:

;

.

Получили уравнение: .

Т.е. b показывает, что при увеличении объема капиталовложений на 1 млн. руб., объем выпуска продукции в среднем увеличивается на 1,3191 млн. руб.

а = 12,5733, означает, что относительное изменение результата происходит медленнее, чем изменение фактора.

Таблица 1.1

№	у	х	yx		( )2		( )2	x2	ŷ		2
1	69	38	2622	2,5000	6,2500	9,6000	92,1600	1444	62,6977	6,3023	39,7195	0,0913
2	52	28	1456	-7,5000	56,2500	-7,4000	54,7600	784	49,5070	2,4930	6,2149	0,0479
3	46	27	1242	-8,5000	72,2500	-13,4000	179,5600	729	48,1880	-2,1880	4,7872	0,0476
4	63	37	2331	1,5000	2,2500	3,6000	12,9600	1369	61,3786	1,6214	2,6290	0,0257
5	73	46	3358	10,5000	110,2500	13,6000	184,9600	2116	73,2502	-0,2502	0,0626	0,0034
6	48	27	1296	-8,5000	72,2500	-11,4000	129,9600	729	48,1880	-0,1880	0,0353	0,0039
7	67	41	2747	5,5000	30,2500	7,6000	57,7600	1681	66,6548	0,3452	0,1191	0,0052
8	62	39	2418	3,5000	12,2500	2,6000	6,7600	1521	64,0167	-2,0167	4,0672	0,0325
9	47	28	1316	-7,5000	56,2500	-12,4000	153,7600	784	49,5070	-2,5070	6,2852	0,0533
10	67	44	2948	8,5000	72,2500	7,6000	57,7600	1936	70,6120	-3,6120	13,0468	0,0539
Сумма	594	355	21734		490,5000		930,4000	13093			76,9668	0,3649
Ср. знач.	59,4000	35,5000	2173,4000					1309,3000
Квадрат	3528,3600	1260,2500