
Вариант 1 Задача 1
При испытаниях генератора трехфазного тока многократно измеряли напряжение между двумя обмотками (признак X). Результаты измерений (в вольтах) записаны в виде статистического ряда.
3,3 |
3,5 |
4,4 |
4,1 |
4,3 |
3,6 |
3,7 |
4,9 |
3,9 |
3,6 |
4,9 |
3,7 |
3,4 |
4 |
4,2 |
3,7 |
3,1 |
3,1 |
5 |
4,6 |
3,1 |
4,9 |
3 |
3,3 |
3,5 |
3,8 |
4,5 |
4,3 |
3,5 |
4,1 |
4,2 |
3,4 |
3,4 |
3,6 |
3,3 |
3,7 |
4,1 |
4,5 |
3,8 |
4,8 |
3,7 |
4,4 |
4,2 |
4,6 |
3,9 |
3,1 |
4,4 |
3,7 |
4,5 |
3,5 |
Произвести статистическую обработку результатов измерений:
1) построить интервальный вариационный ряд;
2) построить гистограмму относительных частот, эмпирическую функцию распределения и ее график (кумулянту);
3) найти выборочные
числовые характеристики
 ;
;
4) по геометрическим характеристикам и по соотношениям между числовыми характеристиками выдвинуть гипотезу о законе распределения признака X;
5) проверить
гипотезу о законе распределения признака
X
по критерию
 -квадрат
при уровне значимости 0,05;
-квадрат
при уровне значимости 0,05;
6) найти 95%-ые доверительные интервалы для математического ожидания и среднего квадратического отклонения.
Задача 2
Экспериментальная зависимость признака Y от фактора X имеет вид:
Xi |
2,0 |
2,2 |
2,3 |
2,5 |
2,6 |
2,8 |
3,0 |
3,1 |
Yi |
1,016 |
1,022 |
1,027 |
1,035 |
1,036 |
1,040 |
1,049 |
1,052 |
Требуется:
1) найти уравнение
линейной регрессии
 ;
;
2) найти выборочный
коэффициент корреляции
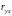 ;
;
3) выяснить
значимость уравнения регрессии при
 ;
;
4) построить
линию регрессии и экспериментальные
точки
 .
.
Вариант 2 Задача 1
Были проведены измерения диаметров (признак X) 50 шестерен редуктора после обработки на токарном станке. Результаты измерений (в мм) записаны в виде статистического ряда.
7,2 |
16,6 |
19 |
11,6 |
12 |
10,9 |
18,3 |
18,5 |
7,7 |
13,2 |
7,8 |
17,1 |
11,9 |
14,7 |
14,3 |
9,7 |
2 |
11,2 |
12,9 |
9,3 |
10,6 |
18,2 |
8,8 |
4,4 |
13 |
13,9 |
6,7 |
14,3 |
7,8 |
18 |
8,3 |
5,3 |
3,3 |
4 |
4,3 |
11,9 |
14,7 |
6,7 |
12,3 |
13,9 |
5,6 |
16,3 |
10,9 |
18,7 |
11 |
11 |
12,4 |
7,4 |
9 |
6,2 |
Произвести статистическую обработку результатов измерений:
1) построить интервальный вариационный ряд;
2) построить гистограмму относительных частот, эмпирическую функцию распределения и ее график (кумулянту);
3) найти выборочные числовые характеристики ;
4) по геометрическим характеристикам и по соотношениям между числовыми характеристиками выдвинуть гипотезу о законе распределения признака X;
5) проверить гипотезу о законе распределения признака X по критерию -квадрат при уровне значимости 0,05;
6) найти 95%-ые доверительные интервалы для математического ожидания и среднего квадратического отклонения.
