5 Сигналы
В зависимости от определенности во времени различают сигналы:
непрерывный (аналоговый);
дискретный.
Непрерывный (аналоговый) сигнал – сигнал, который определен в любой момент времени.
Дискретный сигнал – сигнал, который определен лишь в некоторые моменты времени.
При исследовании АСУ и их элементов используют ряд стандартных сигналов, называемых типовыми воздействиями. Эти воздействия описываются простыми математическими функциями и легко воспроизводятся при исследовании АСУ. Использование типовых воздействий позволяет унифицировать анализ различных систем и облегчает сравнение их передаточных свойств. Наибольшее применение находят следующие типовые воздействия:
ступенчатое;
импульсное;
гармоническое;
линейное.
Под сигналом (в общем смысле этого слова) в дальнейшем будем понимать физический процесс, с заданной точностью отображающий сведения о состоянии изучаемого процесса или объекта и пригодный для его дальнейшей обработки и передачи на расстояние.
Математическое представление сигналов
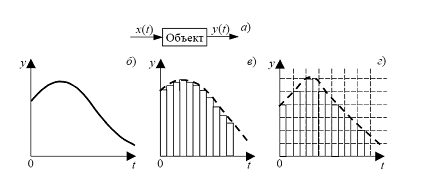
Рис. 7 а – блок-схема системы; б – непрерывное; в – дискретно-непрерывное; г – дискретное представление сигналов
Единичный скачок (Unit step ) - Тестовый сигнал, в котором амплитуда подвергается резкому ступенчатому изменению от одной постоянной величины до другой постоянной величины в момент времени t0. Это функция Хевисайда.
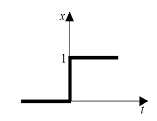
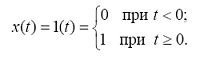
Рис. 8 Единичный скачок 1(t)
Функция равна 0, когда аргумент отрицательный и равна 1, когда аргумент положительный.
Дельта-функция (функция Дирака)
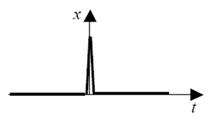
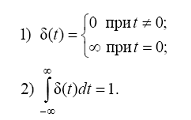
Рис. 9 Единичная импульсная функция – дельта-функция
Эту физически нереализуемую функцию можно представить как импульс бесконечно малой длительности и бесконечно большой амплитуды, т.е. как предел, к которому стремится прямоугольный импульс с основанием Δt и площадью, равной единице, если Δt → 0 так, чтобы площадь импульса сохранялась равной единице.
Синусоидальный (гармонический) сигнал
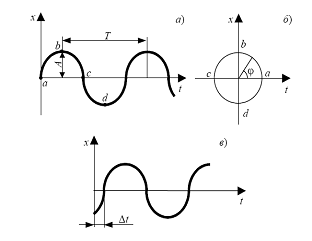
Рис. 10 Гармонический сигнал
Гармонический сигнал характеризуется параметрами: амплитуда – А; период – Т; фаза – ϕ.
Пример 1. Если на исследуемом объекте резко открыть вентиль, в результате чего расход подаваемого вещества изменится скачком с F1 до F2, то говорят, что на входе объекта реализован скачкообразный сигнал величиной F2 – F1 , и если эта разность равна единице, то на входе реализуется единичный скачок.
Изменение в установке вентиля расход пара не мгновенно будет изменять выходную величину температуры. Теплоёмкость воды будет заставлять температуру медленно перемещаться в новое положение.
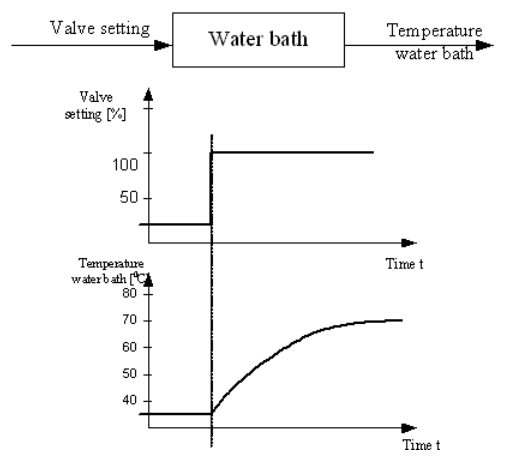
Рис. 11 Характеристики управляемой системы «водяная баня»
Пример 2. При управлении расходом динамический ответ быстрый. Изменение в положении вентиля вызовет немедленное изменение расхода, так что изменение в объёмном расходе почти немедленно повторяет изменение во входном положении вентиля.
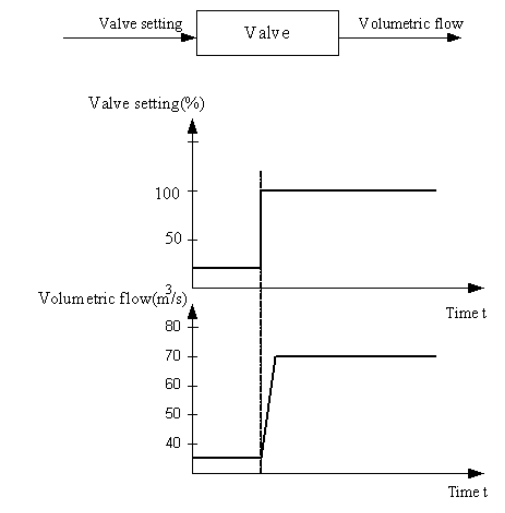
Рис. 12 Характеристики управляемой системы «вентиль»
Ответ системы на изменение состояния определяется временной константой. Управляемые системы (технические системы) могут показывать существенно разные временные константы):
температура: очень медленный
поток (расход): медленный
скорость вращения (rotary): относительно быстрый
освещённость: очень быстрый
Из примеров видно, что ответы разные.