2) Интегрирующее

2.1) Идеальное интегрирующее

Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины:

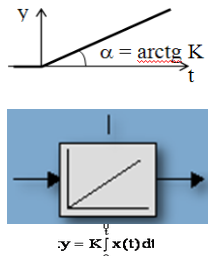
Рис. 13  Выходной сигнал идеального интегрирующего звена и его обозначение 

При подаче на вход звена ступенчатого воздействия x (t) = 1 выходной сигнал постоянно возрастает (Рис. 13): h(t) = K^.t.

Это звено астатическое, т.е. не имеет установившегося режима.

 Примером такого звена может служить емкость, наполняемая жидкостью (Рис. 14). Входной параметр – расход поступающей жидкости, выходной - уровень. Изначально емкость пуста и при отсутствии расхода уровень равен нулю, но если включить подачу жидкости, уровень начинает равномерно увеличиваться.

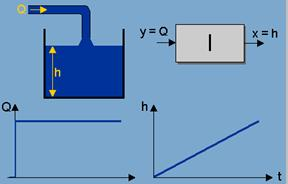
Рис. 14 Ёмкость, наполняемая жидкостью (без слива)

2.2) Реальное интегрирующее.

Передаточная функция этого звена имеет вид

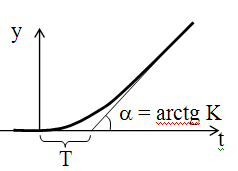
 Рис. 15 Передаточная функция реального интегрирующего звена

Переходная характеристика в отличие от идеального звена является кривой (Рис. 15)  h(t) = K^.(t – T) + K^.T^.e ^-t/T.

Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора. Если напряжение на двигатель не подается, то ротор не двигается и угол его поворота можно принять равным нулю. При подаче напряжения ротор начинает раскручиваться, а угол его поворота сначала медленно вследствие инерции, а затем быстрее увеличиваться до достижения определенной скорости вращения.

3) Дифференцирующее.

3.1) Идеальное дифференцирующее

Выходная величина пропорциональна производной по времени от входной:

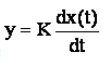   W(s) = K*s

При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию):          h(t) = K^.d(t).

3.2) Реальное дифференцирующее

Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям,   передаточные функции которых имеют вид:

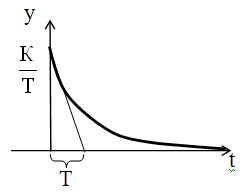
Рис. 16 Передаточная функция дифференцирующего звена

Переходная характеристика:

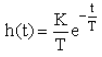
Пример звена: Электрогенератор. Входной параметр – угол поворота ротора, выходной – напряжение. Если ротор повернуть на некоторый угол, то на клеммах появится напряжение, но если ротор далее не вращать, напряжение снизится до нуля. Резко упасть оно не может вследствие наличия индуктивности у обмотки.

4) Апериодическое (инерционное)

Этому звену соответствуют дифференциальное уравнение и передаточная функция вида

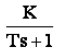
Постоянная Т называется постоянной времени.

Рис. 17 Передаточная функция апериодического (инерционного) звена

Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону (рис. 17).

5) Запаздывающее

 Если при подаче на вход объекта некоторого сигнала он реагирует на этот сигнал не моментально, а спустя некоторое время, то говорят, что объект обладает запаздыванием.

Запаздывание – это интервал времени от момента изменения входного сигнала до начала изменения выходного.

Запаздывающее звено – это звено, у которого выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t:

y(t) = x(t - t).

Передаточная функция звена: W(s) = e^-ts.

 Примеры запаздываний: движение жидкости по трубопроводу  (сколько жидкости было закачано в начале трубопровода, столько ее выйдет в конце, но через некоторое время, пока жидкость движется по трубе), движение груза по конвейеру (запаздывание определяется длиной конвейера и скоростью движения ленты) и т.д.