22 Преимущество и недостатки конических прямозубых передач

Преимущества косозубых колес: Причем, если в прямозубых колесах зубья входят в зацепление мгновенно по всей длине, то в косозубых колесах - постепенно. Благодаря этому при одинаковых неточностях в зацеплении 1) косозубые передачи работают более плавно, чем прямозубые. Кроме того 2) косозубые колеса по сравнению с прямозубыми обладают большой нагрузочной способностью как по контактным напряжениям, так и по напряжениям изгиба (Рис. 64). Недостатки: Но наряду с указанными достоинствами косозубые колеса имеют серьезный недостаток. В результате винтового расположения зубьев возникает осевая сила : , , где - угол наклона зуба к оси вращения на делительном цилиндре. Величина осевой силы так же как и плавность работы и нагрузочная способность передач зависит от угла наклона зубьев . С увеличением угла наклона повышается плавность работы и нагрузочная способность передачи, но увеличивается осевая сила приходится предусматривать сложные конструкции опорных узлов, которые бы воспринимали эти силы. При это конструкция передач усложняется. ГОСТом предусматривается для косозубых колес угол наклона их зубьев =8…15 при таких значениях угла обеспечивается с одной стороны достаточная нагрузочная способность передачи, с другой стороны небольшая осевая сила , для восприятия которой не требуется предусматривать сложные опоры.

23Преимущество и недостатки цилиндрических косозубых передач

Достоинства зубчатых передач: • Возможность применения в широком диапазоне скоростей, мощностей и передаточных отношений. • Высокая нагрузочная способность и малые габариты. • Большая долговечность и надёжность работы. • Постоянство передаточного отношения. • Высокий КПД (87-98%). • Простота обслуживания. Недостатки зубчатых передач: • Большая жёсткость не позволяющая компенсировать динамические нагрузки. • Высокие требования к точности изготовления и монтажа. • Шум при больших скоростях.

В отличие от прямозубых колес, у которых зубья располагаются параллельно оси вращения, в косозубых колесах зубья располагаются по винтовым линиям.

24 Преимущества и недостатки конических зубчатых передач.

Преимущества:

• обеспечение возможности передачи и преобразования вращательного движения между звеньями с пересекающимися осями вращения;

• возможность передачи движения между звеньями с переменным межосевым углом при широком диапазоне его изменения;

• расширение компоновочных возможностей при разработке сложных зубчатых и комбинированных механизмов.

Недостатки:

• более сложная технология изготовления и сборки конических зубчатых колес;

• большие осевые и изгибные нагрузки на валы, особенно в связи с консольным расположением зубчатых колес.

25. преимущество и недостатки передач с зацеплением Новикова

Зацепление Новикова, круговинтовое зацепление, передача Новикова — механическая передача, альтернативный эвольвентному тип зацепления, предложенный советским инженером М. Л. Новиковым в 1954[1] году для зубчатых передач.

Зубья колёс в торцевом сечении очерчены окружностями близких радиусов. Площадка контакта зубьев перемещается не по профилю зуба, как в прямозубом эвольвентном зацеплении, а вдоль него. Угол давления и скорость перемещения не изменяется.

Различают два вида зацеплений Новикова:

с одной линией зацепления (ОЛЗ) заполюсные или дополюсные.

с двумя линиями зацепления (ДЛЗ) дозаполюсные.

Преимущества

Более высокая нагрузочная способность по контактным напряжениям и напряжениям изгиба(в 1,5…1,7 раз).

Меньший уровень шума. В статье «Зацепление Новикова: Реальные возможности». указан больший уровень шума.

Более высокие передаточные числа.

Передача менее чувствительна к перекосам зубчатых колёс вследствие точечного контакта зубьев.

Недостатки

Зацепление Новикова очень чувствительно к изменению межосевого расстояния, следовательно требует более высокой точности установки колёс, более высокой жёсткости валов и их опоры;

В передачах с ОЛЗ требуется разный инструмент для нарезания зубьев колеса и шестерни, так как они имеют разный профиль;

26. преимущество и недостатки волновых зубчатых передач

Волнова́я передача — механическая передача, передающая движение за счет циклического возбуждения волн деформации в гибком элементе. Передача движения может производиться посредством зубьев, винтового принципа, а также фрикционного контакта. Изобретена в 1959 году американским инженером У. Массером.

Принцип действия

Состоит из жесткого неподвижного элемента — зубчатого колеса с внутренними зубьями, неподвижного относительно корпуса передачи; гибкого элемента — тонкостенного упругого зубчатого колеса с наружными зубьями, соединенного с выходным валом; генератора волн — кулачка, эксцентрика или другого механизма, растягивающего гибкий элемент до образования в двух (или более) точках пар зацепления с неподвижным элементом. Число зубьев гибкого колеса несколько меньше числа зубьев неподвижного элемента. Число волн деформации равно числу выступов на генераторе. В вершинах волн зубья гибкого колеса полностью входят в зацепление с зубьями жёсткого, а во впадинах волн — полностью выходят из зацепления. Линейная скорость волн деформации соответствует скорости вершин выступов на генераторе, то есть в гибком элементе существуют бегущие волны с известной линейной скоростью. Разница чисел зубьев жёсткого и гибкого колёс обычно равна (реже кратна) числу волн деформации.

Принцип работы волновой зубчатой передачи

Например, при числе зубьев гибкого колеса 200, неподвижного элемента — 202 и двухволновой передаче (два выступа на генераторе волн) при вращении генератора по часовой стрелке первый зуб гибкого колеса будет входить в первую впадину жёсткого, второй — во вторую и т.д. до двухсотого зуба и двухсотой впадины. На следующем обороте первый зуб гибкого колеса войдёт в двести первую впадину, второй — в двести вторую, а третий — в первую впадину жёсткого колеса. Таким образом, за один полный оборот генератора волн гибкое колесо сместится относительно жёсткого на 2 зуба.

Преимущества

большое передаточное отношение, при малом количестве деталей (i = 80..320)

улучшенные массо - габаритные характеристики по сравнению с обычными зубчатыми передачами

высокая кинематическая точность и плавность хода

высокая нагрузочная способность

передача момента через герметичные стенки

Недостатки

высокая напряженность основных элементов гибкого колеса и генератора волн

пониженная крутильная жесткость.

27. преимущество и недостатки планетарных зубчатых передач

Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Планетарную передачу применяют как редуктор с постоянным передаточным числом, как коробку скоростей, передаточное число в которой изменяется путём поочерёдного торможения различных звеньев (водила или одного из колёс), как дифференциальный механизм. Их успешно применяют в транспортном машиностроении, станкостроении, приборостроении и т.д. Имеется большое количество различных типов планетарных передач, но одноступенчатая планетарная передача (рис. 1) получила самое широкое распространение. Она с успехом применяется как для больших, так и малых мощностей в силовых и кинематических приводах, т.е. не имеет ограничений по применению. КПД передачи 0,96…0,98 . В передачах применяют не только цилиндрические, но и конические колёса. Зубья могут быть прямые и косые. Обычно число сателлитов С=3…6, но встречаются передачи с С>6. Наибольшее распространение получили прямозубые передачи с числом сателлитов С=3.

Достоинства планетарных передач

1) Большое передаточное число в одной ступени;

2) Малые габариты и масса. Это объясняется следующим: мощность передается по нескольким потокам, число которых равно числу сателлитов;

3) Повышенная нагрузочная способность, так как широко применяются зубчатые колёса с внутренним зацеплением (большой радиус кривизны);

4) Малая нагрузка на опоры, так как сателлиты расположены симметрично, и поэтому силы в передаче взаимно уравновешивают друг друга;

5) Планетарные передачи работают с меньшим шумом, что связанно с повышенной плавностью внутреннего зацепления и меньшими размерами колёс.

Недостатки планетарных передач

1) Повышенные требования к точности изготовления и монтажа;

2) Резкое снижение КПД передачи с увеличением передаточного числа (увеличение количества трущихся поверхностей).

29 По виду тел качения

Шариковые

Роликовые (игольчатые, если ролики тонкие и длинные);

По типу воспринимаемой нагрузки

Радиальные (нагрузка вдоль оси вала не допускается).

Радиально-упорные, упорно-радиальные. Воспринимают нагрузки как вдоль, так и поперек оси вала. Часто нагрузка вдоль оси только одного направления.

Упорные (нагрузка поперек оси вала не допускается).

Линейные. Обеспечивают подвижность вдоль оси, вращениевокруг оси не нормируется или невозможно. Встречаются рельсовые, телескопические или вальные линейные подшипники.

Шариковые винтовые передачи. Обеспечивают сопряжение винт-гайка через тела качения.

По числу рядов тел качения

Однорядные,

Двухрядные,

Многорядные;

По способности компенсировать несоосность вала и втулки[4]

Самоустанавливающиеся.

Несамоустанавливающиеся.

Область применения Опорные роликитранспортеров, ходовых колесмостовых кранов Линейные и формовочные машины Кузнечно-прессовое оборудование Прокатные станы Грузоподъемные машины и т.д

31вопрос

Подшипники качения

Подшипники качения в основном состоят из трёх частей:

- два кольца (внешнее и внутреннее);

- тела качения (могут быть различной формы: шарики или ролики);

- сепаратор, удерживающий тела качения на расстоянии друг от друга (некоторые подшипники могут не иметь сепаратора).

Наружная поверхность внутреннего кольца и внутренняя поверхность внешнего, как правило, имеют желоб, по которому и катятся, при работе подшипника, тела качения. В случае с упорными подшипниками, желоба или направляющие дорожки выполняются на торцевых поверхностях колец.

Некоторые подшипники не имеют сепаратора, который бы удерживал тела качения на определённом расстоянии друг от друга. Количество тел качения в таких подшипниках значительно больше. Это увеличивает их грузоподъёмность, но в тоже время, предельная частота вращения бессепараторных подшипников становится ниже, так как с увеличением числа тел качения, повышается и сопротивление вращению.

При работе на подшипник качения воздействуют силы, подвергающие его определённым нагрузкам. Условно эти силы можно разделить на 2 типа:

- радиальная, действующая в перпендикулярном направлении, по отношению к оси подшипника;

- осевая, действующая в параллельном направлении, по отношению к оси подшипника.

 

Условное обозначение подшипников качения в РФ (размеры подшипников)

Маркировка подшипников качения регламентируется стандартами прописанными в ГОСТ 3189-89, а также условным обозначением завода-изготовителя.

Условное обозначение подшипников качения составляют:

- основное условное обозначение, включающее в себя семь цифр;

- дополнительное условное обозначение, часть которого располагается слева от основного условного обозначения, а часть справа от него.

Чтение знаков как основного условного, так и дополнительного условного обозначения всегда производится справа налево.

Классификация подшипников качения осуществляется на основе следующих признаков:

По виду тел качения

Шариковые,

Роликовые (игольчатые, если ролики тонкие и длинные);

По типу воспринимаемой нагрузки

Радиальные (нагрузка вдоль оси вала не допускается).

Радиально-упорные, упорно-радиальные. Воспринимают нагрузки как вдоль, так и поперек оси вала. Часто нагрузка вдоль оси только одного направления.

Упорные (нагрузка поперек оси вала не допускается).

Линейные. Обеспечивают подвижность вдоль оси, вращение вокруг оси не нормируется или невозможно. Встречаются рельсовые, телескопические или вальные линейные подшипники.

Шариковые винтовые передачи. Обеспечивают сопряжение винт-гайка через тела качения.

По числу рядов тел качения

Однорядные,

Двухрядные,

Многорядные;

По способности компенсировать несоосность вала и втулки[4]

Самоустанавливающиеся.

Несамоустанавливающиеся.

32 вопрос

Последовательность расчета (подбора) подшипников качения на долговечность

Исходные данные: 1. Расчетная схема вала с указа­нием значения и направления нагрузок

2.   Угловая скорость вала ω.

3.   Диаметр цапф вала d.

4.   Условия работы подшипникового узла.

Последовательность расчета: 1. Определяют

радиальные опорные реакции в вертикальной /?„ и горизонталь­ной RT плоскостях, а затем суммарные реакции Rr для каждой опоры:                                                        

При определении опорных реакций радиально-упорных под­шипников пролетом между опорами считают расстояние / с уче­том угла контакта α(рис. 24.15 и 24.16).

Тип подшипника выбирают исходя из условий работы, дей­ствующих нагрузок и намечаемой конструкции подшипниково­го узла.

2. По каталогу, ориентируясь на легкую серию, по диаметру цапфы подбирают подшипник и выписывают характеризующие его данные:

а) для шарикового радиального и радиально-упорного с уг­лом контакта α < 18° значения базовых динамической Сг и стати­ческой Cor радиальных грузоподъемностей;

б)  для шарикового радиально-упорного с а^ 18° значения Сг и по табл. 24.2 (или каталогу) значение коэффициента е\

в)   для конического роликового значения Сг, ей Υ.

3.   Для шариковых радиально-упорных и роликовых кониче­ских подшипников определяют для обеих опор осевые составляю­щие Rs от радиальных сил Rr [формулы (24.4) и (24.5) ], а затем по формулам табл. 24.3 вычисляют расчетные осевые силы Ra.

33вопрос

Расчет подшипников качения при статическом нагружении

Статическая грузоподъемность подшипника определяется как статическая радиальная нагрузка, которой соответствует общая остаточная деформация  тела качения и колец в наиболее нагруженной зоне контакта, равная 0,0001 диаметра тела качения.

В однорядных радиально-упорных подшипниках статическую грузоподъемность рассчитывают по радиальной составляющей нагрузки, вызывающей радиальное смещение колец подшипника относительно друг друга.

Для подшипников, которые работают при медленном вращении (n<1 об/мин), а также в режиме качательного движения, допустимая нагрузка определяется не усталостью материала, а остаточной деформацией на контактирующих рабочих поверхностях. Необходимо, чтобы величина действующей на подшипник нагрузки не превышала допустимую статическую грузоподъемность С0. В этом случае остаточная деформация мала и не снижает работоспособности подшипника.

Расчет неподвижного или медленно вращающегося (n<1 об/мин) подшипника производят по статической грузоподъемности С0. Если статическая нагрузка состоит из радиальной и осевой составляющих, то определяется эквивалентная статическая нагрузка. Эквивалентная нагрузка вызывает у подшипников такие же остаточные деформации, как и при действительных условиях нагружения.

Эквивалентная статическая нагрузка на радиально-упорные шарикоподшипники составляет

на упорно и упорно-радиальные шариковые и роликовые подшипники.

где Fr — наибольшая радиальная составляющая статической нагрузки,

34 вопрос(36вопрос одно и тоже)

5. ПРОВЕРОЧНЫЙ РАСЧЕТ ЗУБЬЕВ ЧЕРВЯЧНОГО КОЛЕСА НА ИЗГИБНУЮ ВЫНОСЛИВОСТЬ

Расчет на изгибную выносливость производиться по формуле

σF=1,54*YF К'*T2*cosγ/(m²*d2*q)

где σF -расчетное напряжение изгиба

σFР - допускаемое напряжение изгиба

К' - уточненное значение коэффициента нагрузки

Расчетная формула справедлива при любых взаимосогласованных единицах измерения. Целесообразно принять σF и σFР в Н/мм²(МПа);

m, d2 – в мм, T2 – в Н•мм

YF - коэффициент формы зуба, принимаемый по таблице 7, в зависимости от эквивалентного числа зубьев червячного колеса

Zγ= Z2/cos³γ.

Коэффициент формы зуба YF для червячных колес Таблица 7

Zγ	28	30	35	40	45	50	60	80	100	150
YF	1,80	1,76	1,64	1,55	1,48	1,45	1,40	1,34	1,30	1,27

Обычно расчетное напряжение изгиба червячных колес, размеры которых определены из расчета на контактную прочность, оказываются ниже допускаемых.

1.1 Выбор материалов для изготовления червяка и червячного колеса

Для червячных передач характерны следующие виды разрушения зубьев:

выкрашивание активных поверхностей зубьев;

излом зубьев червячного колеса у основания;

пластическая (остаточная) деформация зубьев червячного колеса при действии максимальной нагрузки;

заедание зубьев.

Для предотвращения разрушения зубьев червячного колеса (в червячной передаче червячное колесо является слабым звеном) выполняются соответствующие расчеты:

на контактную выносливость активных поверхностей зубьев;

на изгибную выносливость;

на предотвращения заедания (тепловой расчет);

для предотвращения остаточных деформаций проводят проверочные расчеты при действии кратковременных пиковых нагрузок.

С целью уменьшения влияния неблагоприятных факторов, имеющих место в зоне зацепления червячной передачи, следует применять для зубчатых венцов червячных колес материалы с высокими антифрикционными свойствами, уменьшать шероховатость активных поверхностей витков червяка, а также применять смазки с противозадирными присадками. Кроме того, для предотвращения заедания червяк и червячное колесо должны быть изготовлены из разнородных материалов. В зависимости от скорости скольжения и склонности к заеданию материалы, применяемые для изготовления зубчатых венцов червячных колес, подразделяются на три группы.

1-я группа:

бронзы высокооловянистые (с содержанием олова 6…10%), применяемые в ответственных высокоскоростных передачах при Vск ≤25 м/с. К этой группе относятся бронзы марок БрОФ10-1, БрОНФ и др.;

бронзы низкооловянистые (с содержанием олова 3…6%), применяемые в передачах Vск ≤12 м/с, так как их противозадирные свойства хуже, чем у высокооловянистых бронз. Сюда относятся бронзы марок БрОЦС6-6-3, БрОЦС5-5-5 и др.;

2-я группа:

безоловянистые бронзы (σв>350 МПа), применяемые в передачах с Vск ≤ 8 м/с. К этой группе относятся бронзы БрАЖ9-4Л, БрАЖН10-4-4Л и др., они дешевле, чем оловянистые, обладают достаточно хорошими антифрикционными свойствами.

Червяк, работающий в паре с этими бронзами, должен иметь твердость рабочих поверхностей не ниже НRC45;

3-я группа:

мягкие серые чугуны, применяемые для тихоходных малонагруженных передач с Vск ≤ 2 м/с (СЧ12-28, СЧ15-32, CЧ18-36, СЧ21-40).

2.2 Допускаемые напряжения для расчета на изгибную выносливость

Допускаемые напряжения изгиба для зубьев венцов колес, выполненных из материалов 1-ой и 2-ой групп (оловянистые и безоловянистые) определяются по формуле

σFP= σFO ,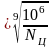

где σF – предел ограниченной изгибной выносливости бронзы при условном числе циклов нагружения N=106. При нереверсивной нагрузке величина предела ограниченной изгибной выносливости определяется по формуле

σFO=0,25σт+0,08σв

При реверсивной нагрузке

σFO=0,16σв

Здесь σт и σв – предел текучести и предел прочности бронзы соответственно (см.табл.1). При Nц>25•107 в исходную формулу следует подставлять Nц=25•107, при Nц<106 следует принимать Nц = 106. При этих условиях

0,543≤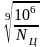 ≤ 1,0

Для червячных колес, выполненных из материалов 3-ей группы (чугуны), допускаемое напряжение для расчета на изгибную выносливость:

σFP=0,12σИ

– для нереверсивных передач;

σFP=0,075 σИ

– для реверсивных передач;

Здесь σИ – предел прочности чугуна при изгибе (см. табл.1).

2.3 Предельные допускаемые напряжения для расчета передачи при пиковых нагрузках

Предельные допускаемые напряжения σHPMAX и σFPMAX для расчета передачи при пиковых нагрузках вычисляются по формулам, приведенным в таблице 2.

Предельные допускаемые напряжения при пиковых нагрузках

Таблица 2

Материал	σHPMAX	σFPMAX
Оловянистые бронзы (1-я группа)	4σт	0,8σт
Безоловянистые бронзы (2-я группа)	2σт
Чугуны (3-я группа)	260…300 МПа	0,6σв

В таблице: σт – предел текучести материала;

σв – предел прочности чугуна при растяжении (см.табл.1)

3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА НАГРУЗКИ

Коэффициент нагрузки для червячных передач

К=Кβ•Кν,

где Кβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;

Кν – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении.

Коэффициент К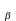 , главным образом, зависит от деформации червяка

К =1+(Z2/Q)3(1-X),

где Q-коэффициент, зависящий от характера изменения нагрузки. Значения коэффициента Q приведены в таблице 3.

Таблица 3. Значение коэффициента деформации червяка Q

Z1	Значение Q при q, равном
	7,5	8	9	10	11	12	13	14	16
1	63	72	89	108	127	147	163	179	194
2	50	57	71	86	102	117	134	149	163
3	46	51	61	76	89	103	118	131	144
4	42	47	58	70	82	94	108	120	137

При постоянной нагрузке Х=1, при незначительных колебаниях Х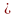 0,6 и при значительных - Х 0,3.

Поскольку зубья червячного колеса обладают способностью прирабатываться при постоянной нагрузке, то происходит их полная приработка и, следовательно концентрация нагрузки будет отсутствовать, поэтому можно принять Кβ=1,0

Коэффициент Кν зависит в основном от степени точности передачи и от скорости скольжения Vск в зацеплении (см. табл. 4). Для червячных передач установлено 12 степеней точности, обозначаемых в порядке убывания точности 1,2,3…,12. Для силовых передач предназначаются степени с 5 по 9-ю. Для редукторов общего назначения применяют в основном 7 и 8-ю степени точности. При скоростях скольжения, для которых в таблице 4 значения Кν не указаны, соответствующие точности изготовления передач не применяются. Таким образом, таблица 4 может быть также использована для назначения степени точности передачи.

35.Расчет линейчатых червячных передач на контактную выносливость

ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ

Червячные передачи относятся к зубчатым передачам с перекрещивающимися осями. Угол перекрещивания осей обычно составляет 90°. Червячную передачу целесообразно использовать там, где требуется плавность и бесшумность в работе, компактность при значительном редуцировании частоты вращения и сравнительно небольшой передаваемой мощности (обычно до 60 кВт). Значения передаточных чисел могут достигать до 1000. Однако в силовых передачах передаточное число рекомендуется выбирать в интервале значений от 8 до 80, реже до 110. Червячные передачи используются в подъемно-транспортных машинах, станках, автомобилях и других машинах.

Передача состоит из червяка и червячного колеса. Движение в червячной передаче преобразуется по принципу винтовой пары или по принципу наклонной плоскости. В червячной передаче ведущим звеном является червяк с числом заходов  , ведомым звеном – червячное колесо с числом зубьев  .

Достоинства червячной передачи:

– большие передаточные отношения в одной ступени;

– плавность и бесшумность работы;

– возможность самоторможения;

– высокая кинематическая точность.

Недостатки червячной передачи:

– низкий КПД, являющийся причиной большого тепловыделения, которое, в свою очередь, требует применения специальных устройств для отвода тепла (обдув, оребрение корпуса и т.д.);

– необходимость применения дорогостоящих цветных металлов;

– значительный износ;

– склонность передачи к заеданию.

Типы червяков и области их применения

В связи с изготовление червячных колес инструментом, являющимся аналогом червяка, сопряженный профиль зубьев червячного колеса получается автоматически. Поэтому профилем витков червяка можно варьировать. Выбор профиля витков червяка (типа червяка) определяется технологическими возможностями конкретного производства.

Различают два вида рабочей поверхности витков цилиндрических червяков:

– линейчатый, образуемый винтовым движением прямой линии;

– нелинейчатый, образуемый винтовым движением заданной кривой.

Благодаря технологичности наибольшее применение получили цилиндрические червяки с линейчатой винтовой поверхностью. Тип цилиндрического червяка с линейчатой винтовой поверхностью определяется формой профиля витков в торцевой плоскости   (рис. 6.1).

 

Рис. 6.1

Различают следующие типы цилиндрических червяков с линейчатой винтовой поверхностью: архимедов, конволютный и эвольвентный.

У архимедова червяка (ZA) теоретический торцовый профиль витков очерчен архимедовой спиралью. В осевом сечении   червяк имеет прямолинейный профиль витков, а в нормальном сечении  (см. рис. 6.1) – криволинейный. Архимедов червяк может быть нарезан на обычных токарных и резьбофрезерных станках. Однако для шлифования витков требуются специальные шлифовальные круги фасонного профиля, что затрудняет обработку и снижает точность передачи. Поэтому архимедовы червяки применяют в передачах при твердости материала червяка  .

Тип червяка на точность передачи не влияет, поэтому в приборостроении часто применяют простые в изготовлении архимедовы червяки.

У конволютного червяка (ZN) теоретический торцовый профиль витков очерчен по удлиненной (реже укороченной) эвольвенте. В осевом сечении червяк имеет криволинейный профиль витков, а в нормальном сечении – прямолинейный. Стандарт предусматривает три типа конволютных червяков. Конволютные червяки имеют некоторые технологические преимущества перед архимедовыми червяками, но для шлифования их витков также требуется специальное профилирование шлифовального круга. Поэтому в машиностроении конволютные червяки используются редко, в основном они используются в приборостроении.

У эвольвентного червяка (ZJ) теоретический торцовый профиль витков очерчен по эвольвенте круга. В осевом и нормальном сечениях червяк имеет криволинейный профиль витков. Эвольвентный червяк по существу представляет собой косозубое цилиндрическое зубчатое колесо с очень большим углом наклона зубьев, равным углу подъема витков   (см. рис. 6.2), и малым числом зубьев, равным числу заходов  .

Нагрузочная способность червяков всех типов является приблизительно одинаковой. Нагрузочная способность червячных передач повышается с увеличением твердости витков червяка ( ) и их последующим шлифованием. Шлифование после термообработки витков эвольвентного червяка не сопряжено с техническими трудностями, поскольку витки шлифуются плоской стороной шлифовального круга. Поэтому в быстроходных механизмах, работающих со значительными нагрузками, используются эвольвентные червяки.

Шлифование витков конволютного червяка конусными кругами с прямолинейной образующей на обычных резьбошлифовальных станках приводит к получению цилиндрических червяков с нелинейчатой винтовой поверхностью, весьма близкой к поверхностям витков конволютных червяков. Червячные фрезы для нарезания червячных колес шлифуют тем же способом, поэтому получают правильное зацепление. Нелинейчатые червяки изготавливают трех типов: ZK1, ZK2, ZK3.

Существует два вида цилиндрических червяков с вогнутым профилем витков (ZT1, ZT2), которые используются при необходимости обеспечения большой нагрузочной способности и высокого КПД. Передачи с вогнутым профилем витков червяка имеют лучшие условия для образования масляного клина, а также большие приведенные радиусы кривизны. Поэтому несущая способность таких передач на 30-60 % больше по сравнению с обычными цилиндрическими червячными передачами (большие значения – при больших скоростях); потери на трение в них до двух раз меньше.

Несущую способность червячных передач можно существенно повысить, если червяк выполнить глобоидным (см. параграф 3.5). При этом увеличиваются число зубьев червячного колеса   в зацеплении и приведенные радиусы кривизны, улучшаются условия образования масляных клиньев в зацеплении. Несущая способность глобоидных передач при условии точного изготовления и эффективного охлаждения до полутора раз больше по сравнению с цилиндрическими червячными передачами, имеющими линейчатую винтовую поверхность витков червяка.

Глобоидные передачи вследствие малых габаритов и, следовательно, малой поверхности теплоотдачи оказываются сильно напряженными в тепловом отношении, поэтому их применяют в повторно кратковременном режиме работы с искусственным охлаждением. Применение глобоидных передач более эффективно для передачи больших моментов.

Технология изготовления и сборки глобоидных передач существенно сложнее по сравнению червячными передачами с цилиндрическими червяками. При сборке необходима выверка точного положения вдоль оси не только червячного колеса, но и червяка.

При малых угловых скоростях и нагрузках применяют упрощенные червячные передачи, которые позволяют применять более прогрессивную технологию обработки червячных колес (штамповку) и червяков (навивку). Упрощенные червяки при   выполняют в виде цилиндрической пружины, затянутой на валу.

37.Силовые зависимости в червячных передачах

Червячная передача-механическое устройство для передачи вращения между скрещивающимися (обычно под прямым углом) валами посредством червяка (винта) и сопряжённого с ним червячного колеса. Червяк (см. рис. 2, в при ст. Детали машин)  представляет собой винт с трапецеидальной или близкой к ней резьбой (См. Резьба), а червячное колесо является зубчатым колесом (См.Зубчатое колесо), зубья которого имеют особую дугообразную форму. Червячное колесо охватывает червяк на некоторой дуге (обычно до 100°). Ведущим в Ч. и. является обычно червяк, ведомым — червячное колесо; в редких случаях (для повышающих передач) ведущим может быть червячное колесо. В наиболее распространённых Ч. п. используются цилиндрические червяки; червяки с витками на тороидной поверхности применяются в глобоидных передачах (См. Глобоидная передача). В зависимости от числа заходов резьбы (ниток нарезки) различают одно-, двух- и четырёхзаходные червяки; по форме профиля витка — архимедовы, с вогнутым профилем и др. червяки. Витки архимедовых червяков в осевом сечении очерчены трапецией и легко изготовляются точением. Перспективны червяки с вогнутым профилем витков резьбы, обеспечивающим меньшие контактные напряжения и лучшие условия для образования масляного клина. Для силовых передач (См. Силовая передача) предпочтительны эвольвентные червяки, профиль витка которых в поперечном сечении очерчен по эвольвенте (см. Эволюта и эвольвента).Передаточное число Ч. п. i = z2/z1, где z1 — число заходов резьбы червяка, z2 — число зубьев червячного колеса.

         Обычно передаточное число Ч. п. равно 8—100 (в ряде случаев, например в приводах станочных столов большого диаметра, до 1000). Благодаря возможности получения больших передаточных чисел при сравнительно небольшом габарите передачи Ч. п. применяются в Приводах машин, устройствах управления и др. Достоинства Ч. п. — плавность и бесшумность работы. Ч. п. могут быть самотормозящими, т. е. передающими вращение только от червяка к колесу, что иногда даёт возможность выполнить механизм без тормозного устройства. Недостаток Ч. п. — значительное относительное скольжение сопряжённых элементов — витков червяка и зубьев колеса. Это вызывает усиленное тепловыделение, повышенный износ и склонность к заеданию, определяет сравнительно низкий кпд (в среднем 0,7—0,75 в однозаходной передаче, 0,8— 0,85 в двухзаходной, 0,86—0,92 в четырёхзаходной). Для уменьшения износа и повышения сопротивляемости заеданию червячные колёса изготовляют из материалов с высокими антифрикционными свойствами, главным образом из бронзы: оловянистой (при скоростях скольжения 5—35 м/сек) и алюминиево-железистой (при скоростях скольжения до 10 м/сек). Для экономии цветных металлов их делают составными: бронзовый венец (обод) устанавливается на стальную или чугунную ступицу. При скоростях скольжения до 2 м/сек и больших диаметрах колёса можно отливать целиком из чугуна. В приборах и небольших силовых передачах могут использоваться колёса из текстолита, полиамидов и т.п. Червяки обычно изготовляют из качественных углеродистых или легированных сталей, термически обработанных до высокой твёрдости. Для повышения качества поверхности червяки шлифуют и полируют.

         Пониженный кпд и значительное тепловыделение ограничивают применение Ч. п. областью небольших и ср. мощностей (обычно до 50, реже до 200 квт). Они используются в подъёмно-транспортных машинах, металлорежущих станках, автомобилях, троллейбусах, металлургических машинах, гидротехнических сооружениях и т.д. Основное применение имеют закрытые хорошо смазываемые Ч. п. в виде червячных Редукторов.

ЧЕРВЯЧНАЯ ПЕРЕДАЧА - механизм для передачи вращения между скрещивающимися валами посредством винта (червяка) и сопряженного с ним червячного колеса. Применяется в силовых передачах, обеспечивает передаточное отношение до 300 и более.

41. силовые зависимости в конических передачах с круговыми зубьями

 На практике наиболее распространены конические колеса с тангенциальными и круговыми  зубьями.

 Тангенциальные зубья направлены по касательной к некоторой воображаемой окружности радиусом е и составляют с образующей конуса угол 25..300;

 Круговые зубья  располагаются по дуге окружности а, по которой движется инструмент при нарезании зубьев. Угол наклона зубьев переменный, под расчетным принимают угол на окружности среднего  диаметра колеса, как угол между касательной к окружности и образующей конуса в данной точке 350

 Чаще всего применяются колеса с круговыми зубьями, которые менее чувствительны к нарушениям точности взаимного расположения колес и более просты в изготовлении.

 Нагрузочная способность колес с непрямыми зубьями выше в 1,4...1,5 раза по сравнению с прямыми.

Силы в зацеплении

окружная  радиальная  осевая 

Знак «+» в случае совпадения направления крутящего момента  и винтовой линии зуба при наблюдении со стороны внешнего торца.

42. Расчет зуба конической прямозубой передачи на изгибную выносливость.

Допускаемые напряжения на изгибную выносливость   определяют по формуле:  МПа, где:  - предел изгибной выносливости, МПа; определяют в зависимости от твердости материала HB:  МПа,   - коэффициент запаса изгибной прочности;   - коэффициент долговечности; рассчитывают по зависимости:  , здесь   - базовое число циклов.  Диапазон значений   находится в пределах:  . Т.к. рассчитанный коэффициент  , то принимаем  . 

При проверочном расчете конических зубчатых передач на выносливость при изгибе условия прочности выглядят в виде:

;

,

где   – динамический коэффициент при проверочном расчете на выносливость при изгибе, определяемый по аналогии с коэффициентом  ;   – коэффициенты формы зуба, соответственно, шестерни и колеса, определяемые в зависимости от эквивалентного числа зубьев шестерни   и колеса 

43. Расчет зуба конических прямозубых передач на контактную выносливость.

Допускаемые напряжения на контактную выносливость   определяют по формуле:  МПа, где:  - предел контактной выносливости, МПа; определяют по зависимости:  МПа;   - коэффициент запаса контактной прочности;   - коэффициент долговечности; рассчитывают по зависимости:  , здесь   - базовое число циклов:  Диапазон значений   находится в пределах:  . Т.к. рассчитанный коэффициент  , то принимаем  При проверочном расчете конических зубчатых передач на контактную выносливость условие прочности выглядит в виде:

,

где   – крутящий момент на валу колеса, Н·м;   – динамический коэффициент при проверочном расчете на контактную выносливость, определяемый в зависимости от окружной скорости колес и степени точности (окружная скорость определяется на среднем делительном диаметре колеса  );   – внешний делительный диаметр колеса, мм.

44. Геометрия и кинематика конических передач с круговыми зубьями.

Конические передачи (рис. 9.9) передают вращающий момент между валами, оси которых пересекаются. Будем рассматривать передачи с межосевым углом 90°; эти передачи называют ортогональными. Наибольшее распространение получили передачи с прямыми (рис. 9.9, б) и круговыми (рис. 9.9, в) зубьями. Углы делительных конусов обозначают для шестерни 6i и для колеса 62.

а

А-А

А-А

Рис. 9.9. Коническое зубчатое зацепление при б+б2=90о:

о — основные параметры и схема передачи: / — внешний делительный конус; 2 — внешний делительный дополнительный конус; б — прямые зубья; в — косые зубья

Коническая поверхность, образующие которой соответственно перпендикулярны к образующим делительного конуса, называется делительным дополнительным конусом. Конусы / и 2 пересекаются по окружности, которую называют делительной окружностью. Конусы / и 2 пересекаются по окружности, которую называют делительной окружностью. Диаметры de и d соответственно являются диаметрами внешней и средней делительных окружностей. Шаги на этих окружностях pte и pt называются соответственно внешним и средним окружными шагами; их отношение к я — внеш-

2

ним mte (или те для прямозубых передач) и средним т модулями. В прямозубых передачах расчет обычно ведут по внешнему окружному модулю те*, а в передачах с круговым зубом — по среднему нормальному модулю тп = mte(RlRe) cos рп, где R и Re называются соответственно средним и внешним делительными конусными расстояниями (см. рис. 9.9, а); рте — угол наклона кругового зуба в середине ширины зубчатого венца. Обычно принимают рп=35°.

Отношение ширины зубчатого венца Ь к внешнему делительному конусному расстоянию Re называется коэффициентом ширины зубчатого венца: tybe—b/Re.

Сечение делительного конуса делительным дополнительным конусом образует торцевое сечение, в котором профиль зубьев конических передач близок к эвольвентному. Поэтому при расчетах конических колес используют параметры эвольвентных цилиндрических прямозубых передач с эквивалентным числом зубьев zv (рис. 9.10).

Диаметр делительной окружности эквивалентного колеса (см. треугольник OKN и развертку дополнительного конуса)

dve—de/cos д = mez/cos 6 = mezv.

Эквивалентное число зубьев

z„ = 2:/cos6,(9.6)

где z — действительное число зубьев конического колеса. Для шестерни рекомендуют принимать z\ = 18...24.

* Модули рекомендуют устанавливать по ГОСТ 9563—60. Но в то же время допускается использовать дробные и нестандартные значения, если это не влечет за собой необходимости применения специального инструмента.

45. Силы в зацеплении конической передачи

Силы в зацеплении определяют по размерам в среднем сечении зуба шестерни. На шестерню конической прямозубой передачи действуют три силы рис.2.3.19: окружная   (2.3.58),  радиальная   (2.3.59), осевая   (2.3.60).

Рисунок 2.3.19 Схема действия сил в зацеплении конических колес

Для колеса направление сил противоположно, при этом:

; ;

Направление окружных сил F, как и в цилиндрической передаче зависит от направления вращения колёс. Осевые силы  всегда направлены от вершин конусов, радиальные   - к осям вращения колёс. Конические передачи с круговыми зубьями получили преимущественное применение. По сравнению с коническими прямозубыми они менее чувствительны к нарушению точности взаимного расположения колёс, их изготовление проще. Недостаток передач с круговыми зубьями – изменение величины и знака осевых сил при реверсе. Ось кругового зуба – это дуга окружности соответствующего диаметра резцовой головки. Нарезание зубьев резцовой головки обеспечивает высокую производительность и низкую стоимость колёс. Угол наклона кругового зуба переменный. За расчётный принимают угол на окружности среднего диаметра колеса, обычно Значение выбирают исходя из обеспечения плавности зацепления.

46.Геометрические параметры конического зубчатого колеса

Основные геометрические размеры определяют в зависимости от модуля и числа зубьев. Высота и толщина зубьев конических колёс постепенно уменьшается по мере приближения к вершине конуса. Соответственно изменяются шаг, модуль и делительные диаметры, которых может быть бесчисленное множество. Основные геометрические размеры имеют обозначения, принятые для прямозубых конических передач рис. 2.3.18.

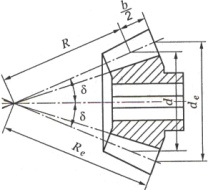Рисунок 2.3.18 Геометрия конического колеса

Внешний диаметр   :

(2.3.45)

где   - максимальный модуль зубьев – внешний окружной модуль, полученный по внешнему торцу колеса. Внешнее конусное расстояние (2.3.46)

Среднее конусное расстояние   (2.3.47), где b – ширина зубчатого венца колеса

(2.3.48)

 - коэффициент ширины зубчатого венца относительно внешнего конусного расстояния. - углы делительных конусов; Средний модуль

(2.3.49)

Средние делительные диаметры:

(2.3.50)

(2.3.51)

В соответствии с исходным контуром прямозубых конических колёс радиальный зазор c = 0,2  , тогда  внешняя высота головки зуба  (2.3.52) и внешняя высота ножки зуба  (2.3.53).  Внешние диаметры вершин зубьев (2.3.54)

(2.3.55)

Угол ножки зуба  (2.3.56). Угол головки зуба   ;  (2.3.57)

Геометрические параметры

 Аналогом начальных и делительных цилиндров являются начальные и делительные конусы. Конусы, образующие которых перпендикулярны к образующим делительных конусов, называются дополнительными конусами.

 Сечение зуба дополнительным конусом называется торцевым сечением. Различают внешнее  (e), внутреннее и среднее (m) сечения. Размеры по внешнему торцу более удобны для замеров, их указывают на чертежах. Размеры в среднем сечении используют в силовых расчетах.

 Зависимости размеров в среднем и торцевом сечениях  (для прямозубых колес нормальное (n) и торцевое (t) сечения совпадают):

внешнее конусное расстояние        

делительный диаметр колеса                   

торцевой модуль во внешнем сечении

 Для прямозубых передач нормальное и торцевое сечения совпадают, поэтому   округляют по ГОСТ 9563-80.

47. Расчет зуба цилиндрической косозубой передачи на изгибную выносливость.

Проверочный расчет зубьев на изгибную выносливость

. Видом разрушения является усталостная поломка зуба. Критерий расчета - изгибная выносливость. Условие работоспособности по критерию выносливости может быть записано в виде

F [F],

где F - фактическое напряжение изгиба, Н/мм2; [F] - допускаемое напряжение изгиба, Н/мм2.

Допускаемое напряжение изгиба на шестерне и колесе найдем по формуле

где [SF] - коэффициент безопасности по изгибу;

KFL - коэффициент долговечности;

KFC - коэффициент, учитывающий влияние двухстороннего приложения нагрузки;

F lim b - базовый предел изгибной выносливости.

Учитывая, что твердость зубчатого колеса HB2=280, следовательно, по рекомендации выбираем F lim b=1,8·HB2=1,8·280=504 Н/мм2.

Так как приложение нагрузки одностороннее выбираем KFC = 1.

Коэффициент безопасности по изгибу вычисляется по формуле

[SF] = [SF] '· [SF] '', (1.45)

где [SF] ' - коэффициент, учитывающий нестабильность свойств материала; [SF] '' - коэффициент, учитывающий способ получения заготовки.

По рекомендации определяем [SF] '=1,75.

В соответствии с рекомендациями выбираем [SF] ''=1.

Подставляя численные значения коэффициентов в выражение (1.45), получаем численное значение коэффициента безопасности по изгибу

[SF] =1·1,75=1,75.

Определим коэффициент долговечности для шестерни и колеса по формуле

(1.46)

где NFO - базовое число циклов; NFE - фактическое число циклов.

Принимаем базовое число циклов NFO = 4·106. Фактическое число циклов определяется из соотношения

NFEi = NHei, (1.47)

NHE1=8,3·107

NHE2 =2·107

Вычислим численные значения допускаемых напряжений изгиба на шестерне и колесе

Для определения на шестерне или на колесе произойдет поломка зуба, следует сравнить следующие отношения

где YF1 - коэффициент, учитывающий форму зуба шестерни; YF2 - коэффициент, учитывающий форму зуба колеса.

Коэффициент, учитывающий форму зуба, вычисляется по ГОСТ 21354-75 в зависимости от коэффициента смещения

где z1 - коэффициент смещения.

Вычислим коэффициент смещения для шестерни

С учетом интерполяции при z1 = 21,9, YF1=4,09. Вычислим численное значение отношения (1.48) для шестерни

Н/мм2.

Вычислим коэффициент смещения для колеса

С учетом интерполяции при z2=87,6, YF2 = 3,61.

Вычислим численное значение отношения (1.48) для колеса

Подставим в выражение (4.48) численные значения отношений

Так как отношение для шестерни оказалось меньше, чем для колеса, следовательно, первым зуб сломается на шестерне.

Сделаем проверочный расчет для косых зубьев шестерни

F [F

Фактическое напряжение изгиба на шестерне можно вычислить по формуле

(1.51)

где Ft1 - окружная сила, Н; KF - коэффициент нагрузки; Y - коэффициент учитывающий угол контактных линий; KF - коэффициент, учитывающий неравномерность распределения нагрузки между зубьями.

В соответствии с рекомендациями, принимаем коэффициент, учитывающий неравномерность распределения нагрузки между зубьями KF=0,92.

Окружная сила вычисляется по формуле

Вычислим численное значение окружной силы

Н

Коэффициент нагрузки вычисляется по формуле

KF=KF·KF,

где KF - коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба; KF - коэффициент, учитывающий динамическое действие нагрузки.

Динамический коэффициент KF=1, а для определения коэффициента концентрации нагрузки следует вычислить bd по формуле.

Подставляя численные значения в выражениенайдем bd

Следовательно, по таблице при bd=0,5 и симметричном расположении зубчатых колес, KF=1,05. Подставив численные значения коэффициента концентрации нагрузки и коэффициента динамичности в выражение в (1.53), получим численное значение коэффициента нагрузки

KF=1·1,05=1,05.

Коэффициент, учитывающий угол контактных линий, определяется по формуле

Вычислим численное значение коэффициента, учитывающего угол контактных линий

Вычисляем численное значение фактического напряжения изгиба, подставляя численные значения окружной силы, коэффициента нагрузки, коэффициента, учитывающего угол контактных линий и коэффициента, учитывающего неравномерность распределения нагрузки между зубьями в

Так как фактическое напряжение изгиба зубьев на шестерне оказалось меньше допускаемого, следовательно, модуль передач оставляем без изменений

48. Расчет цилиндрических косозубых передач на контактную выносливость

 Проверочный расчет зубьев на контактную выносливость

. Основной причиной выхода их из строя служит усталостное выкрашивание. Следовательно, критерием проверочного расчета является контактная выносливость. Условие работоспособности по критерию выносливости может быть записано в виде

H [H],

где H - фактическое контактное напряжение, Н/мм2.

Фактическое контактное напряжение можно вычислить по формуле

(1.39)

где zH - коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления; z - коэффициент, учитывающий суммарную длину контактных линий. KH - вычисляем по формуле

KH = KH·KH·KH,

Где KH - коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;

KH - коэффициент динамичности. Запишем формулу для линейной скорости шестерни

где 1 - линейная скорость шестерни, м/с.

Вычислим численное значение линейной скорости шестерни

Так как передача является быстроходной (выбираем 8 степень точности) и линейная скорость шестерни менее 5 м/с, то по рекомендации выбираем KH=1,09.

Так как линейная скорость шестерни менее 5 м/с и передача является быстроходной (выбираем 8 степень точности), то по рекомендации выбираем KH=1,0.

Подставив численные значения коэффициентов в выражение (1.40), найдем KH

KH = 1,09·1,1·1,0=1, 199.

Коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, вычисляется по формуле

Для вычисления zH в соответствии с рекомендациями выбираем =20 и z=0,8, тогда подставляя численные значения в выражение (1.42), получаем

Подставляя численные значения в выражение (1.39), находим величину фактического контактного напряжения

Фактическое контактное напряжение оказалось меньше допускаемого

49 Силовые зависимости в цилиндрических косозубых передачах

Силы в зацеплении определяют в полюсе зацепления. Сила  , действующая на зуб косозубого колеса рис. направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса и составляет угол   с касательной к эллипсу. 

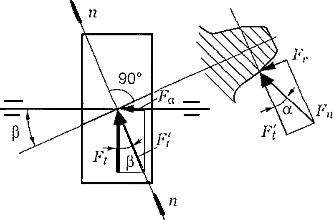Рисунок 2.3.16 Схема действия сил в зацеплении косозубых колес

Разложим эту силу на две составляющие: окружную силу на эквивалентном колесе радиальную силу на этом колесе:  Переходя от эквивалентного к косозубому колесу, заметим, что сила   является радиальной силой   и для этого колеса, т.е.

сила Ft расположена в плоскости, касательной к начальному цилиндру, и составляет угол   с осью колеса. Разложим силу Ft на две составляющие: окружную силу и осевую силу  Окружная сила известна. Её определяют по передаваемому моменту и диаметру делительной окружности зубчатого колеса  Тогда из формулы (2.3.35):  следует   Подставив силу   и выражения   , окончательно получим: радиальную силу    и осевую силу    На зубья шестерни и колеса действуют одинаковые, но противоположно направленные силы. При определении их направления учитывают направление вращения колёс и направление наклона линии зубьев   (правое и левое). Наличие в зацеплении осевой силы, которая дополнительно нагружает валы и подшипники, является недостатком косозубых передач.

50. Геометрия и кинематика косозубых цилиндрических передач

Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном диаметре, называют косозубыми. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение рис. 2.3.14. 

; Рис. 2.3.1 Цилиндрическая косозубая а) и шевронная б) передача

С увеличением угла наклона   линии зуба плавность зацепления и нагрузочная способность передачи увеличиваются рис.2.3.15, но при этом увеличивается и осевая сила Fа, что нежелательно. Поэтому в косозубых передачах принимают угол   .

Рисунок 2.3.15 Геометрия косозубых колес

Основные геометрические размеры зависят от модуля и числа зубьев. При расчёте косозубых колёс учитывают два шага: нормальный шаг зубьев pn - в нормальном сечении,  окружной шаг pt – в торцовом сечении; при этом    Соответственно шагам имеем два модуля зубьев:  (2.3.22)  (2.3.23) при этом  (2.3.24)

где mt и mn – окружной и нормальный модули зубьев.  За расчётный принимают модуль mn, значение которого должно соответствовать стандартному. Это объясняется следующим: для нарезания косых зубьев используется тот же инструмент, что и для прямозубых, но с соответствующим поворотом инструмента относительно заготовки на угол   . Поэтому профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба; следовательно, mn=m. Диаметры делительный и начальный

(2.3.25)

Диаметры вершин и впадин зубьев

(2.3.26) (2.3.27)

Межосевое расстояние

(2.3.28)

4.5.2 Эквивалентное колесо

Профиль косого колеса в нормальном сечении n-n (рис. 3) соответствует исходному контуру инструментальной рейки и, следовательно, совпадает с профилем прямозубого колеса.  Расчет косозубых колес проводят через параметры эквивалентного прямозубого колеса. Нормальное к линии зуба сечение делительного цилиндра имеет форму эллипса. Радиус кривизны эллипса при зацеплении зубьев в полюсе   профиль зуба в этом сечении достаточно близко совпадает с профилем приведённого прямозубого колеса, называемого эквивалентным,профиль зуба в этом сечении достаточно близко совпадает с профилем приведённого прямозубого колеса, называемого эквивалентным.  Делительный диаметр:  (2.3.29) эквивалентное число зубьев:   (2.3.30) или   (2.3.31) где z – действительное число зубьев косозубого колеса. С увеличением возрастает   возрастает   . Это одна из причин повышения прочности косозубых передач.

4.5.3 Силы в зацеплении

Силы в зацеплении определяют в полюсе зацепления. Сила  , действующая на зуб косозубого колеса рис. 2.3.16, направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса и составляет угол   с касательной к эллипсу. 

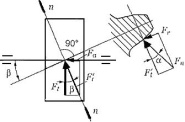Рисунок 2.3.16Схема действия сил в зацеплении косозубых колес

Разложим эту силу на две составляющие: окружную силу на эквивалентном колесе:  (2.3.22)  радиальную силу на этом колесе:   (2.3.33) Переходя от эквивалентного к косозубому колесу, заметим, что сила   является радиальной силой   и для этого колеса, т.е.

сила Ft расположена в плоскости, касательной к начальному цилиндру, и составляет угол   с осью колеса. Разложим силу Ft на две составляющие: окружную силу   (2.3.35), и осевую силу   (2.3.36). Окружная сила известна. Её определяют по передаваемому моменту и диаметру делительной окружности зубчатого колеса  (2.3.37) Тогда из формулы (2.3.35):  следует   Подставив силу   и выражения   ,  окончательно получим: радиальную силу   (2.3.38)  и осевую силу   (2.3.39). На зубья шестерни и колеса действуют одинаковые, но противоположно направленные силы. При определении их направления учитывают направление вращения колёс и направление наклона линии зубьев   (правое и левое). Наличие в зацеплении осевой силы, которая дополнительно нагружает валы и подшипники, является недостатком косозубых передач.

4.5.4. Расчет на контактную прочность

Вследствие наклона зубьев в зацеплении одновременно находится несколько пар зубьев, что уменьшает нагрузку на один зуб, повышая его прочность (снижая расчётные напряжения). Аналогично расчету прямозубой передачи межосевое расстояние для косозубых колес определяют по формуле (2.3.17):

,

где Ка = 43 МПа – для косозубых колес. Контактные напряжения в поверхностном слое зубьев

,

где   - коэффициент нагрузки при расчете по контактным напряжениям; - 1,04 – 1,13 коэффициент нагрузки, учитывающий распределение нагрузки между зубьями и зависит от окружной скорости;   - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий); для косозубых передач выбирается с учетом расположения колеса на валу и термообработки;  - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки  =1,02-1,06 при любой твердости, скорость до 10 м/с,  =1,1 при твердости поверхности не больше 350 НВ и скорости 10-20 м/с,  =1,05 при твердости более 350 НВ и скорости 10-20 м/с. Косозубые передачи работают более плавно, чем прямозубые, поэтому коэффициент   , меньше.  Условие контактной прочности косозубой передачи 

,

Если условие не выполняется, то изменяют ширину венца колеса b2, не выходя за пределы рекомендуемых значений . Если это не даст желательного результата, то либо назначает другие материалы колёс или другую термообработку, и расчёт повторяют. Расчет допускаемых напряжений ведется аналогично расчету прямозубых колес

4.5.5 Расчёт зубьев на изгиб

Наклонное расположение зубьев увеличивает их прочность на изгиб и уменьшает динамические нагрузки. Это учитывается введением в расчётную формулу прямозубых передач поправочных коэффициентов   и  . Формула проверочного расчёта косозубых передач

(2.3.41),

где YF - коэффициент формы зуба выбирают по эквивалентному числу зубьев zv;   - коэффициент, учитывающий наклон зуба;  - коэффициент распределения нагрузки по ширине венца определяют по аналогии с прямозубыми передачами;   = 0,81-0,91 - коэффициент распределения нагрузки между зубьями;   - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки   =1,2 при твердости зубьев не больше 350НВ,  = 1,1 при твердости зубьев более 350 НВ. Нормальный модуль зубьев mn определяют по аналогии с прямозубыми передачами. При некоторых средних значениях коэффициентов получим формулу для приближенного определения модуля косозубых передач

(2.3.42),

и для шевронных передач

(2.3.43),

При проверке по формуле (2.3.41):   можно получить   значительно меньше   , что не является недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб.Если расчётное значение   превышает допускаемое, то применяют колёса, нарезанные с положительным смещением инструмента, или увеличивают m;  >  означает, что в передаче из данных материалов решающее значение имеет не контактная прочность, а прочность зубьев на изгиб. На практике к таким передачам относятся передачи с высокой твёрдостью рабочих поверхностей зубьев – 51…63HRCэ (цементация, нитроцементация, азотирование). Проектировочный расчёт таких передач следует выполнять с целью обеспечения прочности зубьев на изгиб по форме определения минимально допустимого модуля m, а затем выполнить проверочный расчёт зубьев на контактную прочность.

51 вопрос.

Расчетное изгибное напряжение при номинальной нагрузке определяем по формуле

= = ,

где - коэффициент, учитывающий распределение нагрузки по ширине венца;

- коэффициент динамичности нагрузки.

Принимается: = 2=3,6 (см. выше)

при = =0,27, = 1,2 [3, табл. 20]

56 [3, табл. 21]

0,016 (зубчатые колеса прямозубые) [3, табл. 22]

= ==14 ,

принимаем =14 (т.к. не превышает величину ); [3, табл. 23]

= = =112,4 ;

= = 1,12.

Остальные данные см. проектировочный расчет.

= = 175 МПа.

175<213 – изгибная выносливость обеспечена.

52 вопрос.Кинематический и силовой расчеты зубчатой передачи.

Расчетная окружная скорость v, м/с, цилиндрической передачи

конической передачи

где ω — угловая скорость зубчатого колеса, рад/с; n — частота вращения зубчатого колеса, мин-1; dw — начальный диаметр цилиндрического зубчатого колеса, м; dwm — начальный средний диаметр конического зубчатого колеса, м.

Учитывая, что скорость точек начальных окружностей, находящихся в зацеплении зубчатых колес, одинакова, имеем v=ω1dw1/2=ω2dw2/2. Выражая диаметры dw1 и dw2 через модуль и соответствующие числа зубьев, получаем v=ω1(mz1/2)=ω2(mz2/2). Отсюда передаточное отношение i пары зубчатых колес (для одноступенчатой передачи) с учетом формулы

где ω1, n1, dw1 z1 и T1 — соответственно угловая скорость, частота вращения, начальный диаметр, число зубьев и крутящий момент ведущего зубчатого колеса; ω2, n2, dw2 z2 и T2 - то же, ведомого зубчатого колеса; η — к. п. д. передачи.

Так как для конической зубчатой передачи передаточное отношение см. предыдущую формулу

то, как следует из рис.

где δ1 - для ведущего, а δ2 - для ведомого зубчатого колеса.

Отношение числа зубьев z2 колеса к числу зубьев z1 шестерни называется передаточным числом зубчатой передачи u.

Таким образом,

Если ведущим зубчатым колесом является шестерня, то для такой передачи передаточное отношение и передаточное число представляют собой одну и ту же величину. Рекомендуемые максимальные значения передаточного числа одноступенчатой зубчатой передачи:

Цилиндрической в закрытом корпусе: ≤12,5

Конической в закрытом корпусе: ≤6,3

Открытой: ≤15

Средние значения коэффициента полезного действия одноступенчатой зубчатой передачи на подшипниках качения в зависимости от конструкции и степени точности.
	Закрытая 6-6 и 7-й степеней точности с жидкой смазкой	Закрытая 8-й степени точности с жидкой смазкой	Открытая с густой смазкой
Цилиндрическая	0,98	0,97	0,96
Коническая	0,97	0,96	0,94

Рис. 1

Окружная сила зубчатой передачи Ft: цилиндрической (рис. 1)

конической (рис. 2)

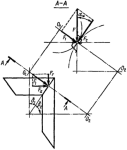
Рис. 2

Передаваемые зубчатыми колесами крутящие моменты определяют по формулам

и

.

Так как силы трения между зубьями малы, то силу давления между ними F можно считать направленной по общей нормали к соприкасающимся поверхностям зубьев, т. е. по линии зацепления (см. рис. 1). Составляющие этой силы: в цилиндрических прямозубых (рис. 1) и шевронных передачах - окружная сила Ft и радиальная сила Fr; в конической прямозубой (рис. 2) и цилиндрической косозубой (рис. 3) передачах - окружная сила Ft радиальная сила Fr, и осевая сила Fa.

Рис. 3

Радиальная сила, действующая на зубчатое колесо прямозубой цилиндрической передачи(рис. 1),

косозубой (рис. 3), или шевронной, передачи

конической прямозубой передачи (рис. 2)

Осевая сила, действующая на зубчатое колесо: цилиндрической косозубой передачи (рис. 3)

конической прямозубой передачи (рис. 2)

Сила давления между зубьями прямозубой цилиндрической передачи (рис. 1)

53 вопрос.

Цилиндрические зубчатые передачи. Краткие сведения по геометрии и кинематике

(или частоты вращения щ и п2 в мин-1), окружная скорость на делительном цилиндре ν в м/с, вращающие моменты 7] и Т2 в Η·μ,передаточное отношение и, коэффициент полезного действия η . При расчете передачи используются зависимости, известные из теоретической механики;    Передачи могут быть понижающие (частота вращения веду­щего вала больше ведомого) и повышающие. 11.2. Цилиндрические зубчатые передачи. Краткие сведения по геометрии и кинематике Зацепление зубчатых колес эквивалентно качению без скольжения окружностей с диаметрами dwX и dw2 (рис. 11.2). Эти окружности называются начальными. Точка их касания Π называется полюсом зацепления. Полюс лежит на линии, соеди­няющей оси колес О, и 02. Расстояние между осями колес aw называется межосевым расстоянием. Из зависимостей для межосевого расстояния aw и переда­точного отношения и диаметры начальных окружностей выражаются формулами Знак «-» — для внутреннего зацепления (см. рис. 11.1, г). Основным кинематическим условием, которому должны удовлетворять профили зубьев, является постоянство передаточ­ного отношения « = а>|/<й2 = dw2/dw] . При этом нормаль N{N2 к профилям зубьев в точке контакта К должна проходить через полюс зацепления. Этому условию удовлетворяют многие классы кривых (эвольвента, циклоида и др.). Эвольвеитное зацепление получило наибольшее распро­странение из-за преимуществ перед другими. Зубчатые колеса нарезают простым инструментом; при этом используется один и тот же инструмент независимо от числа зубьев колеса. Эвольвента окружности образуется точками К прямой N]N2 при качении ее без скольжения по окружностям с диаметрами db] илиdb2 (см. рис. 11.2). Эти окружности называются основ­ными. Линия N\N2 перемещения общей точки контакта К профи­лей зубьев при вращении колес называется линией зацепления. Угол ат, между линией зацепления и прямой, перпендикулярной межосевой линии, называется углом зацепления. Линия зацепления всегда является касательной к основным окружностям dh[ =dwi cosant, и db2 =rfw2cosatw ■При изменении межосевого расстояния, например, из-за ошибок изготовления, вместе с осями колес переместятся и основные окружности.

54 вопрос.

Расчет цилиндрической прямозубой передачи на контактную прочность 3.43. Расчет прочности контактирующих поверхностей зубьев основан на ограничении наибольших нормальных напряжений. При выводе формул приняты следующие допущения: зубья рассматри­вают как два находящихся в контакте цилиндра с параллельными образую­щими (радиусы этих цилиндров принимают равными радиусам кривизны профилей зубьев в полюсе зацепления); нагрузку считают равномерно рас­пределенной по длине зуба; контактирующие профили предполагают не­разделенными масляной пленкой. На основании этих допущений к расчету зубчатых колес можно приме­нить результаты исследований на контактную прочность цилиндрических роликов. Наибольшие нормальные контактные напряжения возникают в точках, лежащих на очень малой глубине под линией контакта по формуле Герца—Беляева:  (3.16) где q — расчетная удельная нормальная нагрузка; Епр — приведенный мо­дуль упругости материалов зубьев; ?пр — приведенный радиус кривизны профилей зубьев шестерни и колеса; ц — коэффициент Пуассона. Для прямозубых колес без учета коэффициентов нагрузки q = Fт /l?, (3.17) где Fn = F,/cosa? — нормальная сила, действующая на зуб (см. рис. 3.35); Ft — окружная сила; l? = b?K??a — суммарная длина контактной линии (для прямозубых передач 1? = Ь? — ширина венца, так как K??a ?1,0; здесь К? = 0,95 — коэффициент, учитывающий непостоянство суммарной длины контактной линии); ?a — коэффициент перекрытия. Для учета неравномерности распределения нагрузки по длине контакт­ных линий, а также для учета динамических нагрузок вследствие погреш­ности изготовления и деформации деталей передачи вводят коэффициент нагрузки К= КН?КНV (см. табл. 3.4—3.5). Отсюда  (3.18) Приведенный модуль упругости Епр = 2Е1Е2/(Е1 + Е2), где Ех и Е2 — мо­дули упругости материалов шестерни и колеса. Зубья рассматриваются как цилиндры длиной Ьа (ширина зубчатого ко­леса) и радиусов ?1 и ?2, где ъ Приведенный радиус кривизны зубьев в полюсе Здесь знак «плюс» для внешнего зацепления, знак «минус» — для внут­реннего зацепления.  Подставляя значения ?пр и q в формулу (3.17), после преобразований получим  (3.19) Обозначим в формуле (3.19) выражение  через ZH — коэффи­циент, учитывающий форму сопряженных поверхностей зубьев; = Zм — коэффициент, учитывающий механические свойства материалов сопряженных колес (ZM = 275 МПа1/2 — для стальных колес); = Zz — коэффициент, учитывающий суммарную длину контактных линии для прямозубых передач. Получим расчетную формулу, рекомендуемую для проверочного расчета:  (3.20) После подстановки значений Ft= 2T2/d1u; d1 = 2a?/(u  1) и b? =?ibaaw в формулу (3.20) и некоторых преобразований получим удобную для расчета формулу  (3.21) Значение ?Ьа определяют по формуле ?Ьа = 2?ba/(u+ 1) (?bd — см. табл. 3.7). Расшифруйте формулу (3.21) и подставьте единицы измерения парамет­ров, входящих в эту формулу. 3.44. После некоторых преобразований формулы (3.21) получим формулу проектировочного расчета для определения межосевого расстояния прямозу­бых зубчатых передач: Обозначим  через вспомогательный коэффициент Ка (для прямозубых передач при KHv = 1,25, Ка = 49,5 МПа1/3). Тогда формула проектного расчета для определения межосевого рас­стояния закрытых цилиндрических передач