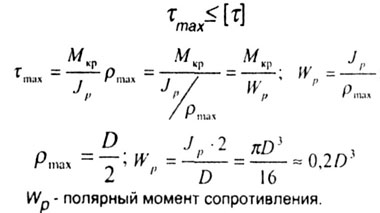- •Основные определения сопротивлений материалов.
- •Деформации перемещения, напряжения. Метод сечений
- •Растяжения и сжатия. Определение внутренних усилий, напряжений, перемещений.
- •Определение напряжений в наклонных сечениях. Определение главных напряжений и главных площадок.
- •4. Диаграммы растяжения и сжатия. Допускаемые напряжения. Основные типы задач при рассчете на прочность, растянутых (сжатых) стержней.
- •5.Сдвиг. Напряженное состояние и деформация при чистом сдвиге. Практич. Расчеты на сдвиг.
- •Геометрические харак-ки сечения. Изменение моментов инерции при парал-ном переносе и повороте осей.
- •7.Кручение. Определение напряжений и деформаций при кручении вала.
- •8.Изгиб. Определение внутренних усилий при изгибе. Зависимость между изгибающим моментом, поперечной силой и интенсивностью распред. Нагрузки.
- •9. Определение нормальных и касательных напряжений при изгибе.
- •10. Сложное сопротивление. Косой изгиб. Изгиб с растяжением. Внецентренное сжатие (растяжение).
4. Диаграммы растяжения и сжатия. Допускаемые напряжения. Основные типы задач при рассчете на прочность, растянутых (сжатых) стержней.


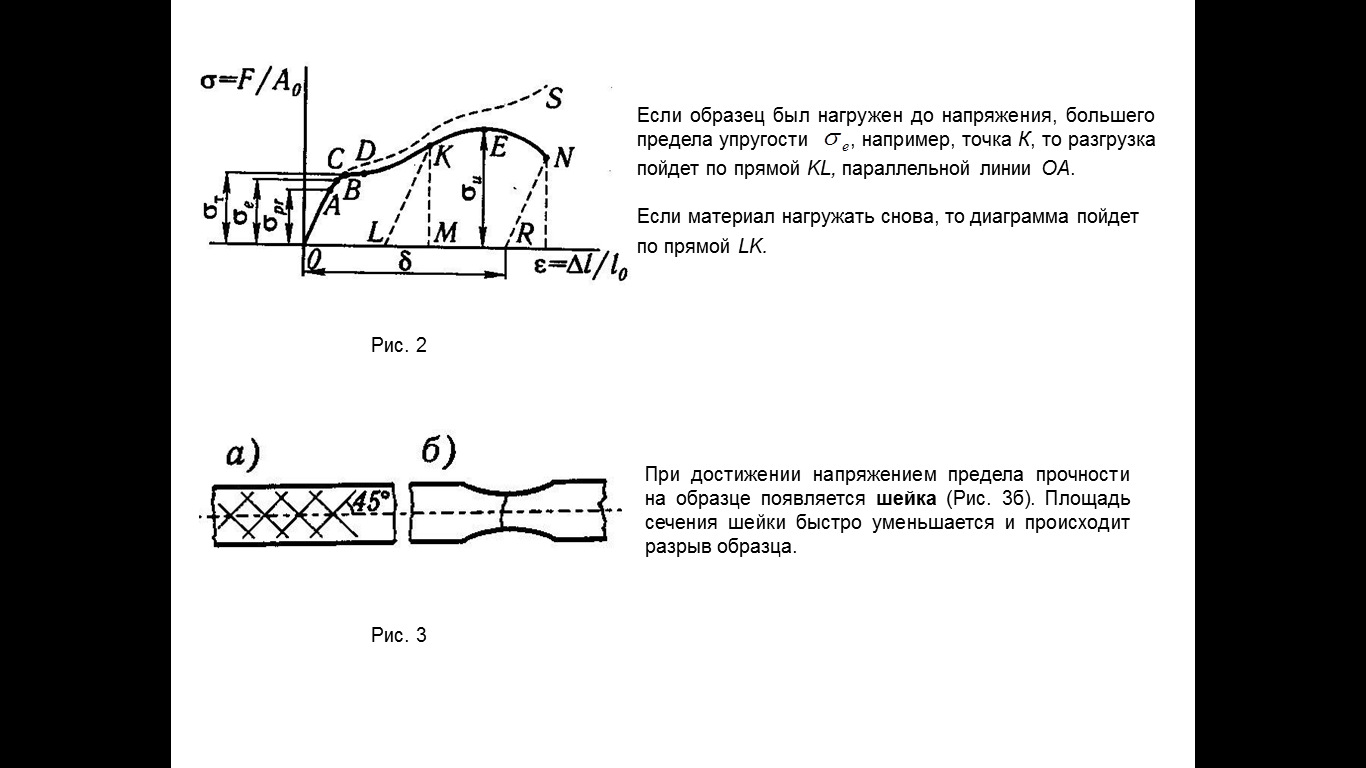

Основные типы задач при расчете на прочность растянутых ( сжатых стержней).

5.Сдвиг. Напряженное состояние и деформация при чистом сдвиге. Практич. Расчеты на сдвиг.
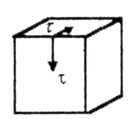
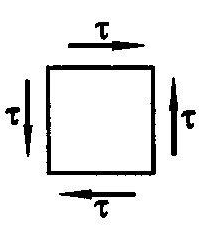
Если на гранях элемента действуют только касательные напряжения (Рис. 1), то такой вид напряженного состояния называется чистым сдвигом.
![]()
![]()
![]() -
угловая
деформация
или угол
сдвига,
где
- касательное напряжение, G
-
модуль сдвига (модуль упругости второго
рода). Формула (1) выражает закон
Гука при сдвиге.
-
угловая
деформация
или угол
сдвига,
где
- касательное напряжение, G
-
модуль сдвига (модуль упругости второго
рода). Формула (1) выражает закон
Гука при сдвиге.
![]()
![]()
![]() Тогда
,
Тогда
,
![]()
Практические расчеты на сдвиг. Q - поперечная сила в каждой заклепке, n - количество заклепок, F - внешняя растягивающая сила.
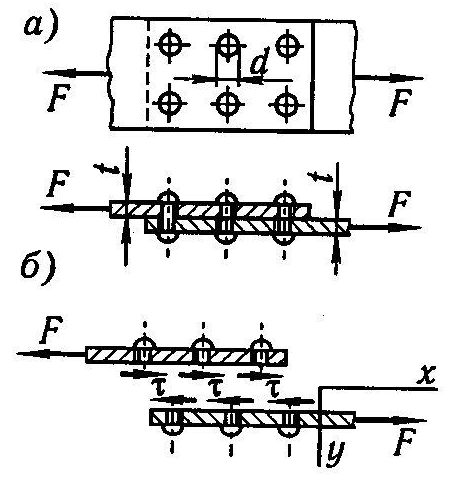
На рис. а показано соединение двух листов заклепками.
На рис. б показано разрушение соединения в результате среза заклепок
С![]()
![]() оставим
уравнение равновесия отсеченной части
соединения (Рис. б):
оставим
уравнение равновесия отсеченной части
соединения (Рис. б):
![]()
![]()
где A= πd2/4 - площадь сечения заклепки диаметром d.
![]()
У![]() словие
прочности
заклепок на срез имеет вид:
словие
прочности
заклепок на срез имеет вид:
г![]()
![]() де
-
допускаемое касательное напряжение на
срез
де
-
допускаемое касательное напряжение на
срез
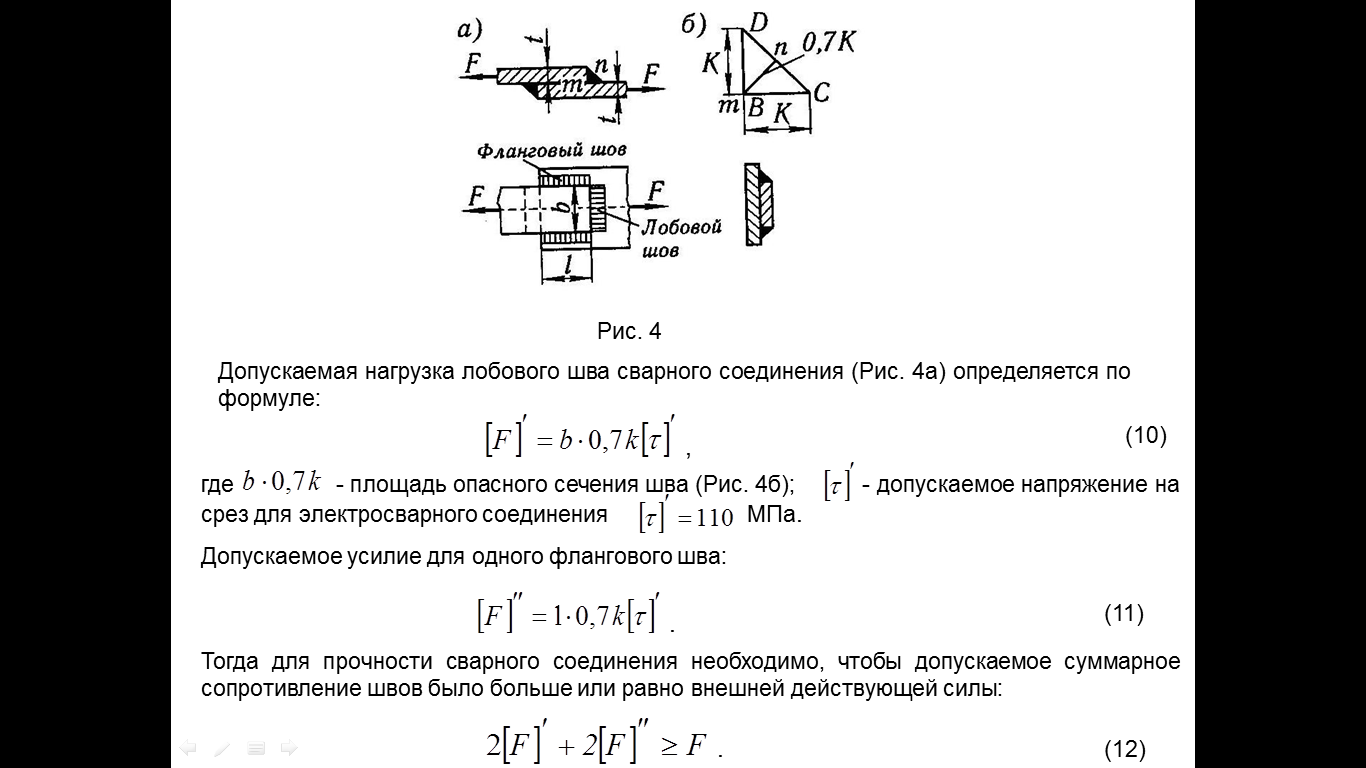
где - допускаемое напряжение на растяжение.
Геометрические харак-ки сечения. Изменение моментов инерции при парал-ном переносе и повороте осей.
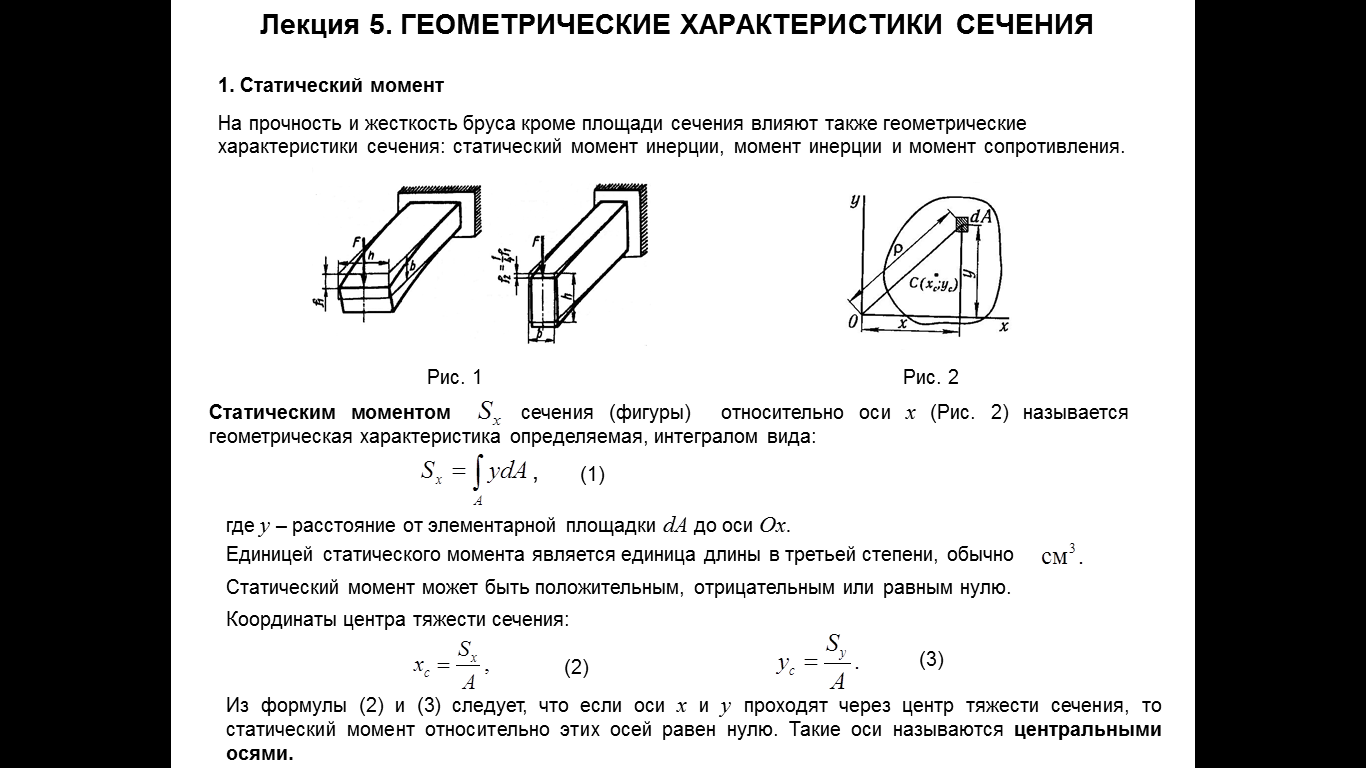
Зависимость между моментами инерции относительно парал-х осей.
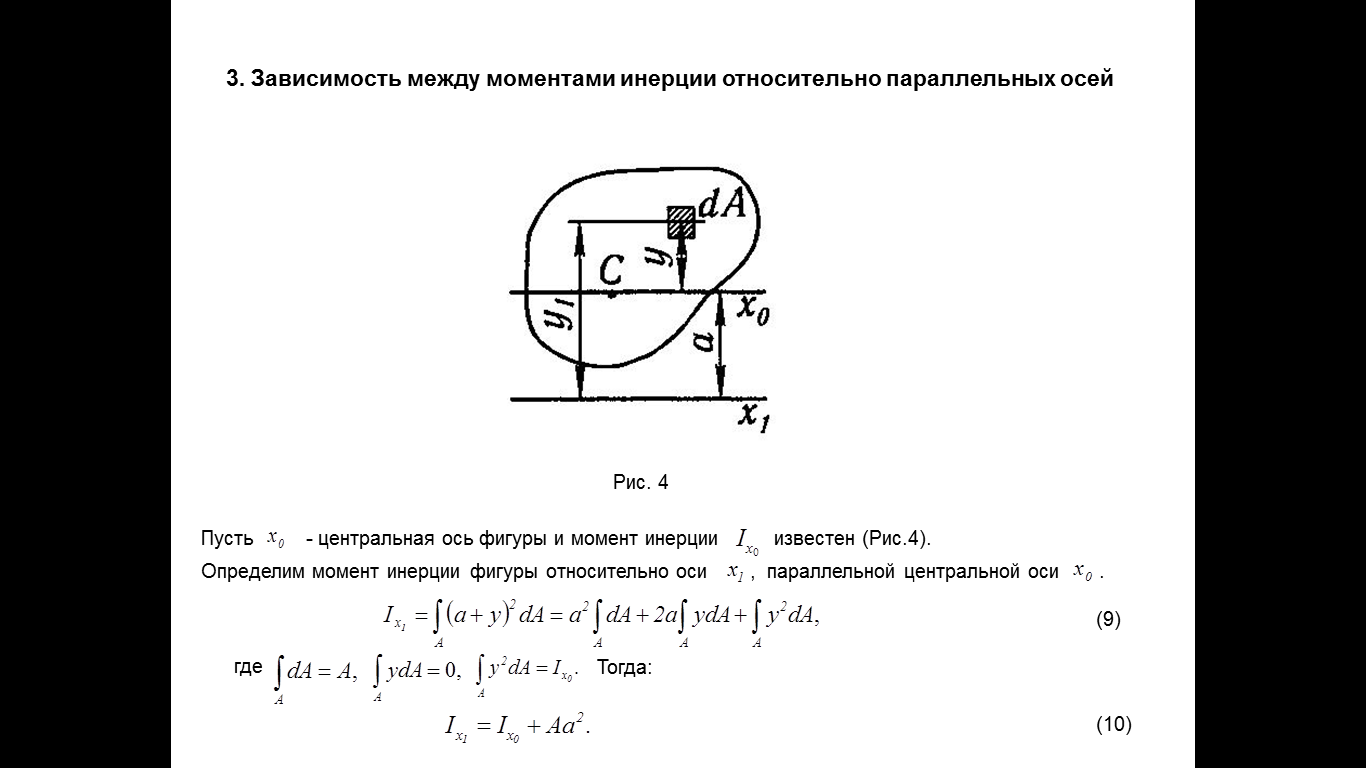
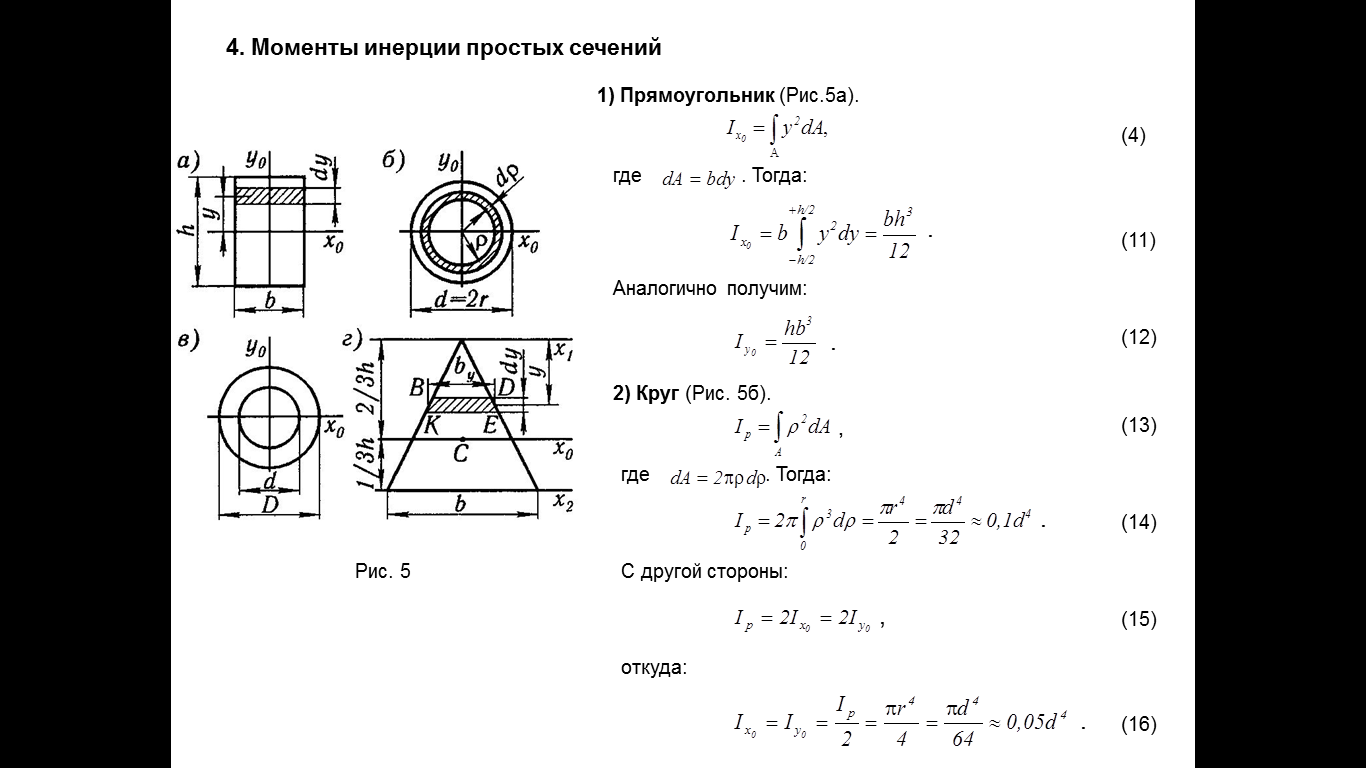
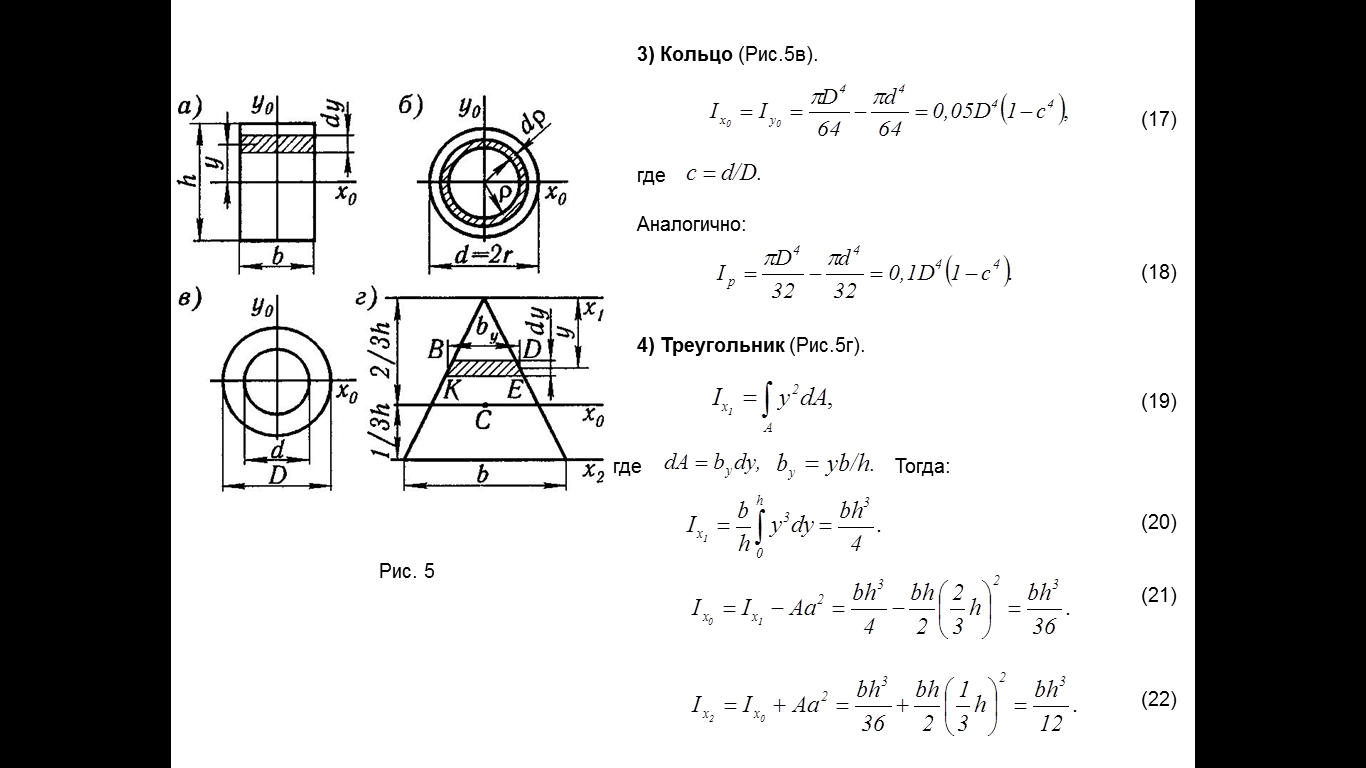
Изменение момента инерции при повороте осей.

7.Кручение. Определение напряжений и деформаций при кручении вала.
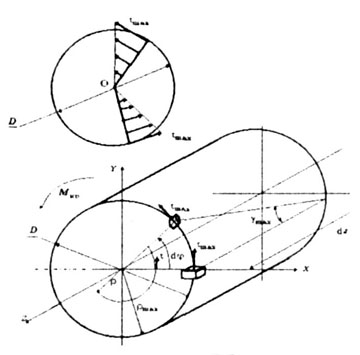
Кручением называется такой вид деформации, при котором в поперечном сечении вала возникает только крутящий момент Мкр, а все остальные внутренние силовые факторы равны нулю. |
Уравнение равновесия: |
|
Деформация - угол сдвига (рис, 3.2) |
|
Напряжения |
|
|
D - диаметр стержня круглого поперечного сечения, |
|
Угол закручивания элемента |
|
Угол закручивания стержня |
|
Напряженное состояние - чистый сдвиг (рис.3.1). |
|
Рис. 3.1 |
|
Рис. 3.2 |
Условие прочности: |
|
Для хрупких материалов: |
|
Для пластических материалов: |
|
Условие жесткости: |
|
8.Изгиб. Определение внутренних усилий при изгибе. Зависимость между изгибающим моментом, поперечной силой и интенсивностью распред. Нагрузки.

Деформация, при которой в поперечных сечениях возникают изгибающие моменты, называется изгибом. Изгибающим моментом называется момент, плоскость действия которого перпендикулярна плоскости поперечного сечения стержня.
Изгиб называется чистым, если изгибающий момент является единственным внутренним усилием, возникающим в сечении стержня.
Если в поперечных сечениях стержня наряду с изгибающими моментами возникают также и поперечные силы, то такой изгиб называется поперечным.
Если плоскость действия изгибающего момента (силовая плоскость) проходит через одну из главных центральных осей, то такой изгиб называется прямым или простым или плоским изгибом.
Если плоскость действия изгибающего момента в сечении не совпадает ни с одной из главных осей сечения, то такой изгиб называется косым.
Определение внутренних усилий при изгибе:




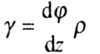
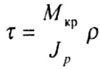
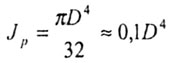 -
полярный момент инерции;
-
полярный момент инерции;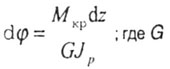 -
модуль упругости второго рода
-
модуль упругости второго рода