Полигон, гистограмма, кумулята

Для графического изображения вариационных рядов наиболее часто используются полигон, гистограмма, кумулята (кумулятная кривая).

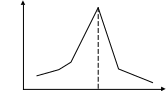
ОПР. Полигоном частот называют ломаную, отрезки которой соединяют точки (х₁, п₁), (х₂, п₂), ..., (х_k; п_k). Для по­строения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат — соответствующие им частоты п_i. Точки (х_i; п_i) соединяют отрезками прямых и получают полигон частот.

Полигон, как правило, служит для изображения дискретного ряда.

Гистограмма служит для изображения интервального ряда.

ОПР. Гистограммой частот называют ступен­чатую фигуру, состоящую из прямоугольников, основаниями кото­рых служат частичные интервалы длиною h, а высоты равны отноше­нию п_i /h (плотность ча­стоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии п_i /h.

Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.

ОПР. Кумулята – кривая накопленных частот.

Пример.

По данным примера 1 построим гистограмму, полигон, кумуляту.

Изобразим графически интервальный вариационный ряд.

На оси абсцисс отложим интервалы значений признака, а на оси ординат – соответствующие частоты, и построим прямоугольники с основаниями, равными длине интервала, и высотами, равными частоте. Полученная ступенчатая фигура является гистограммой распределения для вариационного ряда.

х

По гистограмме оценивают моду – mod x - варианта, которой соответствует наибольшая частота. По гистограмме это абсцисса точки пересечения прямых, соединяющих углы самого высокого столбца гистограммы с ближайшими углами соседних столбцов. В нашем примере М₀=13,4.

Полигон относительных частот лучше строить по дискретному вариационному ряду.

Если построить точки с координатами (х_i; ) и соединить их отрезками, то получим так называемый полигон относительных частот.

Если же построить точки с координатами (х_i; W_i) и соединим их отрезками, то получим график, который называется кумулятой.

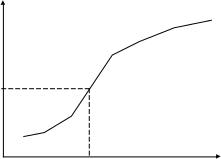
Опр. Медианой med x вариационного ряда называется варианта, которая делит вариационный ряд на две части, равные по числу вариант. Её удобнее находить по графику кумуляты – абсцисса точки ордината которой равна 0,5. Видно, что М_е=13,2.

Эмперическая функция распределения

Пусть нам известно статистическое распределение выборки. Обозначим через n_x – число наблюдений, при которых значения вариант оказываются меньше, чем х; п—общее число наблюдений (объем выборки). Ясно, что относительная частота события Х < х равна п_x/п. Если х изменяется, то, вообще говоря, из­меняется и относительная частота, т. е. относительная частота п_x/п есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

ОПР. Эмпирической функцией распределения (функцией рас­пределения выборки) называют функцию F* (х), опреде­ляющую для каждого значения х относительную частоту события Х < х.

Итак, по определению,

, (1)

где n_x — число вариант, меньших х; п — объем выборки. В отличие от эмпирической функции распределения выборки функцию распределения F(х) генеральной сово­купности называют теоретической функцией распределения. Различие между эмпирической и теоретической функ­циями состоит в том, что теоретическая функция F(х) определяет вероятность события Х < х, а эмпирическая функция F* (х) определяет относительную частоту этого же события. При больших п числа F* {х) и F (х) мало отли­чаются друг от друга. Поэтому F* {х) используют для приближенного представления теоре­тической (интегральной) функции распределения гене­ральной совокупности.

Такое заключение подтверждается и тем, что F* (х) обладает всеми свойствами F (х):

1. 0≤ F* {х) ≤1;

2. F* {х) – неубывающая функция;

3) если х₁—наименьшая варианта, то F*(х)=0 при x  x₁, если х_k,—наибольшая варианта, то F*(х)=1 при х > х_k.

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.