Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось п₁ раз, х₂ – п₂ раз, раз и , х_k – п_k раз и —объем выборки. Наблюдаемые значения х_i, называют вариантами, а последовательность вариант, записанных в возрастающем порядке,— вариа­ционным рядом. Числа наблюдений называют частотами , а их отношения к объему выборки - относи­тельными частотами.

ОПР. Статистическим распределением выборки называют пе­речень вариант и соответствующих им частот или относительных частот.

.

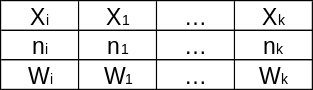
Статистическое распределение можно за­дать также в виде последовательности интервалов и соответ­ствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математи­ческой статистике—соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.

ОПР. Вариационный ряд называется дискретным, если любые варианты отличаются на постоянную величину, и – непрерывным (интервальным), если варианты могут отличаться друг от друга на сколь угодно малую величину.

Пример 1.

Пусть в результате эксперимента получены значения наружного диаметра гайки в мм:

13,21	14,51	12,01	13,42	13,61	14,02	12,12	13,22	13,66	13,43
13,88	13,32	13,82	13,49	12,48	13,26	13,58	13,81	13,84	13,31
13,55	12,32	12,38	13,24	13,46	13,73	14,18	13,7	13,45	13,23
13,41	13,52	13,58	12,87	13,01	13,3	13,36	14,45	14,13	13,53
13,53	12,78	13,59	13,54	14,21	13,41	12,42	13,47	13,3	14,37
13,13	13,67	13,25	13,48	13,25	12,59	14,15	13,44	12,3	13,22
13,5	14,26	12,6	13,27	13,29	13,35	12,96	13,51	13,55	13,5
12,61	12,9	14,27	12,88	13,33	13,57	13,38	13,56	13,4	13,1
13,4	13,93	13,16	13,34	13	12,72	13,12	13,39	13,19	13,99
13,18	13,28	13,8	13,39	13,78	13,85	13,9	13,94	13,27	14,79

Построим интервальный вариационный ряд.

N=100.

По таблице зарегистрированных в опыте значений признака находим наименьшее х_min и наибольшее х_max значение. Разность х_max - х_min=R называется размахом варьирования. Множество (х_min, х_max) разбиваем на l интервалов, называется шагом разбиения. Число интервалов берут равным l=1+ , n – объем выборки. После того, как построены интервалы, нужно для каждого интервала указать число n_i, попавших в него элементов выборки. Если результат измерения оказался на границе интервала, то будем относить его к левому интервалу.

Просматривая приведенные значения признака, выбираем х_min=12,01 и х_max=14,79. Эти граничные значения лучше округлить, тогда все значения признака будут находится в интервале (12,0; 14,8). R=14,8 – 12,0=2,8. После такого округления интервал удобнее разбить на частичные интервалы. Возьмем l=1+ 7,77, тогда .

Получим 7 частичных интервалов: 12,0 -12,4; 12,4 -12,8; 12,8 -13,2; 13,2 -13,6; 13,6 -14,0; 14,0 -14,4; 14,4 -14,8. Подсчитаем число значений признака (n_i), попавших в каждый частичный интервал. Полученный таким способом ряд запишется в виде таблицы:

интервалы	12,0-12,4	12,4-12,8	12,8-12,32	13,2-13,6	13,6-14,0	14,0-14,4	14,4-14,8
ni	5	7	14	50	13	8	3

Проварка: .

Построили интервальный вариационный ряд.

Строим дискретный вариационный ряд.

В качестве вариант х_i примем середины частичных интервалов. Например, для первого интервала 12,0 -12,4 варианта х_i=12,2. Составим статистический ряд распределения: в первой строке записываем все варианты х_i, во второй – соответствующие им частоты n_i; в третьей – подсчитанную относительную частоту , и в четвертой – накопленные относительные частоты W_i. Накопленная относительная частота для каждого интервала находится последовательным суммированием частот всех предшествующих интервалов, включая данный.

хi	12,2	12,6	13	13,4	13,8	14,2	14,6
ni	5	7	14	50	13	8	3
wi	0,05	0,07	0,14	0,5	0,13	0,08	0,03
Wi	0,05	0,12	0,26	0,76	0,89	0,97	1

Построили дискретный вариационный ряд.