Серия 23. Прочная?

1. Камиль задумал пятизначное число, кратное 9, и посчитал сумму его цифр. Потом он проделал эту же операцию с полученным числом. Какое число получил в результате Камиль?

2. Существует ли прочное разбиение полоски 3100 на доминошки?

3. Есть 10 монет, одна из которых – фальшивая. Имеется также детектор, который за одну операцию исследует 4 монеты и указывает на одну из них. Известно, что если среди исследуемых монет есть фальшивая, то детектор указывает на неё. Однако если фальшивой монеты среди исследуемых нет, то детектор может указать на любую монету. За какое наименьшее число операций удастся заведомо определить фальшивую монету?

4. Существует ли прочное разбиение прямоуольника 68 на доминошки?

5. На дистанции в 2 мили жираф обгоняет носорога на 1/4 мили, а носорог гиппопотама — на 1/8 мили. На сколько жираф обгонит гиппопотама на дистанции 2 мили?

6. Существует ли прочное разбиение квадрата 66 на доминошки?

7. Назовем трехзначное число “горкой”, если в нем цифра в разряде десятков больше любой из двух оставшихся, и “ямкой”, если в нем цифра в разряде десятков меньше любой из двух оставшихся. Каких чисел больше – “горок” или “ямок”, и на сколько?

8. Существует ли прочное разбиение полоски 4100 на доминошки?

9. Может ли число, записываемое при помощи 100 нулей, 100 единиц и 100 двоек, быть точным квадратом?

10. Есть 100 монет, одна из которых – фальшивая. За какое наименьшее число операций удастся с помощью детектора из задачи 3 заведомо определить фальшивую монету?

Серия 24. Инвариантная.

1. На сосне растут 8 бананов и 7 апельсинов. Если сорвать два 23одинаковых фрукта, то на сосне тут же вырастет один банан, а если сорвать два разных – вырастет один апельсин. Срывать фрукты по одному нельзя. Можно ли сорвать фрукты с сосны так, чтобы последним был банан?

2. Черный ящик работает так: любые три числа a, b и c, попадающие в него, он перерабатывает в числа a+b–c, b+c–a, c+a–b. Можно ли с помощью этого ящика из чисел 1, 3, 9 получить числа –11111111113, 3, 11111111111?

3. На доске написаны числа от 1 до 100. Разрешается стереть любые два числа и написать вместо них их разность. Может ли после 99 таких операций остаться число 1?

4. На нижней половине доски 10x10 стоят шашки (50 шт.) Разрешается перепрыгнуть шашкой через соседнюю с ней, если следующая клетка свободна. Можно ли собрать все шашки на верхней половине доски?

5. В одной вершине куба написано число 1, в остальных — нули. Можно прибавлять по единице к числам в концах любого ребра. Можно ли добиться, чтобы все числа делились на 3?

6. Можно ли операциями «умножить на 7» и «прибавить 6» получить из единицы число 2006?

7. Есть куча из 1001 камня. Ход состоит в том, что из какой-нибудь кучи, где лежит более одного камня, выкидывают один камень на помойку, а затем любую кучу делят на две произвольные части. Можно ли через неско.лько ходов получить лишь кучи, состоящие из трех камней?

8. На доске написано целое число, большее 1. Разрешённые операции: если на доске уже есть число A, можно дописать ещё числа 2A и 3A.

   1. Докажите, что сумма чисел на доске всегда будет составной.

   2. Можно ли получить несколько чисел с общей суммой 2007?

Серия 25. Числа-числа!

И все такие разные…

1. Что больше:

1. 50⁵⁰ или 216³³?

2. 2⁶⁵ или 3⁵⁶?

3. 6⁶⁵ или 9⁵⁶?

2. Известно, что a³ делится на 1620. Укажите максимальное натуральное число, на которое наверняка делится a

3. Найдите все натуральные числа, в 12 раз большие своей суммы цифр.

4. Докажите, что число 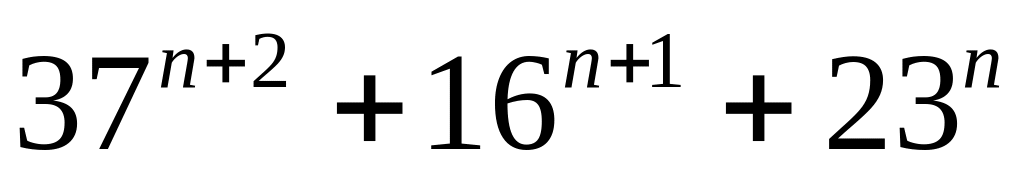делится на 7 для любого натурального n

5. Решите в натуральных числах уравнение

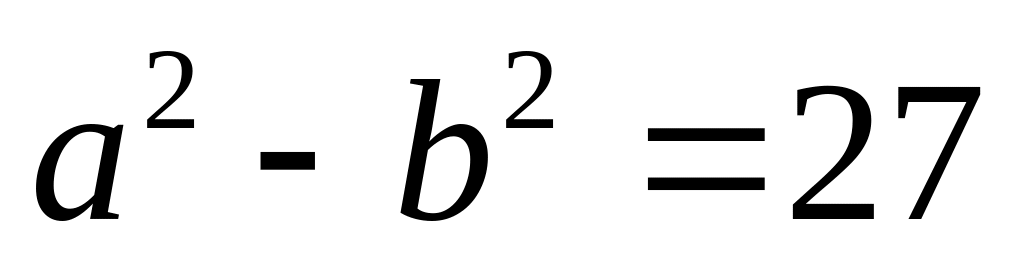
6. Все простые числа, не превосходящие простого числа р, разбили на две группы и нашли произведение всех чисел в каждой из групп, после чего из большего произведения вычли меньшее. Эта разность оказалась меньше р. Докажите, что она равна 1.

7. Найдите сумму: .

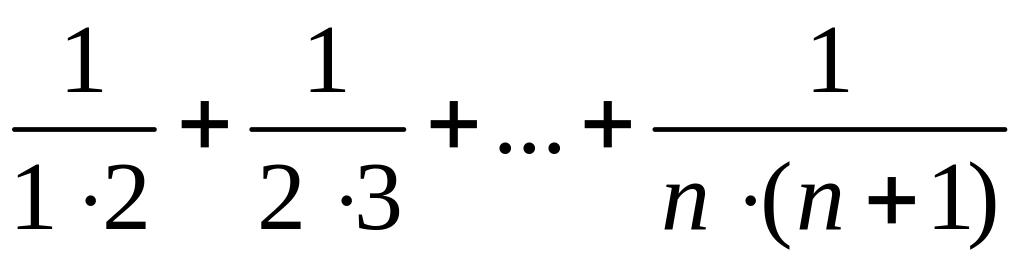8. а, b и c ‑ натуральные числа такие, что а³ делится на b, b³ делится на c, а c³ делится на a. Докажите, что (a+b+c)¹³ делится на abc.

Серия 26. С Днем рождения Макар!

Ура! Игротека!!!

1. Шоколадка представляет собой прямоугольник 5 × 8, разделённый бороздками на 40 квадратиков. Макар и Саша по очереди разламывают её на части по бороздкам: за один ход можно разломить любой из кусков на два. Макар ходит первым, кто не может сделать хода – проигрывает. Кто выигрывает при правильной игре?

2. Двое играют, поочередно выставляя крестики и нолики на квадратном поле 9 9. В конце каждый получает очко за каждую строку и столбец, в которых его знаков больше. Кто выигрывает при правильной игре?

3. Игра начинается с числа 30. За ход можно уменьшить число на любой из его делителей. Проигрывает тот, кто получит 0. Кто выигрывает при правильной игре?

4. Двое играют в следующую игру: первый выбирает любое поле на доске 8×8 и ставит туда коня. Дальше они по очереди, начиная со второго делают ход при условии, что на эту клетку раньше никто не вставал. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

5. Соня и Полина играют в такую игру: имеется доска 100100. Соня каждым ходом закрашивает одну клетку, а Полина – уголок из трёх клеток. Соня ходит первой. Кто выиграет при правильной игре?

6. На столе лежит куча из 2011 монет. Сеня и Макар по очереди берут монеты из кучи. Начинает Сеня. За один ход можно брать одну или две монеты. Игра заканчивается, когда все монеты из кучи взяты. Выигрывает тот, у кого на руках по окончании игры окажется нечетное число монет. Кто выиграет при правильной игре?

7. У прямоугольной доски 10×11 выпилили все внутренние клетки так, что получилась рамка шириной в одну клетку. Разрешается вырезать любой прямоугольник 1×п так, чтобы оставшаяся фигура не развалилась на 2 части. Тот, кто не может сделать ход, – проигрывает. Макар выбирает, первым или вторым он будет ходить. Помогите ему.

8. В музее 100 картин. Двое смотрителей дежурят по очереди. В свое дежурство смотритель переворачивает ровно 5 картин (у каждой картины есть ровно 2 положения). Проигрывает тот, после чьего хода ситуация повторится. Кто выигрывает при правильной игре и как ему для этого играть?