2.4.1. Метод простой скользящей средней.

Сначала для временного ряда: определяется интервал сглаживания . Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности большим; интервал сглаживания уменьшают, если нужно сохранить более мелкие колебания.

При прочих равных условиях интервал сглаживания рекомендуется брать нечетным.

Для первых уровней ряда вычисляется их среднее арифметическое. Это будет сглаженное значение уровня ряда, находящегося в середине интервала сглаживания. Затем интервал сглаживания сдвигается на один уровень вправо, повторяется вычисление среднего арифметического и так далее. Для вычисления сглаженных уровней ряда применяется формула:

где (при нечетном ); для четных формула усложняется.

В результате такой процедуры получаются сглаженных значений уровней ряда; при этом первые и последние уровней ряда теряются (не сглаживаются). Другой недостаток метода в том, что он применим лишь для рядов, имеющих линейную тенденцию.

2.4.2. Метод взвешенной скользящей средней.

Метод взвешенной скользящей средней отличается от предыдущего метода сглаживания тем, что уровни, входящие в интервал сглаживания, суммируются с разными весами. Это связано с тем, что аппроксимация ряда в пределах интервала сглаживания осуществляется с использованием полинома не первой степени, как в предыдущем случае, а степени начиная со второй.

Используется формула средней арифметической взвешенной:

,

причем веса определяются с помощью метода наименьших квадратов. Эти веса рассчитаны для различных степеней аппроксимирующего полинома и различных интервалов сглаживания.

1. для полиномов второго и третьего порядков числовая последовательность весов при интервале сглаживания имеет вид: , а при 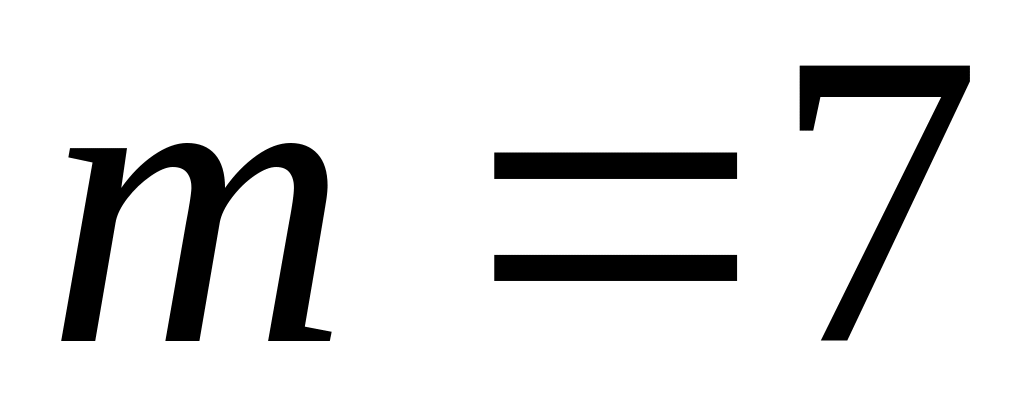имеет вид: ;

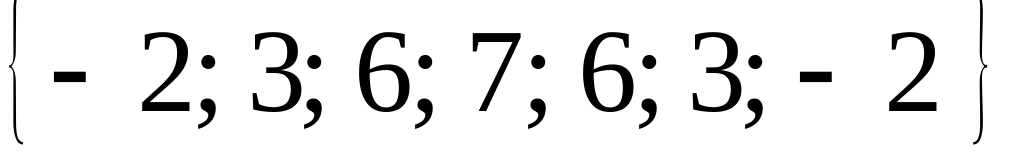2. для полиномов четвертой и пятой степеней и при интервале сглаживания последовательность весов выглядит следующим образом: .

Распределение весов на протяжении интервала сглаживания, полученное на основе метода наименьших квадратов см. на диаграмме 1.

Диаграмма 1. Распределение весов.

2.4.3. Метод экспоненциального сглаживания.

К той же группе методов относится метод экспоненциального сглаживания.

Его особенность заключается в том, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное значение уровня ряда.

Если для исходного временного ряда

соответствующие сглаженные значения обозначить через , то экспоненциальное сглаживание осуществляется по формуле:

, (4)

где параметр сглаживания ; величина называется коэффициентом дисконтирования.

Используя, приведенное рекуррентное соотношение для всех уровней ряда, начиная с первого и кончая моментом времени , можно получить, что экспоненциальная средняя, то есть сглаженное данным методом значение уровня ряда, является взвешенной средней всех предшествующих уровней:

;

здесь величина, характеризующая начальные условия.

В практических задачах обработки экономических временных рядов рекомендуется выбирать величину параметра сглаживания в интервале от 0,1 до 0,3. Других точных рекомендаций для выбора оптимальной величины параметра нет. В отдельных случаях предлагается [1] определять величину исходя из длины сглаживаемого ряда:

.

Что касается начального параметра , то в конкретных задачах его берут или равным значению первого уровня ряда , или равным среднему арифметическому нескольких первых членов ряда, например, элементов :

.

Указанный выше порядок выбора величины обеспечивает хорошее согласование сглаженного и исходного рядов для первых уровней. Заметим, что метод сглаживания не теряет ни начальные, ни конечные уровни ряда.