Теория вероятностей Дискретные случайные величины

325. Задание {{ 34 }} Дисс_№1

Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

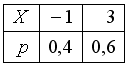
Тогда математическое ожидание этой случайной величины равно…

 1,4

 1,8

 2,2

 1

326. Задание {{ 35 }} Дисс_№2

Дан закон распределения вероятностей дискретной случайной величины X:

X	1	2	3	4
P	0,2	0,3	0,4	a

Тогда значение а равно ...

 0,1

 0,5

 0,7

 0,4

327. Задание {{ 104 }} Дисс_№3

Пусть X и Y - независимые дискретные случайные величины, причем MX=2, MY=-3, Z=5X-3Y+2. Тогда MZ равно ...

Правильные варианты ответа: 21;

328. Задание {{ 105 }} Дисс_№4

Пусть X и Y - независимые дискретные случайные величины, причем DX=2, DY=9, Z=5X-3Y+2. Тогда DZ равно ...

Правильные варианты ответа: 131;

329. Задание {{ 106 }} Дисс_№5

Дискретная случайная величина X имеет биномиальное распределение, если она принимает значение 0,1,2,3…,n, с вероятностями (где 0<p<1,q=1-p,m=0,1,..n)









330. Задание {{ 107 }} Дисс_№6

Дискретная случайная величина X имеет распределение Пуассона, если ее возможные значения: 0,1,2, …, m, … (счетное множество значений), а соответствующие вероятности выражаются формулой Пуассона (где m=0,1,2,…,a – параметр)









331. Задание {{ 108 }} Дисс_№7

В лотерее имеется 1000 билетов, из них выигрышных: 10 по 500 руб, 50 по 50 руб, 100 по 10 руб, 150 по 1 руб. Математическое ожидание выигрыша на один билет равно ...

 8

 9

 8,65

 8,55

332. Задание {{ 109 }} Дисс_№8

Дискретная случайная величина X задана рядом распределения:

X	-1	0	1	2
p	0,2	0,1	0,3	0,4

DX равна …

 2

 1

 1,19

 1,29

333. Задание {{ 110 }} Дисс_№9

Дискретная случайная величина X задана рядом распределения:

X	-1	0	1	2
p	0,2	0,1	0,3	0,4

равна …

 1

 2

 1,14

 1,5

334. Задание {{ 111 }} Дисс_№10

Дискретная случайная величина X имеет геометрическое распределение, если ее возможные значения: 1,2,3,4,…, а вероятности этих значений (где m=1,2,3,…)









335. Задание {{ 123 }} Дисс_№11

Дискретная случайная величина Х задана законом распределения вероятностей.

Пусть  – математическое ожидание. Тогда    равно …

Правильные варианты ответа: 2,5;

336. Задание {{ 126 }} Дисс_№12

Дискретная случайная величина Х задана законом распределения вероятностей 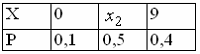Если математическое ожидание , то значение  равно …

 3

 4

 5

 6

337. Задание {{ 166 }} Дисс_№13









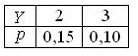
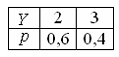
338. Задание {{ 194 }} Дисс_№14









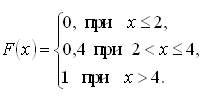
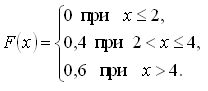
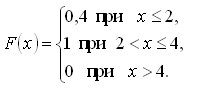
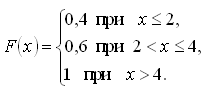
339. Задание {{ 196 }} Дисс_№15







