13.Манометрическое и вакуумное давление.

В открытых сосудах, водоемах абсолютным давлением окружающей среды является атмосферное давление р_а. Для этих случаев р=р_а+ρgh.

Если абс давление в данной точке жидкости больше атмосферного(р>р_а), то ρgh=p_м=p-p_a.

Манометрическое давление представляет собой избыток давления в данной точке над атмосерным.

Из предыдущего уравнения можно определить пределы изменения p_м:р=р_а , р_м=0, при р→∞, р_м→∞, т.е. значение р_м изменяется от 0 до ∞.

Если абсолютное давление в данной точке жидкости меньше атмосферного(р<р_а), то ρgh определяет вакуум, или разряжение,

Р_в=ρhg=p_a-p.

Вакуум представляет собой недостаток давления в данной точке, до атмосферного.

Пределы изменения вакуума могут быть установлены из предыдущего выражения: р→0, р_в→р_а, при р=р_а, р_в=0, т.е. значение вакуума может меняться от 0 до р_а.

14. Сообщающиеся сосуды

Закон сообщающихся сосудов — один из законов гидростатики, гласящий, что в сообщающихся сосудах уровни однородных жидкостей, считая от наиболее близкой к поверхности земли точки, равны.

Рассмотрим два сообщающихся сосуда, в которых находится жидкость плотностью . Давление жидкости в I сосуде расписывается по формуле , где  — высота столба в I сосуде. Давление жидкости во II сосуде расписывается аналогично как , где  — высота столба во II сосуде. Так как система статична, то давления равны, и , ч. т. д.

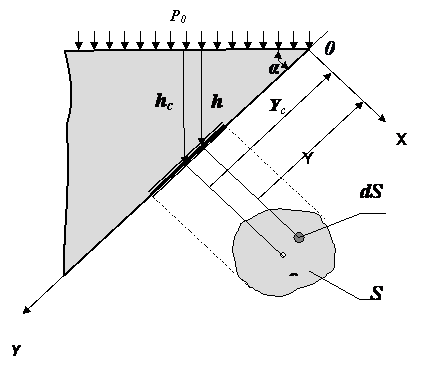
15. Сила давления жидкости на плоскую стенку

• 

Рассмотрим произвольную площадку ds, расположенную на плоской наклонной стенке сосуда с жидкостью на расстоянии Y от оси X, и определим силы, действующие на эту площадку. Сила от давления, действующего на элементарную площадку dS, будет описываться формулой:

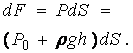
Если проинтегрировать это выражение по площади, можно определить полную силу, действующую на всю площадь целиком

Из рисунка ясно, что в последнем выражении . Подставив значение h в предыдущее выражение, будем иметь:

Из теоретической механики известно, что интеграл  есть ни что иное, как статический момент площади Sотносительно оси 0X. Он равен произведению этой площади на координату её центра тяжести, т.е. можно записать

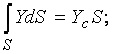
где Yс – расстояние от оси X до центра тяжести площади S.

Подставив формулу момента в выражение силы, получим:

Анализ второго слагаемого показывает, что произведение  это глубина положения центра тяжести площадки, а  - избыточное давление жидкости в центре тяжести площадки. С учётом этого можно записать

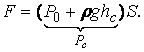
Сумма в скобках в последнем выражении является абсолютным давлением в центре тяжести рассматриваемой произвольной площадки. Таким образом, можно сделать вывод: полная сила давления жидкости на плоскую стенку равна произведению её площади на величину гидростатического давления в центре тяжести этой стенки.

Однако необходимо учесть, что эта сила не сконцентрирована в точке, а распределена по площади. И распределение это неравномерно. По этой причине для расчётов, кроме величины силы действующей на наклонную площадку, необходимо знать точку приложения равнодействующей.