44. Коэффициент Дарси

Формула Вейсбаха^[1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом (англ.) в 1855 году):

где

• Δh — потери напора на гидравлическом сопротивлении;

• ξ — коэффициент потерь (коэффициент Дарси);

• V — средняя скорость течения жидкости;

• g — ускорение свободного падения;

• величина называется скоростным (или динамическим) напором.

Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:

где

ΔP — потери давления на гидравлическом сопротивлении;

ρ — плотность жидкости.

Формула Дарси — Вейсбаха

Если гидравлическое сопротивление представляет собой участок трубы длиной L и диаметром D, то коэффициент Дарси определяется следующим образом:

где λ — коэффициент потерь на трение по длине.

Тогда формула Дарси приобретает вид:

или для потери давления:

Последние две зависимости получили название формулы Дарси — Вейсбаха^[2]. Предложена Л. Ю. Вейсбахом (L. J. Weisbach, 1845) и А. Дарси (1857).

Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D представляет собой гидравлический диаметр.

Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.

[Править] Определение коэффициента потерь на трение по длине

Коэффициент λ определяется по разному для разных случаев.

Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:

где Re — число Рейнольдса.

Иногда для гибких труб в расчётах принимают

Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:

Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса Re_кр до значений Re = 10⁵. Формула Блазиуса применяется для гидравлически гладких труб.

Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).

[Править] Определение коэффициента Дарси для местных сопротивлений

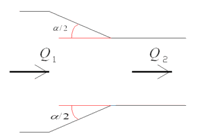
Рис. 1. Гидравлический конфузор: Q₁ — поток жидкости в широком сечении трубы; Q₂ — поток жидкости в узком сечении трубы

Для каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента ξ.

К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.

1. При внезапном расширении трубы:

где S₁ и S₂ — площади поперечного сечения трубы, соответственно перед расширением и после него.

2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:

Рис. 2. Зависимость коэффициента Дарси от угла δ поворота трубы

где S₁ и S₂ — площади поперечного сечения трубы, соответственно, перед сужением и после него.

3. При постепенном сужении трубы (конфузор):

,

где  — степень сужения; λ_T — коэффициент потерь на трение по длине при турбулентном режиме.

4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).